digital root问题
问题阐述会是这样的:
Given a non-negative integer num, repeatedly add all its digits until the result has only one digit.
For example:
Given num = 38, the process is like: 3 + 8 = 11, 1 + 1 = 2. Since 2 has only one digit, return it.
Follow up:
Could you do it without any loop/recursion in O(1) runtime?
这其实是一个digital root的问题。
digital root的定义如下:
The digital root (also repeated digital sum) of a non-negative integer is the (single digit) value obtained by an iterative process of summing digits, on each iteration using the result from the previous iteration to compute a digit sum. The process continues until a single-digit number is reached.
For example, the digital root of 65,536 is 7, because 6 + 5 + 5 + 3 + 6 = 25 and 2 + 5 = 7.
编程题中一般会要求在O(1)时间算出一个数的digital root,这时候就不能用上述思想解答问题了。
通用公式:
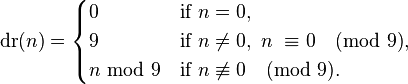 或者是
或者是
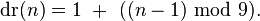
所有的原理其实和模运算以及同余定理有关:
考虑12345 = 1 × 10,000 + 2 × 1,000 + 3 × 100 + 4 × 10 + 5.
同时10 i= 9 + 1; 100 i= 99 + 1,所以又可以写成:
12,345 = 1 × (9,999 + 1) + 2 × (999 + 1) + 3 × (99 + 1) + 4 × (9 + 1) + 5.
展开后:
12,345 = (1 × 9,999 + 2 × 999 + 3 × 99 + 4 × 9) + (1 + 2 + 3 + 4 + 5).
这样便满足了数根的思想,计算数根的一次迭代,当然(1 + 2 + 3 + 4 + 5)=15 又可以接着迭代,总之是:

数根是模9的余数是因为 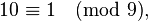 因此
因此 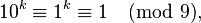 这样便有
这样便有 ,也就有如下推论:
,也就有如下推论:

这里要强调为什么当数字是9的倍数时,dr(n)是9?
例如:18 = 10 + 9
$18 \equiv 0 \pmod{9}$
但 $10 + 9 \equiv 1 + 8 \pmod{9}$,莫着急,这只是表象, $1 + 8 = 9 \equiv 0 \pmod{9}$
所以9的倍数的数根也可以用(mod 9)运算,只不过由于数根只在1-9之间,所以为零时只要换成9即可,毕竟$9 \equiv 0 \pmod{9}$
至于
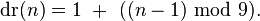 也是这个道理,数根只能在1-9之间,而(mod 9)的数域在0-8之间, 所以先对数字减1然后再补1即可折中等效了。
也是这个道理,数根只能在1-9之间,而(mod 9)的数域在0-8之间, 所以先对数字减1然后再补1即可折中等效了。
关键点是理解为什么由
$a = b + c$
$b \equiv r_1 \pmod{9} $
$c \equiv r_2 \pmod{9} $
可推导出:
$a \equiv r_1 + r_2\pmod{9}$
提示:把数写成 $n = mq + r $,依据一条推论:
推论 a≡b(mod m)的充要条件是a=mt+b(t为整数)。
表示对模m同余关系的式子叫做模m的同余式,简称同余。
参考资料:
A NEAT NUMBER TRICK: DIGITAL ROOTS AND MODULO-9 ARITHMETIC
digital root问题的更多相关文章
- Digital root(数根)
关于digital root可以参考维基百科,这里给出基本定义和性质. 一.定义 数字根(Digital Root)就是把一个数的各位数字相加,再将所得数的各位数字相加,直到所得数为一位数字为止.而这 ...
- 数字根(digital root)
来源:LeetCode 258 Add Dights Question:Given a non-negative integer num , repeatedly add all its digi ...
- 【HDOJ】4351 Digital root
digital root = n==0 ? 0 : n%9==0 ? 9:n%9;可以简单证明一下n = a0*n^0 + a1*n^1 + ... + ak * n^kn%9 = a0+a1+..+ ...
- Sum of Digits / Digital Root
Sum of Digits / Digital Root In this kata, you must create a digital root function. A digital root i ...
- 1. 数字根(Digital Root)
数字根(Digital Root)就是把一个自然数的各位数字相加,再将所得数的各位数字相加,直到所得数为一位数字为止.而这个一位数便是原来数字的数字根.例如: 198的数字根为9(1+9+8=18,1 ...
- 快速切题 sgu118. Digital Root 秦九韶公式
118. Digital Root time limit per test: 0.25 sec. memory limit per test: 4096 KB Let f(n) be a sum of ...
- Codeforces Beta Round #10 C. Digital Root 数学
C. Digital Root 题目连接: http://www.codeforces.com/contest/10/problem/C Description Not long ago Billy ...
- 数学 - SGU 118. Digital Root
Digital Root Problem's Link Mean: 定义f(n)为n各位数字之和,如果n是各位数,则n个数根是f(n),否则为f(n)的数根. 现在给出n个Ai,求出A1*A2*…*A ...
- 构造水题 Codeforces Round #206 (Div. 2) A. Vasya and Digital Root
题目传送门 /* 构造水题:对于0的多个位数的NO,对于位数太大的在后面补0,在9×k的范围内的平均的原则 */ #include <cstdio> #include <algori ...
随机推荐
- VS2013 编译错误 error: MSB8031
VS2010 创建的 MFC 程序,用 VS2013 打开后编译出现错误: C:\Program Files (x86)\MSBuild\Microsoft.Cpp\v4.0\V120\Microso ...
- mysql 命令
1.查看数据库: mysql> show databases; 2.使用数据库 mysql> use mysqldata; 3.查看数据表 mysql> show tables; 4 ...
- mutex 和 spinlock 对比
理论上: mutex和spinlock都是用于多进程/线程间访问公共资源时保持同步用的,只 是在lock失败的时候处理方式有所不同.首先,当一个thread 给一个mutex上锁失败的时候,threa ...
- 重读LPTHW-Lesson37
这次是复习课 复习python符号 整理如下 1.逻辑运算符not.and.or python中逻辑运算符包括not(布尔非).and(布尔与).or(布尔或).注意以下几点: ①运算规则: 例: ...
- 正式学习React(一) 开始学习之前必读
为什么要加这个必读!因为webpack本身是基于node环境的, 里面会涉及很多路径问题,我们可能对paths怎么写!webpack又是怎么找到这些paths的很迷惑. 本文是我已经写完正式学习Rea ...
- ui原则
http://www.niushe.com/news/show-3683.html 设计师Joshua Porter发表了一篇文章——<Principles of User Interface ...
- mysql数据损坏修复方法
1.myisamchk使用 myisamchk 必须暂时停止 MySQL 服务器.例如,我们要检修 discuz 数据库.执行以下操作:# service mysql stop (停止 MySQL ) ...
- 【HDU 4452 Running Rabbits】简单模拟
两只兔子Tom和Jerry在一个n*n的格子区域跑,分别起始于(1,1)和(n,n),有各自的速度speed(格/小时).初始方向dir(E.N.W.S)和左转周期turn(小时/次). 各自每小时往 ...
- linux ar 命令的使用
摘自http://blog.csdn.net/hxg130435477/article/details/8217247 用途说明 创建静态库.a文件.用C/C++开发程序时经常用到,但我很少单独在命令 ...
- hdu 5500 Reorder the Books(规律)
题意: 有一个1→n的排列形成的数列,我们要用最少的操作次数把这个数列从小到大排序,每次操作都是把一个数放到整个数列的最前面. 思路: 首先最大的数n是不用操作的(其他数操作好了,n ...
