cf500B New Year Permutation

B. New Year Permutation

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

User ainta has a permutation p₁, p₂, ..., p_n. As the New Year is coming, he wants to make his permutation as pretty as possible.

Permutation a₁, a₂, ..., a_n is prettier than permutation b₁, b₂, ..., b_n, if and only if there exists an integer k (1 ≤ k ≤ n) where a₁ = b₁, a₂ = b₂, ..., a_k - 1 = b_k - 1 and a_k < b_k all holds.

As known, permutation p is so sensitive that it could be only modified by swapping two distinct elements. But swapping two elements is harder than you think. Given an n × n binary matrixA, user ainta can swap the values of p_i and p_j (1 ≤ i, j ≤ n, i ≠ j) if and only if A_i, j = 1.

Given the permutation p and the matrix A, user ainta wants to know the prettiest permutation that he can obtain.

Input

The first line contains an integer n (1 ≤ n ≤ 300) — the size of the permutation p.

The second line contains n space-separated integers p₁, p₂, ..., p_n — the permutation p that user ainta has. Each integer between 1 and n occurs exactly once in the given permutation.

Next n lines describe the matrix A. The i-th line contains n characters '0' or '1' and describes the i-th row of A. The j-th character of the i-th line A_i, j is the element on the intersection of the i-th row and the j-th column of A. It is guaranteed that, for all integers i, j where 1 ≤ i < j ≤ n, A_i, j = A_j, i holds. Also, for all integers i where 1 ≤ i ≤ n, A_i, i = 0holds.

Output

In the first and only line, print n space-separated integers, describing the prettiest permutation that can be obtained.

Sample test(s)

Input

7
5 2 4 3 6 7 1
0001001
0000000
0000010
1000001
0000000
0010000
1001000

Output

1 2 4 3 6 7 5

Input

5
4 2 1 5 3
00100
00011
10010
01101
01010

Output

1 2 3 4 5

Note

In the first sample, the swap needed to obtain the prettiest permutation is: (p₁, p₇).

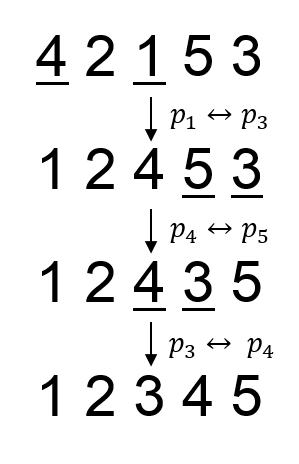
In the second sample, the swaps needed to obtain the prettiest permutation is (p₁, p₃), (p₄, p₅), (p₃, p₄).

A permutation p is a sequence of integers p₁, p₂, ..., p_n, consisting of n distinct positive integers, each of them doesn't exceed n. The i-th element of the permutation p is denoted as p_i. The size of the permutation p is denoted as n.

这题是给出交换矩阵，求交换完字典序最小

原来我是这样想的

n^2暴力枚举i<j,a[i]>a[j]的一对交换，换到最后没了就好了。这样每次至少减少1逆序对，做n次不就完了吗 恩才n^3可以接受

（阿连哭死在厕所）

妈蛋当时我到底在想什么……逆序对个数是n^2啊……要n^4不爆才怪

我们发现如果a[i]、a[j]可以互换，那么i和j是连通的。在同一联通块中的元素都是可以互换的

联通块可以直接用并查集或者floyd搞出来

然后从小到大枚举每一个位置，用它所在联通块中没取到的最小元素填进去

#include<cstdio>
#include<iostream>
#include<cstring>
#include<cstdlib>
#include<algorithm>
#include<cmath>
#include<set>
#include<map>
#include<ctime>
#include<iomanip>
#define LL long long
#define inf 0x7ffffff
#define N 200010
using namespace std;
inline LL read()
{
    LL x=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9'){if(ch=='-')f=-1;ch=getchar();}
    while(ch>='0'&&ch<='9'){x=x*10+ch-'0';ch=getchar();}
    return x*f;
}
int n;
int a[1010];
bool mrk[1010];
bool p[1010][1010];
int main()
{
	n=read();
	for (LL i=1;i<=n;i++)a[i]=read();
	for (int i=1;i<=n;i++)
	{
		char ch[1010];scanf("%s",ch+1);
		for (int j=1;j<=n;j++)
			if (ch[j]=='1')p[i][j]=1;
		p[i][i]=1;
	}
	for (int k=1;k<=n;k++)
		for (int i=1;i<=n;i++)
			for (int j=1;j<=n;j++)
				if(p[i][k]&&p[k][j])p[i][j]=1;
	memset(mrk,1,sizeof(mrk));
	for (int i=1;i<=n;i++)
	{
		int mn=inf,res=0;
		for (int j=1;j<=n;j++)
			if (mrk[j]&&p[i][j]&&a[j]<mn)
			{
				mn=a[j];
				res=j;
			}
		mrk[res]=0;
		printf("%d ",mn);
	}
	return 0;
}