zoj 2974 Just Pour the Water （矩阵快速幂，简单）

题目

对于案例的解释请见下图：

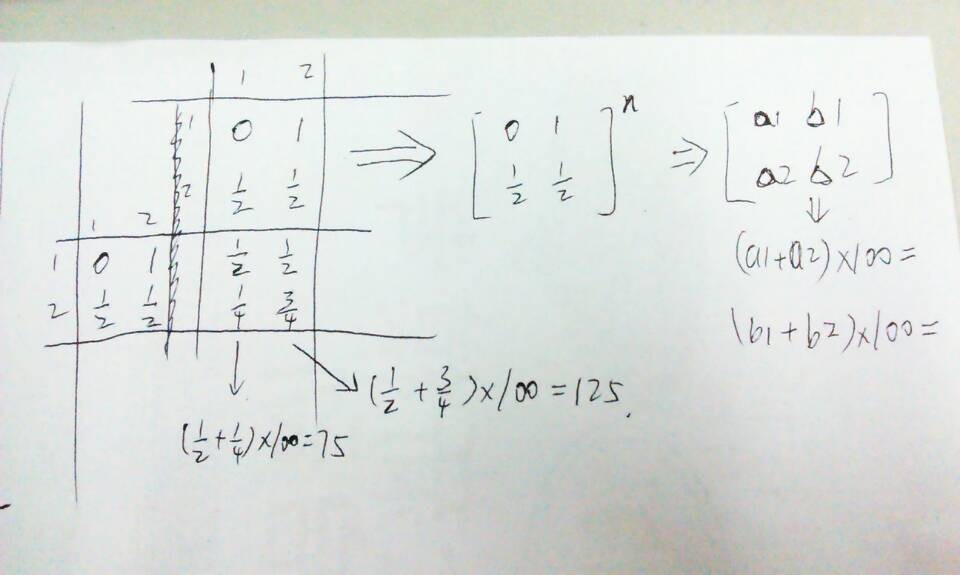
这道要变动提取一下矩阵，之后就简单了

具体解释可看代码：

#include <string.h>
#include <stdio.h>
#include<algorithm>
using namespace std;

int num;
struct matrix
{
       double a[][];//把每次倒水的比率提取出来放在这里面，例如i倒给j几分之几，以便进行计算
}origin,answ;//answ保存提取出来比率计算后的答案

matrix multiply(matrix x,matrix y)//x与y的矩阵乘法
{
       matrix temp;
       for(int i=;i<=num;i++)
       {
               for(int j=;j<=num;j++)
               {
                       double ans=;
                       for(int k=;k<=num;k++)
                       {
                               ans+=x.a[i][k]*y.a[k][j];
                       }
                       temp.a[i][j]=ans;
               }
       }

       return temp;
}

matrix calc(int n)//矩阵快速幂——把提取出来的比率进行n次重复的‘倒’，即n次幂
{
     while(n)//以下运用二分
     {
             if(n%==)
                    answ=multiply(origin,answ);
             origin=multiply(origin,origin);
             n/=;
     }
     return answ;
}

int main()
{
    int t,n,k,m;
    double a[];
    scanf("%d",&t);
    for(int id=;id<t;id++)
    {
        memset(answ.a,,sizeof(answ.a));
        memset(origin.a,,sizeof(origin.a));

        scanf("%d",&n);
        for(int i=;i<=n;i++)
            scanf("%lf",&a[i]);

        num=n;
        for(int i=;i<=n;i++)
            answ.a[i][i]=;

        for(int i=;i<=n;i++)
        {
            scanf("%d",&k);//i要平均的倒给之后的k个人
            if(k==)
                origin.a[i][i]=1.0;//不向任何地方倒，相当于都倒给自己，即1/1
            for(int j=;j<=k;j++)
            {
                int p;
                scanf("%d",&p);
                origin.a[p][i]=1.0/k;//i倒给p的比率
            }
        }

        scanf("%d",&m);
        calc(m);//对数据进行处理

        for(int i=;i<=n;i++)//逐个输出答案
        {
            double ans=;//初始化
            for(int j=;j<=n;j++)//一列一列处理
                ans+=answ.a[i][j]*a[j];//处理后的比率*原始数据
            if(i==)
                printf("%.2lf",ans);
            else
                printf(" %.2lf",ans);
        }
        puts("");
    }
    return ;
}