POJ1848--Tree ——树形dp

题意：给你一个树，问你最少连几条边可以让树中的每一个节点在且只在一个环内。如果无法完成就输出-1。

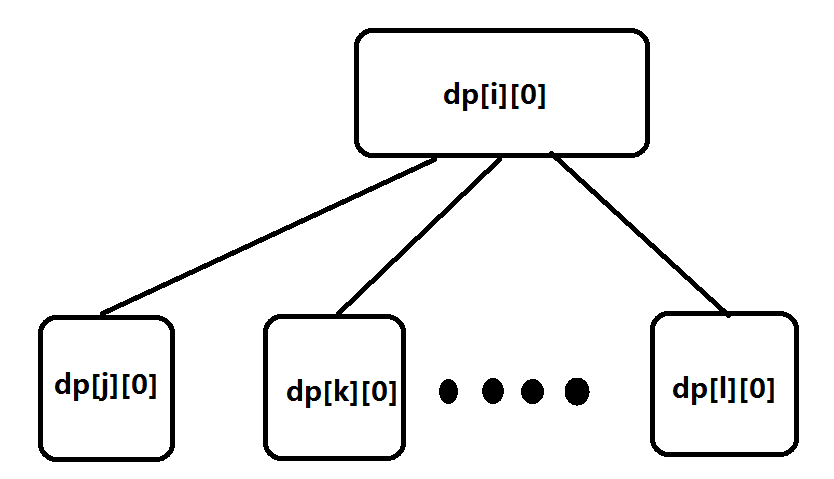
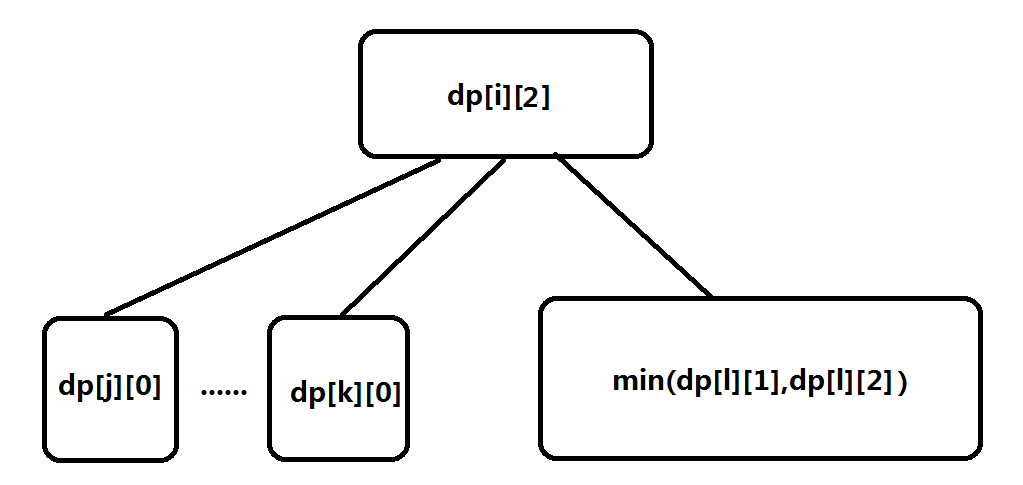
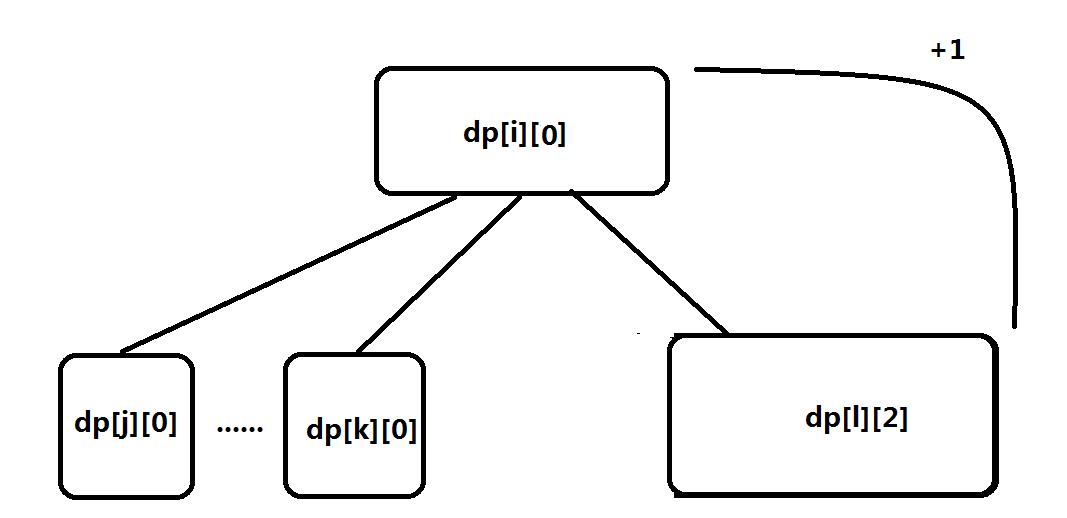
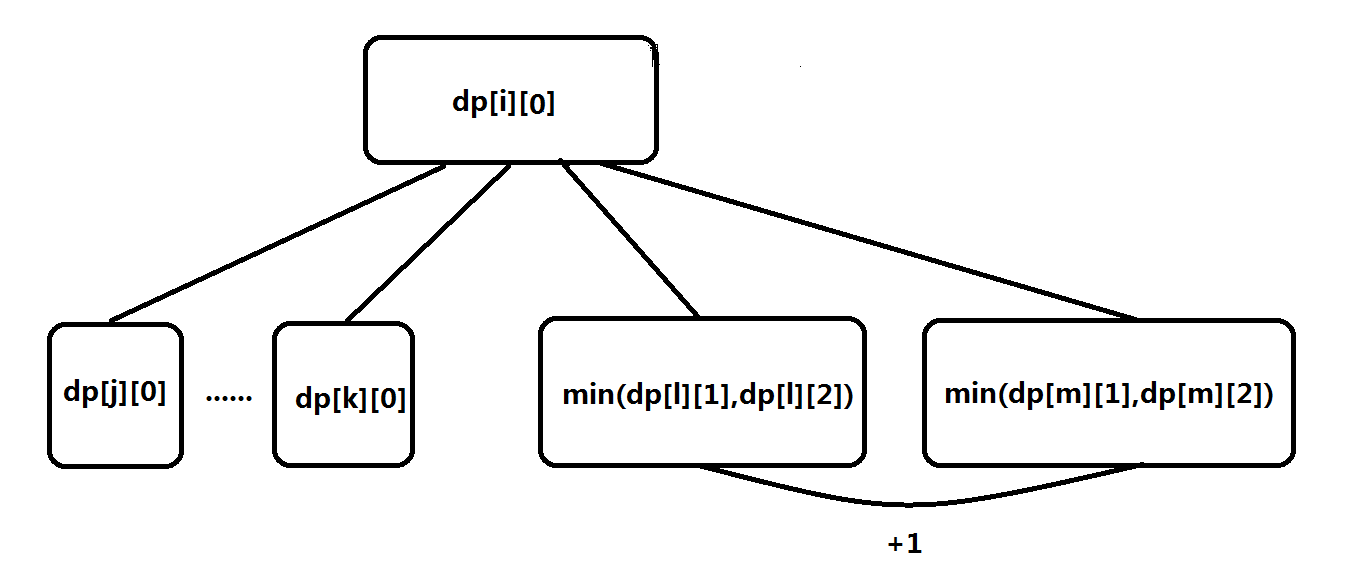
我们设dp[i][0]为根节点为i的树变成每一个节点都在且只在一个环里所需要的最小边数。dp[i][1]为除了根节点i外其他点都在且只在一个环里所需要的最小边数。

dp[i][2]为除了根节点和一个子节点（以及子节点可有可无的链）都在且只在一个环里所需要的最小边数。

这样我们的状态转移需要考虑以下4种情况：

（第一张图最上面应该是dp[i][1]  当时写错了不好改）

 

具体代码如下：

#include<iostream>
#include<vector>
using namespace std;
#define ll long long
const ll inf=;
ll dp[][];
vector<int> a[];
void solve(int u,int f)
{
    int i,j;
    if(a[u].size()==&&a[u][]==f)
    {
        dp[u][]=inf;
        dp[u][]=;
        dp[u][]=inf;
        //
        return;
    }
    for(i=;i<a[u].size();i++)
    {
        if(a[u][i]==f) continue;
        solve(a[u][i],u);
    }
    ll sum=;
    for(i=;i<a[u].size();i++)
    {
        if(a[u][i]==f) continue;
        sum+=dp[a[u][i]][];
    }
    dp[u][]=min(dp[u][],sum);
    for(i=;i<a[u].size();i++)
    {
        if(a[u][i]==f) continue;
        ll now=sum-dp[a[u][i]][]+min(dp[a[u][i]][],dp[a[u][i]][]);
        ll now1=sum-dp[a[u][i]][]+dp[a[u][i]][]+;
        dp[u][]=min(dp[u][],now);
        dp[u][]=min(dp[u][],now1);
    }
    for(i=;i<a[u].size()-;i++)
    for(j=i+;j<a[u].size();j++)
    {
        if(a[u][i]==f||a[u][j]==f) continue;
        ll now=+sum-dp[a[u][i]][]-dp[a[u][j]][]+min(dp[a[u][i]][],dp[a[u][i]][])+min(dp[a[u][j]][],dp[a[u][j]][]);
        //cout<<u<<i<<j<<" "<<min(dp[a[u][i]][1],dp[a[u][i]][2])<<" "<<min(dp[a[u][j]][1],dp[a[u][j]][2])<<endl;
        dp[u][]=min(dp[u][],now);
    }

}

int main()
{
    int i,n,x,j,y;
    cin>>n;
    for(i=;i<n-;i++)
    {
        cin>>x>>y;
        a[x].push_back(y);
        a[y].push_back(x);
    }
    for(i=;i<=n;i++)
    for(j=;j<=;j++) dp[i][j]=inf;
    solve(,-);
    ll ans=inf;
    ans=dp[][];
    if(ans==inf) cout<<"-1"<<endl;
    else cout<<ans<<endl;
    //for(i=1;i<=n;i++) cout<<dp[i][0]<<" "<<dp[i][1]<<" "<<dp[i][2]<<endl;
}