leetcode70 爬楼梯 Python

组合数学Fibonacci

例3.4.1   （上楼梯问题）某人欲登上n级楼梯，若每次只能跨一级或两级，问他从地面上到第n级楼梯，共有多少种不同的方法？

（解）设上到第n级楼梯的方法数为a_n。分类统计，那么，第一步有两种可能：

（1） 跨一级，则余下的n－1级有a_n－1种上法；

（2） 跨两级，则余下的n－2级有a_n－2种上法。

由加法原理 

F1	F2	F3	F4	F5	F6
1	1	2	3	5	8	……
	a1	a2	a3	a4	A5

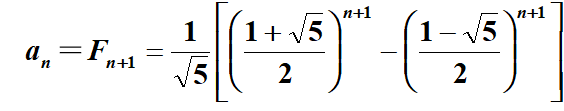
 import math

 class Solution(object):
     def climbStairs(self, n):
         """
         :type n: int
         :rtype: int
         """
         n = n+1
         if n <= 1:
             return 1
         if n == 2:
             return 2
         return int(1/math.sqrt(5) * (((1+math.sqrt(5))/2)**n-((1-math.sqrt(5))/2)**n))