3D数学基础（一）Unity坐标系

Unity引擎时非常成熟的，引擎内部运用了很多的数学知识，他对开发者来说是不可见的，而且他已经封装好的算法也不是很全面。此外，要是使用引擎封装好的算法也要明白其实现的原理。

写过一些代码，也参考了一些博客，书籍，想就此记录总结一下的自己所学到的东西，也给大家分享一下。

而我主要想从这五个方面来简要说说，分别是Unity坐标系，向量，矩阵，四元数，欧拉角。这篇先来介绍第一个。

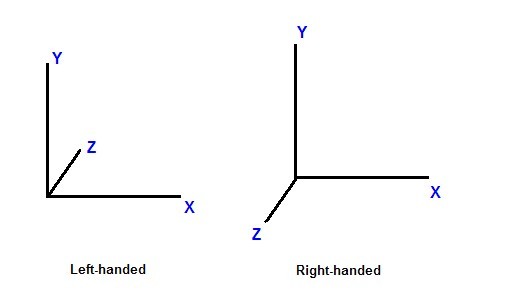
　　在介绍Unity的坐标系钱，我想先谈谈3D坐标系，表示的是三维空间，它存在着三个坐标轴，分别是X轴，Y轴，Z轴。3D坐标系分为左手坐标系和右手坐标系。左手坐标系就是Y轴指上方，X轴指向右方，而Z轴指向前方；而右手坐标系和左手坐标系的X轴和Y轴志向相同，Z轴的方向正好相反。便于理解：大拇指指向的方向就是Z轴的方向，四指弯曲的方向就是从X轴到Y轴的方向，左右手都可以这样判断。

　　（1）世界坐标（World Space）

　　Unity引擎的左手坐标系也被称为世界坐标系，在默认情况下，局部坐标和世界坐标系的原点是重合的，不能把所有的模型都叠加在世界坐标系的原点上，因此需要移动模型。模型移动式就会发生模型的局部坐标到世界坐标的转换，这个移动的过程就是把模型的局部坐标转化成世界坐标。知识这个转化的过程是在引擎编辑器内部实现的，实际上就是将模型的各个点与世界矩阵相乘得到。

　　X轴：左负右正；Y轴：上正下负；Z轴：里正外负。

　　transform.position就是获取到当前物体的世界坐标的位置。

　　transform.localPosition获取的是当前模型的局部坐标。

　　（2）屏幕坐标（Screen Space）

　　Unity开发的移动端手游经常会用到屏幕坐标系，屏幕坐标是就是通常使用的电脑屏幕，它是以像素为单位的，屏幕左下角（0，0）点，右上角为（Screen.Width,Screen.Height）点，Z的位置是根据相机的Z缓存值确定的。通常使用鼠标在屏幕上单机物体，它就是屏幕坐标。通过Input.mousePosition可以获得鼠标位置的坐标。对虚拟摇杆的滑动可以通过Input.GetTouch(0)，position获取到手指触碰屏幕的坐标。对UI的操作以及单机3D物体发射射线判断是否选中物体也是基于屏幕坐标系的。

　　（3）相机坐标（ViewPort Space）

　　通过相机才能看到虚拟世界的物体。相机有自己的适口坐标，物体要转换到视口坐标才能被看到。相机的视口左下角为（0，0）点，右上角为（1，1）点，Z的位置是以相机的世界单位来衡量的。（0，0）点和（1，1）点是通过公式进行缩放计算的。

　　（4）坐标转换

　　获取物体位置的通常写法是transform.position，它表示的时立方体在3D世界中的世界坐标的位置。如果使用的是触摸屏幕，那么可以通过函数Input.GetTouch(0).position获取到屏幕坐标系。

　　世界坐标和本地坐标可以直接从position和localPosition中获取；

　　世界坐标到屏幕坐标的转化:camera.WorldToScreenPoint(transform.position)；

　　世界坐标到视口坐标的转化:camera.WorldToViewportPoint(obj.transform.position);

　　屏幕坐标到视口坐标的转化:camera.ScreenToViewportPoint(Input.GetTouch(0).position)；

　　视口坐标到世界坐标的转化:camera.ViewportToWorldPoint(0.2f，0.3f，0);

　　视口坐标到屏幕坐标的转化:camera.ViewportToScreenPoint(0.2f，0.3f，0);