『Tarjan算法 有向图的强连通分量』

<更新提示>

<第一次更新>

---

<正文>

有向图的强连通分量

定义：在有向图\(G\)中，如果两个顶点\(v_i,v_j\)间\((v_i>v_j)\)有一条从\(v_i\)到\(v_j\)的有向路径，同时还有一条从\(v_j\)到\(v_i\)的有向路径，则称两个顶点强连通(\(strongly\ connected\))。如果有向图\(G\)的每两个顶点都强连通，称\(G\)是一个强连通图。有向图的极大强连通子图，称为强连通分量(\(strongly\ connected\ components\))。

万能的\(Tarjan\)算法也可以帮助我们求解有向图的强联通分量。

预备知识

时间戳

图在深度优先遍历的过程中，按照每一个节点第一次被访问到的顺序给\(N\)个节点\(1-N\)的标记，称为时间戳，记为\(dfn_x\)。

追溯值

设节点\(x\)可以通过搜索树以外的边回到祖先，那么它能回到祖先的最小时间戳称为节点\(x\)的追溯值，记为\(low_x\)。当\(x\)没有除搜索树以外的边时，\(low_x=x\)。

Tarjan 算法

著名的\(Tarjan\)算法可以在线性时间内求解有向图的强联通分量。

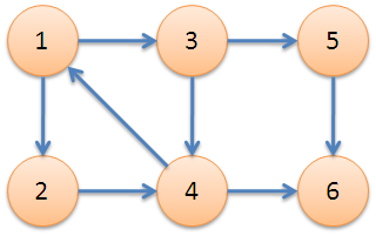
• 举个栗子，右图中，子图\(\{1,2,3,4\}\)为一个强连通分量，因为顶点\(1,2,3,4\)两两可达。\(\{5\},\{6\}\)也分别是两个强连通分量。

\(Tarjan\)求强连通分量的过程仍然是在递归求解\(dfn\)，\(low\)的过程中利用这两个数组实现的(如何求解可以参见(『Tarjan算法 无向图的割点与割边』)，其原理如下。

\(Tarjan\)算法将每个强连通分量看作图的搜索树中的一棵子树，搜索时，将每一个未回溯的节点加入一个栈，回溯时若\(dfn\)值与\(low\)值相等，则得到栈顶的当前节点以上的若干节点即为一个强连通分量。

我的理解：

回溯时若\(dfn\)值与\(low\)值相等，则说明以当前节点为根的子树中的若干节点都通过直接或间接路径返回到了当前节点，而当前节点到那些节点显然是可行的。也就是说，它们形成了若干个环，构成了一个强连通分量。

实际上，\(low\)数组就是不断在找"环"结构的过程。

其流程如下：

对于每一个当前访问的点：

1.更新\(dfn\)和\(low\)的初始标记，\(low=dfn\)

2.遍历当前节点的每一个子节点

3.如果其子节点未标记\(dfn\)值，访问并更新，并顺带更新\(low\)值

4.如果已经访问标记了\(dfn\)值，并且其子节点还在栈中，则该边是一条返祖边，更新\(low\)值

5.完成所有子节点的遍历后，判断\(dfn\)是否等于\(low\)，若相等，则说明当前栈顶的若干点(直到栈顶节点为当前节点)构成了一个强连通分量，记录即可

\(Code:\)

inline void Tarjan(int x)
{
	dfn[x]=low[x]=++cnt;
	Stack.push(x);inSta[x]=true;
	for(int i=Last[x];i;i=e[i].next)
	{
		int y=e[i].ver;
		if(!dfn[y])
		{
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(inSta[y])low[x]=min(low[x],dfn[y]);
	}
	if(dfn[x]==low[x])
	{
		int top=0;tot++;
		while(top!=x)
		{
			top=Stack.top();
			Stack.pop();
			inSta[top]=false;
			con[top]=tot;
			size[tot]++;
			//这些点都在编号为tot的一个强连通分量中，con为查询强连通分量的数组，size为强连通分量的大小
			//储存方式需要适时改变，以应合题目
		}
	}
}

Tarjan算法的应用

通常，我们可以通过\(tarjan\)算法找到有向图中的强连通分量，若将各个强连通分量压缩成一个点，我们就得到了一个有向无环图(\(DAG\))，这对我们的解题过程可以有所帮助。

最受欢迎的牛

Description

每头牛都有一个梦想：成为一个群体中最受欢迎的名牛！

在一个有N(1<=N<=10,000)头牛的牛群中，给你M(1<=M<=50,000)个二元组(A,B),表示A认为B是受欢迎的。

既然受欢迎是可传递的，那么如果A认为B受欢迎，B又认为C受欢迎,则A也会认为C是受欢迎的，哪怕这不是十分明确的规定。你的任务是计算被所有其它的牛都喜欢的牛的个数。

Input Format

第一行，两个数，N和M。

第2～M+1行，每行两个数，A和B，表示A认为B是受欢迎的。

Output Format

一个数，被其他所有奶牛认为受欢迎的奶牛头数。

Sample Input

3 3
1 2
2 1
2 3

Sample Output

1

解析

将牛的欢迎关系视为图的连边后，我们就得到了一张有向图，不过不能保证无环。

我们放宽限制，假设给出的是有向无环图，可以尝试几组样例。

发现规律后我们可以得到猜想：若有且仅有一个点出度为0，则该点符合要求，答案总数为1，若有多于一个点出度为0，则没有符合要求的点，答案总数为0。

那么对于原图，我们把每一个强连通分量压缩为一个点，按有向无环图的规律得到答案即可。若符合要求的点是一个由强连通分量压缩得到的点，则答案数量为该强连通分量的大小。

这就成了一道强连通分量缩点模板题。

\(Code:\)

#include<bits/stdc++.h>
using namespace std;
const int N=20000+200,M=80000+200;
int n,m,dfn[N],low[N],cnt,Last[M*2],t,con[N],tot,inSta[N],outdeg[N],size[N],ans=0;
stack < int > Stack;
struct edge{int ver,next;}e[M*2];
inline void insert(int x,int y)
{
	e[++t].ver=y;e[t].next=Last[x];Last[x]=t;
}
inline void input(void)
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=m;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		insert(x,y);
	}
}
inline void Tarjan(int x)
{
	dfn[x]=low[x]=++cnt;
	Stack.push(x);inSta[x]=true;
	for(int i=Last[x];i;i=e[i].next)
	{
		int y=e[i].ver;
		if(!dfn[y])
		{
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}
		else if(inSta[y])low[x]=min(low[x],dfn[y]);
	}
	if(dfn[x]==low[x])
	{
		int top=0;tot++;
		while(top!=x)
		{
			top=Stack.top();
			Stack.pop();
			inSta[top]=false;
			con[top]=tot;
			size[tot]++;
		}
	}
}
inline void build(void)
{
	for(int i=1;i<=n;i++)
		for(int j=Last[i];j;j=e[j].next)
			if(con[i]^con[e[j].ver])outdeg[con[i]]++;
}
inline void find(void)
{
	int flag=0;
	for(int i=1;i<=tot;i++)
		if(!outdeg[i])
		{
			if(!flag)flag=i;
			else
			{
				ans=0;
				return;
			}
		}
	ans=size[flag];
}
int main(void)
{
	input();
	for(int i=1;i<=n;i++)
		if(!dfn[i])Tarjan(i);
	build();
	find();
	printf("%d\n",ans);
	return 0;
}

---

<后记>