梯度提升决策树(GBDT）

1.提升树

　　以决策树为基函数的提升方法称为提升树。决策树可以分为分类树和回归树。提升树模型可以表示为决策树的加法模型。

　　针对不同的问题的提升术算法的主要区别就是损失函数的不同，对于回归问题我们选用平方损失函数，对于分类问题，我们使用指数损失函数。特别的，对于二分类问题，我们提升树就是把AdaBoost的基分类器选为二分类树即可。

　　对于回归问题的提升树，我们每一步都是在拟合残差，为什么是在拟合残差？，看公式

　　                                   

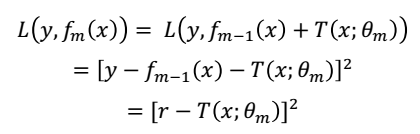
　　其中，r代表的就是残差。我们并不是说我们在拟合残差，而是说我们对于回归问题，选用平方损失函数，然后推导求解fm时，可以认为它是在拟合残差。

　　对应的回归问题的提升算法如下：

　　

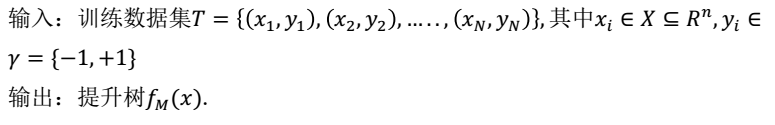
　　（1）初始化f0

　　（2）对m = 1,2,3...,M

　　　　(2.1) 计算每一个数据的残差：

　　　　　　　　　　　　　　　　　　　

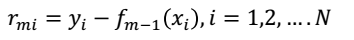
　　　（2.2）拟合残差学习一颗回归树，得到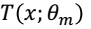

　　　（2.3）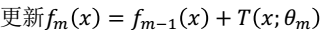

（3）得到回归问题的提升树

　　　　　　　　　　

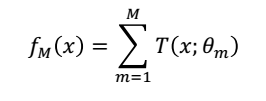
　　以上就是提升树的内容，主要理解为什么说提升树是拟合残差的，数学推导

2.梯度提升树

　　梯度提升的思想主要借鉴了梯度下降法。