多项式与三角函数求导——BUAA OO 第一单元作业总结

第一次作业

需求简要说明

针对符合规定的多项式表达式输出其符合格式规定的导函数多项式，格式错误输出WRONG FORMAT！

带符号整数 支持前导0的带符号整数，符号可省略，如： +02、-16>、19260817等。

幂函数
一般形式 由自变量x和指数组成，指数为一个带符号整数，如：x ^ +2。

省略形式 当指数为1的时候，可以采用省略形式，如：x。

项
变量项

带有系数的幂函数，如：2 * x ^ 2、-1 * x。

系数为1的时候，可以省略系数或表示为正号开头的形式，如：x ^ 2、+ >x ^ 2。

系数为-1的时候，可以表示为负号开头的形式，如：-x ^ 2。

常数项 包含一个带符号整数，如：233。

表达式 由加法和减法运算符连接若干项组成，如： -1 + x ^ 233 - x ^ >06。此外，在第一项之前，可以带一个正号或者负号，如：- -1 + x ^ 233>、+ -2 + x ^ 19260817。注意，空串不属于合法的表达式。

空白字符 在本次作业中，空白字符包含且仅包含<space>和\t。

此外，值得注意的几点是：

带符号整数内不允许包含空白字符。

幂函数、项、表达式，在不与上一条矛盾的前提下，可以在任意位置包含任意数量的>空白字符。

如果某表达式存在不同的解释方式，则只要有任意一条解释中是合法的，该表达式即>为合法。

题目分析与程序设计

第一次作业比较简单，只包含变量项和常数项，而且求导方式单一。为了最大程度的简化逻辑，我使用指数为0表示常数项，这样每个项的表示方式就统一起来了。因此，层次划分到项为止，并没有继续区分系数、因子等内容。为了更好地管理格式的统一处理，我建立了FormChecker类统一检查并初步处理字符串格式（包括空格删除、多个运算符合并等），并完成字符串的切割与格式检查。所有操作都使用正则表达式完成。

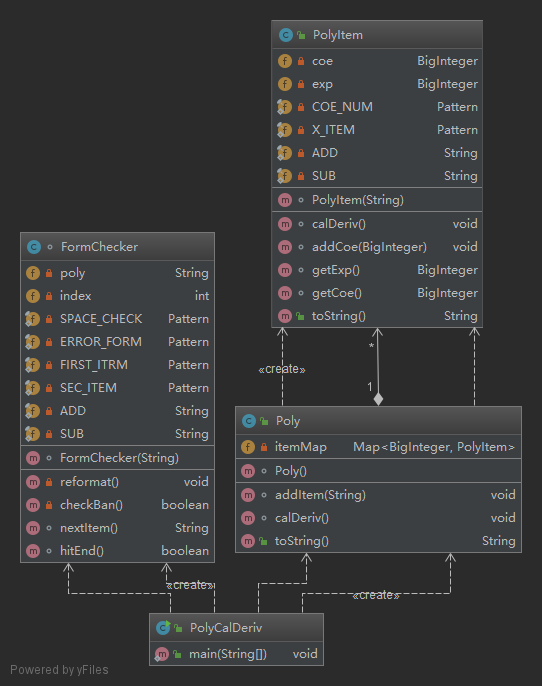
数据结构方面我直接使用了HashMap作为主要的索引结构，使用项的指数作为作为Key，PolyItem作为value就可以很方便的构建并发现、合并同类项。

代码分析

第一次作业在中测和强测中都没有出现bug，但因为我忽视了优化部分，因此被扣除了一些性能分。第一次作业代码的度量分析如下：

项目	平均值	特殊值
Line Of Codes (总行数)	类平均：71.5，方法平均：12.9	PolyItem类：100，PolyItem类的toString方法：36
Cyclomatic Complexity（循环复杂性）	3	PolyItem类的toString方法：9
Parameter Count（参数计数）	0.3125
WMC (类平均加权方法复杂度)	12	PolyItem类：20
Depth of Inheritance Tree（继承树深度）	0
Operation Complexity Average（平均操作复杂度）	3	PolyCalDeriv：5
平均注释量	2%

这是我第一次写面向对象程序，从代码分析中也可以看出，除了根据功能划分了不同的类别，切分了方法之外，没有任何面向对象的特点，类之间除了create关系之外基本是独立的，没有内在的层次或者其他联系。代码中虽然做了功能切分，但还是不可避免的将大部分的计算以及结构化的任务留给了PolyItem类，使得这个类不仅出现了超长的方法，整个类也变得比较复杂。在这次作业的完成过程中，我没有很熟练的使用checkstyle代码规范工具，导致浪费了好几次提交机会都是为了规范代码；而且也没有很注意及时给出代码注释，代码的注释量很低。综合来看，这次作业虽然完成了功能，但是代码的可读性较差，维护起来也比较困难。

第二次作业

需求简要说明

第二次作业基本上是在第一次作业的基础上进行的，增加了三角函数的处理，以及一些额外的格式规定。

三角函数 sin(x)或cos(x)（在本次作业中，括号内仅为x）

一般形式 类似于幂函数，由sin(x)和指数组成，指数为一个带符号整数，如：sin(x) ^ +2。

省略形式 当指数为1的时候，可以采用省略形式，省略指数部分，如：sin(x)。

常数因子 包含一个带符号整数，如：233。

项
一般形式 由乘法运算符连接若干因子组成，如：2 * x ^ 2 * 3 * x ^ -2、sin(x) * cos(x) * x。

此外，值得注意的几点是：

三角函数的保留字内不允许包含空白字符，即sin和cos内不可以含有空白字符。

未知数包含且仅包含小写的x。

题目分析与程序设计

第二次作业相比较第一次作业复杂度有所上升，主要在于将因子的概念拓展了，这意味这我不能再像第一次那样采用统一的格式规定因此，因此我单独实现了一个PolyFactor类并借助枚举来识别类实体对应的不同因子类型。而对于每类因此，他们的相同之处还是很明显的，也就是他们都有且只有一个数字作为参数——对于非常数因子就是指数，常数因子就是值本身。

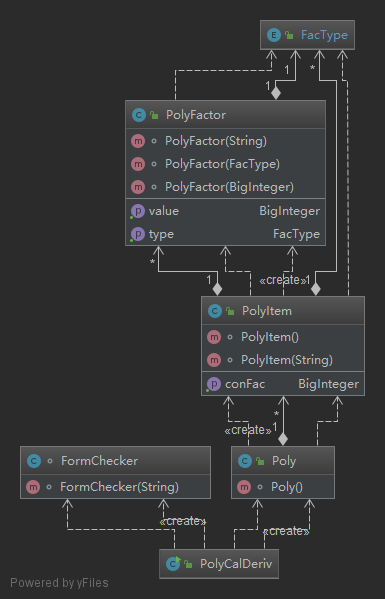
而对于表达式的输出优化部分，我除了常规的同类项同类因子合并之外，完成了形如sin^2和cos^2之间的合并，并没完成更高次项的合并。数据结构方面，为了依旧使用HashMap作为主要的数据结构，我在PolyItem使用了FacType->PolyFactor的map；在Poly中的实现时重写了PolyItem的hashCode和equals函数，从而得以使用PolyItem->PolyItem的map。这样的数据结构管理方式使得我的多项式在任何时候都不会出现同类项或者同类因子并存的情况，可以说简化了后面的计算过程。

代码分析

第二次作业我在中测和强测中均无bug，但是强测时由于没有进行单间函数拆分合并，依旧是被扣掉了不少性能分。这次作业的代码分析如下：

项目	平均值	特殊值
Line Of Codes （总行数）	类平均：114.8，方法平均：13.63	PolyItem类：197，PolyItem类的toString方法：34
Cyclomatic Complexity（循环复杂性）	3.05	PolyItem类的toString方法：9
Parameter Count（参数计数）	0.389
WMC（类平均加权方法复杂度）	22	PolyItem类：39
Depth of Inheritance Tree（继承树深度）	0
Operation Complexity Average（平均操作复杂度）	3.11	PolyCalDeriv：5
平均注释量	14%

这次作业我对然单独划分了PolyFactor类，但是选择了功能整合而非功能切割，这使得我的PolyFactor类不管是建立还是操作都有很高的复杂性。而且相应的，对于PolyItem类也造成了不小的负担，而且我的优化操作主要集中在了PolyItem类中，这使得这个类功能比较臃肿。关于这一点，在我后期debug的时候劣势体现的比较明显。首先是每个方法的职责划分不够详细，因此为了保证正确性我只能一遍又一遍的判断，无疑增加了代码的复杂程度；其次，我虽然有意识的使用了同名函数规范相同的功能，但是这一点做得不够完全，突出提现在PolyFactor和PolyItem两个类中，我都实现了combine函数，但实际上两个函数的输入前提并不很一直，返回值的情况也不完全相同，导致这部分经常出现各种莫名的bug。

第三次作业

简要需求说明

在第二次作业的基础上加入了因子嵌套，其余规则保持不变。

表达式因子 将在表达式的相关设定中进行详细介绍。不过，表达式因子不支持幂运算。

嵌套因子 本次作业将支持因子嵌套在三角函数因子里面，即一个因子作为另一个三角函数因子的自变量，例如sin(x^2)，cos(sin(x))以及sin(sin(cos(cos(x^2))))^2等。但是不允许出现指数为变量的情况，指数依然只能是带符号整数，例如sin(x) ^ sin(x)是不合法的，因为指数不是自变量。也不允许幂函数的自变量为除了x之外的因子，例如1926^0817是不合法的，因为幂函数的自变量只能为x。

项
一般形式 由乘法运算符连接若干任意因子组成，如：x * cos(x) * x，sin(x ^ 2) * cos(sin(x)) ^ 2 * x ^ -2等。

项内因子不仅仅是同类因子

表达式 由加法和减法运算符等若干项组成，如： (-1 + x ^ 233)* sin(x^2) ^ 06 - cos(sin(x)) * 3 * sin((x))。此外，在第一项之前，可以带一个正号或者负> 号，如：- -1 + x ^ 233、+ -2 + x ^ 1926。此处有几点注意：
表达式因子，表达式可以作为因子，其定义为被一对小括号包裹起来的表达式，即我们允许诸如(x * cos(x)) 这种式子的出现

空串不属于合法的表达式

空白字符 在本次作业中，空白字符包含且仅包含<space>和\t。其他的除了上述会用到的字符之外，均属于非法字符。

此外，值得注意的几点是：

表达式因子可以递归嵌套，例如sin( ( x^2 + sin((1 + 3*x)) ) )

为了方便评测机评测，我们限制的指数的绝对值不超过$10^4$，超过此范围需要输出 WRONG FORMAT!

（重大更新） 对于类似sin((x-x))^-1的输入，会存在除0的情况，对于评测是非常难处理的，故对指导书进行补充。为了保证向下兼容，我们限制所有的指数必须严格大于0，这一条作为基本限制，任何测试数据不得违背该限制，不需要对此输出WRONG FORMAT!。此外，我们将0^0一概定义为1（即c标准库和python中的定义）

题目分析与程序设计

由于本次作业需求中加入了对因子的嵌套处理以及表达式作为因子的情况，使用正则表达式处理字符串显得不是很有效，因此我这次使用切割的办法将整个字符串根据括号匹配切分为项和因子，再根据不同类的构造函数建立数据结构。为了能够统一类接口，我将Poly类的构造方式和Item、Factor统一起来，在Poly内部实现字符串切分，将Formchecker的功能简化到只剩下字符串的预处理，这样做的好处就是构建Expe因子类的时候之间调用Poly的构造函数即可。

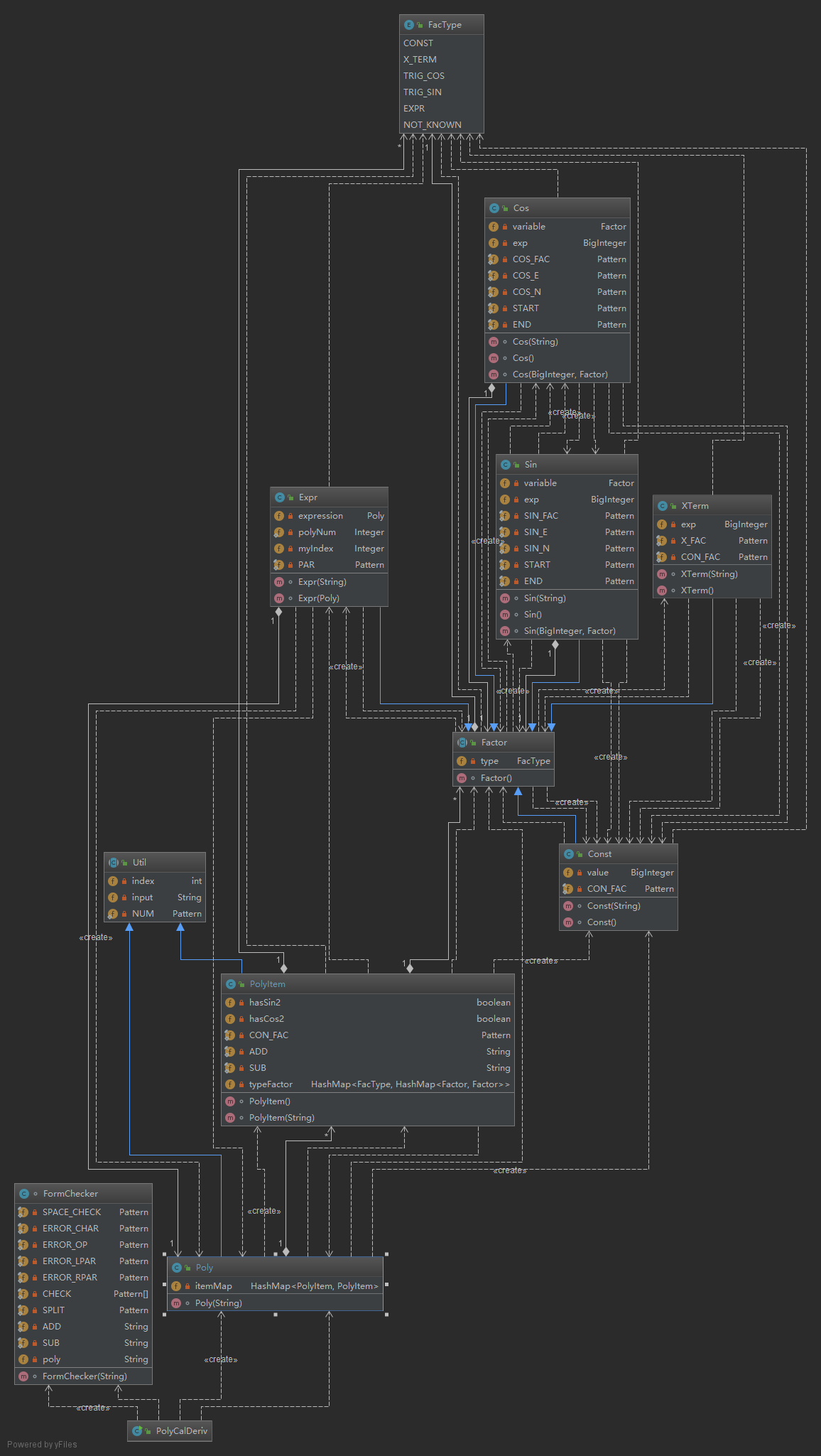
从类图中可以看出，这次代码的层次结构明显复杂了，因为我分别实现了各个因子类，但是又需要统一调用，因此他们必须有统一的父类或者实现同一个接口。实现过程中我发现接口的设计虽然有default标志，但是无法再override下使用default，这样的特点无疑会降低我代码的重用性。因此我选择使用抽象类作为他们的统一父类，将共性方法写成具体方法，实现无法统一的方法作为抽象方法，这样构建起来整个Factor的组织结构。除此之外，我还意识到Poly类和PolyItem也是具有类似特点的，例如他们都需要切分处理字符串，都需要对下层hashString进行有序插入，都需要求导和化简。所以我在这里也构建了Util抽象类组作为他们的父类，进一步简化了代码结构，使得整体的组织方式更加清晰。
数据结构方面，我依旧保持了原来的hashMap设计，通过hashString->hashCode的转化不仅能够建立map而且可以方便的判断同类项和同类因子。

吸取第二次作业的教训，这次作业我在一开始就规范了一些通用函数（如：combine、add等）的功能与表现，借助抽象函数更好地规范了他们的接口，使得职责划分较为明确，这在我后期debug的时候方便了不少。

代码分析

这次作业我并没有花时间做太多优化，只是完成了简单地去括号等优化处理。中测没有bug，强测的时候出现了一个bug，原因是我在处理字符串采用了切分的方式，而样例中最后多了一个*，这使得我切分后无法得到该因子，产生了索引越界的错误。
这个问题的出现我认为主要是我对错误处理机制还是建立的不够完善，我没有使用exception结构，如果使用了这样的结构在这种有可能出现问题的地方catch一下也就可以避免程序crash了。
这次作业的代码分析如下：

项目	平均值	特殊值
Line Of Codes （总行数）	类平均：92.82，方法平均：9.32	PolyItem类：240，Util类的nextItem方法：49
Cyclomatic Complexity（循环复杂性）	2.26	Factor类的typeDet方法：20
Parameter Count（参数计数）	0.46
WMC（类平均加权方法复杂度）	19.18	PolyItem类：49
Depth of Inheritance Tree（继承树深度）	0
Operation Complexity Average（平均操作复杂度）	2.24	PolyCalDeriv：3.5
平均注释量	14%

这次作业我主要关注了facotr的功能实现，对于降低PolyItem的复杂性而言并没有太多更改，因此相较第二次作业PolyItem的复杂度依然很高，而令我惊讶的是Factor类中的typeDet方法循环复杂性居然很高，实际上我并没有在这个函数中使用循环，只是使用了一个switch语句进行分支处理而已，我需要再详细了解一下循环复杂性的计算机制。
通过这次作业，我第一次真正体会到了面向对象的强大整合能力，以及类提供的多态特点的易用性。继承关系使得代码中层次划分非常明确，而接口的实现使得有不同行为不同对象可以被统一的组织与处理。这些特点都给实现和维护带来了很大的便利。