2018年山东省省队集训 Round 1 Day 2简要题解

从这里开始

• Problem A 生日礼物
• Problem B 咕咕
• Problem C 解决npc

　　（相信来看这篇博客的人都有题面）

　　T2以为可以线性递推，然后花了两个小时。然后想了两个小时T1，会了一个能过的算法。但是没时间写，sad.....比赛快结束时，发现T2模数$10^9+7$，内心mmp。

Problem A 生日礼物

题目大意

　　给定一个$n\times m$的网格图，每个格子中有一个不是0就是1的数，要求对于任意$w\times h$的子矩阵的和都相等，问方案数。

　　（为了简洁，各式子的范围请自行脑补）

　　瞎推推不难发现对于一个格子$(x, y)$，满足$a_{x, y} + a_{x + w, y + h} = a_{x + w, y} + a_{x, y + h}$。

　　移项得：

$\begin{align}a_{x, y} - a_{x + w, y} = a_{x, y + h} - a_{x + w, y + h}\end{align}$

　　用归纳法能够得出对于每连续的$w + 1$行，对模$h$的剩余相同的列，这$w + 1$行中的第一行和最后一行的上的数之差相等。

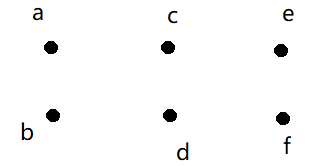
　　对于上图来说就是$a - b = c - d = e - f$。

　　考虑先确定前$w$行，每次在后面添加一行。显然这一行我们只用考虑前$h$个数（剩下的用式$(1)$来确定）。

　　考虑每一处$(i, j)$和它上面第$w$个格子上的数的差$d$

• 若$d = 1$，则说明$a_{i - w, j + kh} = 0 (k = 0, 1, \dots)$
• 若$d = 0$，则什么都不能说明
• 若$d = -1$，则说明$a_{i - w, j + kh} = 1 (k = 0, 1, \dots)$

　　所以变化量能为$1,-1$的只有当这一行上纵坐标模$h$同余于它的位置上的数等于它。

　　然后发现只要确定左上角的$w\times h$的矩形的状况，剩下的就能用快速幂计算。

　　然后我的做法就比较沙雕了。

　　$f_{s}$表示恰好包含$s$中的位置作为横着相同的格子，且将前$w$行填满的方案数。（不考虑这些格子上的数）

　　这个首先需要考虑这些格子上的数，进行容斥和子集和变换，再将这些格子上的数的贡献减去。

　　然后单独考虑这个矩阵中每一行的贡献，枚举$0$和$1$的数量，就可以计算贡献了。

Code

 #include <iostream>
 #include <cassert>
 #include <cstdlib>
 #include <cstdio>
 using namespace std;
 typedef bool boolean;

 const int Mod = 1e9 + ;

 int add(int a, int b) {
     return ((a += b) >= Mod) ? (a - Mod) : (a);
 }

 int sub(int a, int b) {
     return ((a -= b) < ) ? (a + Mod) : (a);
 }

 int mul(int a, int b) {
     return a * 1ll * b % Mod;
 }

 int qpow(int a, int p) {
     int rt = , pa = a;
     for ( ; p; p >>= , pa = mul(pa, pa))
         if (p & )
             rt = mul(rt, pa);
     return rt;
 }

 const int S =  << ;

 int n, m, w, h;
 int f[S], bit[S];
 int c[][], sc[][];
 int d[][], sd[][];
 int comb[][] = {{, , , , }, {, , , , }, {, , , , }, {, , , , }, {, , , , }};
 int invs[];

 inline void init() {
     scanf("%d%d%d%d", &n, &m, &w, &h);
 }

 int getline(int s, int l) {
     int rt = (s >> l) & ;
     for (int i = ; i < w; i++)
         rt = (((s >> (h * i + l)) & ) << i) | rt;
     return rt;
 }

 int getrow(int s, int row) {
     int msk = ( << h) - ;
     return s >> (h * row) & msk;
 }

 inline void solve() {
     d[][] = ;
     for (int i = ; i < ; i++)
         for (int j = ; j <= i; j++) {
             d[i + ][j] = add(d[i + ][j], d[i][j]);
             d[i + ][j + ] = add(d[i + ][j + ], d[i][j]);
         }

     int sl_repeat = m / h;
     for (int i = ; i <= ; i++)
         for (int j = ; j <= i; j++)
             sd[i][j] = qpow(d[i][j], sl_repeat);

     bit[] = ;
     for (int i = ; i < S; i++)
         bit[i] = bit[i >> ] + (i & );

     int all =  << (w * h);
     for (int s = ; s < all; s++) {
         f[s] = ( << bit[s]);
         for (int l = ; l < h; l++) {
             int sl = getline(s, l);
             int blank = w - bit[sl];
             int cmp = ;
             boolean aflag = ((m % h) > l);
             for (int i = ; i <= blank; i++)
                 cmp = add(mul(sd[blank][i], (aflag) ? (d[blank][i]) : ()), cmp);
             f[s] = mul(f[s], cmp);
         }
     }

     int size = w * h;
     for (int i = ; i < size; i++)
         for (int j = ; j < all; j++)
             if (!((j >> i) & ))
                 f[j] = sub(f[j], f[j ^ ( << i)]);

     for (int k = ; k <= ; k++)
         for (int c0 = ; c0 <= k; c0++) {
             int c1 = k - c0, ava = min(c0, c1);
             int& res = c[c0][c1];
             for (int use = ; use <= ava; use++) {
 //                res = add(res, mul(comb[c0][use], mul(comb[c1][use], fac[use])));
                 res = add(res, mul(comb[c0][use], comb[c1][use]));
             }
             sc[c0][c1] = qpow(res, n / w - );
         }

     invs[] = ;
     for (int i = ; i <= ; i++)
         invs[i] = qpow( << i, Mod - );
     for (int i = ; i < all; i++)
         f[i] = mul(f[i], invs[bit[i]]);

     int res = ;
     for (int s = ; s < all; s++) {
         if (!f[s])
             continue;
         int tmp = ;
         for (int r = ; r < w; r++) {
             int sr = getrow(s, r);
             int spe = bit[sr], cmp = ;
             boolean aflag = ((n % w) > r);
             for (int c0 = ; c0 <= spe; c0++) {
                 cmp = add(cmp, mul(mul(::sc[c0][spe - c0], ((aflag) ? (c[c0][spe - c0]) : ())), comb[spe][c0]));
             }
             tmp = mul(tmp, cmp);
 //            cerr << sr << " " << s << " " << r << " " << cmp << '\n';
         }
 //        if (tmp && f[s])
 //            cerr << s << " " << mul(f[s], tmp) << '\n';
         res = add(res, mul(f[s], tmp));
     }
     printf("%d\n", res);
 }

 int main() {
     init();
     solve();
     return ;
 }

Problem A

Problem B 咕咕

题目大意

　　有$n$种物品，每种物品无限个，第$i$种物品的体积为$a_i$。设$f(n)$表示恰好填满容量为$n$的背包的方案数，求$\sum_{i = L}^{R}f(i)$。

　　（这道题的名称告诉了我们不想掉rating的正确做法）

　　（我们可以线性递推 + 三模数NTT）

　　考虑每加入一个物品相当于对模$a_i$同余于$j\ (j = 0, 1, \dots, a_i - 1)$的地方分别做一次前缀和。

　　所以对于模$[a_{1}, a_{2}, \cdots, a_{n}]$余$r$的地方可以用一个$n - 1$次多项式表示。

　　由于要求前缀和，就再加入体积为$1$的物品。

　　对于$L-1,R$处的取值直接用$Lagrange$插值。

Code

 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 using namespace std;
 typedef bool boolean;

 #define ll long long

 const int N = , S =  * N;
 const int Mod = 1e9 + ;

 int add(int a, int b) {
     return ((a += b) >= Mod) ? (a - Mod) : (a);
 }

 int sub(int a, int b) {
     return ((a -= b) < ) ? (a + Mod) : (a);
 }    

 int mul(int a, int b) {
     return a * 1ll * b % Mod;;
 }

 void exgcd(int a, int b, int& x, int& y) {
     if (!b)
         x = , y = ;
     else {
         exgcd(b, a % b, y, x);
         y -= (a / b) * x;
     }
 }

 int inv(int a, int n) {
     int x, y;
     exgcd(a, n, x, y);
     return (x < ) ? (x + n) : (x);
 }

 int n, prod = , m;
 int a[N], f[S];

 inline void init() {
     scanf("%d", &n);
     for (int i = ; i < n; i++)
         scanf("%d", a + i), prod *= a[i];
     m = prod * (n + );
     f[] = ;
     for (int j = ; j < n; j++)
         for (int i = ; i <= m; i++)
             if (a[j] <= i)
                 f[i] = add(f[i - a[j]], f[i]);
     for (int i = ; i <= m; i++)
         f[i] = add(f[i], f[i - ]);
 }

 int Lagrange(ll _x) {
     if (_x <= m)
         return f[_x];
     int k = _x % prod;
     int x = (_x / prod) % Mod;
     int rt = ;
     for (int i = ; i <= n; i++) {
         int tmp = f[i * prod + k];
         for (int j = ; j <= n; j++)
             if (i ^ j)
                 tmp = mul(tmp, mul(sub(x, j), inv(sub(i, j), Mod)));
         rt = add(rt, tmp);
     }
     return rt;
 }

 ll l, r;
 inline void solve() {
     scanf("%lld%lld", &l, &r);
     printf("%d\n", sub(Lagrange(r), Lagrange(l - )));
 }

 int main() {
     init();
     solve();
     return ;
 }

Problem B

Problem C 解决npc

题目大意

　　要求构造一个点数不超过$50$，边数不超过$100$的有向图，使得它的本质不同的拓扑序的个数为$x$。

　　当$x = 1,2$的时候特判。

　　当$x$不大的时候，构造一条链和一个点就行了。

　　当$x$比较大的时候，考虑这样一个东西：

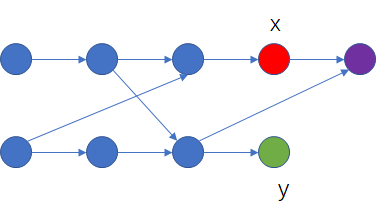
　　考虑在加入紫色节点前，以红色节点结尾的拓扑序的个数为$x$，以绿色节点结尾的拓扑序的个数为$y$，如图所示加入紫色节点，那么不难得到以紫色节点为结尾的拓扑序有$x + y$个。

　　那么就可以直接爆搜了。

Code

 #include <iostream>
 #include <cstdlib>
 #include <cstdio>
 #include <vector>
 using namespace std;
 typedef bool boolean;

 #define pii pair<int, int>

 const int Lim = ;

 int X;

 inline void init() {
     scanf("%d", &X);
 }

 int type[Lim + ];
 vector<pii> E;
 void dfs(int x, int y, int d, int lim) {
     if (d == lim || d == Lim || x + y > X)
         return;
     if (x + y == X) {
         vector<int> L(), R();
         L[] = , L[] = , R[] = , R[] = ;
         E.push_back(pii(, ));
         E.push_back(pii(, ));
         E.push_back(pii(, ));
         for (int i = ; i < d; i++)
             if (!type[i]) {
                 E.push_back(pii(L.back(), i));
                 E.push_back(pii(R[R.size() - ], i));
                 L.push_back(i);
             } else {
                 E.push_back(pii(R.back(), i));
                 E.push_back(pii(L[L.size() - ], i));
                 R.push_back(i);
             }

         printf("%d %d\n", d, (signed) E.size());
         for (int i = ; i < (signed) E.size(); i++)
             printf("%d %d\n", E[i].first, E[i].second);
         exit();
     }

     type[d] = ;
     dfs(x + y, y, d + , lim);
     type[d] = ;
     dfs(x, x + y, d + , lim);
 }

 inline void solve() {
     if (X == ) {
         printf("2 1\n0 1\n");
     } else if (X == ) {
         printf("3 2\n0 1\n2 1\n");
     }else if (X <= ) {
         printf("%d %d\n", X, X - );
         for (int i = ; i < X - ; i++)
             printf("%d %d\n", i, i + );
     } else {
         for (int lim = ; lim <= ; lim++)
             dfs(, , , lim);
         puts("Failed");
     }
 }

 int main() {
     init();
     solve();
     return ;
 }

Problem C