数论专场 Day9 部分题解

// 2019年西电暑期集训

// [7月9日]基础数论：https://cn.vjudge.net/contest/309097

A - Visible Lattice Points

题目大意：

平面上有N*N个格点，问从原点（0，0）能够看到多少个不被遮挡的点。

数据范围：1<=N<=1000，测试组数：1<=C<=1000。

分析及代码：

暴力计算复杂度N*N*C，肯定T。看题目所给几组样例，也没有发现有什么规律。

注意到点的分布的对称性，对于每一列（x=xi)，记录在直线y=x以下能看到的点的坐标：

（1，1）

（2，1）

（3，1），（3，2）

（4，1），（4，3）

（5，1），（5，2），（5，3），（5，4）

......

可以发现直线x=xi上的点的个数为与xi互质的个数，即欧拉函数值phi(xi)。

由对称性，（1，1）重复计算，加上点（1，0）与（0，1），所以本题答案为2*∑phi(xi) + 1。

#include <iostream>
#include <cstdio>
using namespace std;

const int maxn  = ;
int phi[maxn+];

void phi_table(int n) { // O(nlogn) n以内欧拉表
    int i, j;
    for(i=;i<=n;i++)
        phi[i] = i;

    for(i=;i<=n;i+=)
        phi[i] /= ;

    for(i=;i<=n;i+=) {
        if(phi[i]==i) {
            for(j=i;j<=n;j+=i)
                phi[j] = phi[j] / i * (i - );
        }
    }

    for(int i=;i<=n;i++) {  // 前缀和
        phi[i] += phi[i-];
    }
}

int main()
{
    phi_table();
    int T, t = , n;
    cin>>T;
    while(t++<T) {
        scanf("%d", &n);
        printf("%d %d %d\n", t, n, phi[n]*+);
    }
    return ;
}

B - Super A^B mod C

题目大意：

计算A^B (mod C)的结果，其中1<=A,C<=1000000000,1<=B<=10^1000000。

分析及代码：

B的数位长度达到了1000000位，即使利用快速幂logn的算法也有些勉强。。。

依稀记得有一个欧拉定理（费马小定理），计算当m为素数时a^b % m结果为a^(b%(m-1))，指数立刻收缩到了ll范围内。

这里需要用到a和m不互质情况下的欧拉降幂公式：

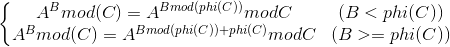
至于为什么我AC的代码指数没有加上phi(C)也过了，我也不懂O.O

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int maxn = ;
typedef long long ll;
ll a, c;
char b[maxn];

ll phi(ll x) {  // 欧拉函数
    ll res = x;
    for(int i=;i<=x/i;i++) {
        if(x%i==) {
            res = res/i*(i-);
            while(x%i==) x/=i;
        }
    }
    if(x>) res = res/x*(x-);
    return res;
}

ll pow(ll a, ll n) { // 快速幂
    ll res = ;
    while(n) {
        if(n&) res = res * a % c;
        a = a*a % c;
        n >>= ;
    }
    return res;
}

int main() {
    while(scanf("%lld", &a)!=EOF) {
        scanf("%s", b);
        scanf("%d", &c);
        ll exp = , p = phi(c);
        for(int i=;b[i];i++) {
            exp *= ;
            exp += b[i]-'';
            exp %= p;
        }
        // exp += p;
        printf("%lld\n", pow(a, exp));
    }
    return ;
}

D - The Euler function

题目大意：

求一段区间的欧拉函数值的和。（2<a<b<3000000）

分析及代码：

欧拉函数裸题，使用O(nlogn)欧拉筛预处理。

（预先求前缀和的算法比直接区间求和要慢。。。）

#include <iostream>
#include <cstdio>
using namespace std;

const int maxn  = ;
typedef long long ll;
ll phi[maxn];

void phi_table(int n)
{
    int i, j;
    for(i=;i<=n;i++)
        phi[i] = i;

    for(i=;i<=n;i+=)
        phi[i] /= ;

    for(i=;i<=n;i+=) {
        if(phi[i]==i) {
            for(j=i;j<=n;j+=i)
                phi[j] = phi[j] / i * (i - );
        }
    }

    for(int i=;i<=n;i++) {
        phi[i] += phi[i-];
    }
}

int main()
{
    phi_table();
    int a, b;
    while(scanf("%d %d", &a, &b)!=EOF) { // 此题直接写for循环更快
        printf("%lld\n", phi[b]-phi[a-]);
    }
    return ;
}

E - Strange Way to Express Integers

题目大意：

中国剩余定理裸题。。。

分析及代码：

还不是特别熟悉，网上找了份mi不互质的模板，稍微改改就直接A了。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
const int maxn = ;
ll exgcd(ll a, ll b, ll& x, ll& y) {
    ll d = a;
    if(b!=) {
        d = exgcd(b, a%b, y, x);
        y -= (a/b) * x;
    } else {
        x = ; y = ;
    }
    return d;
}

ll a[maxn], m[maxn], n;
ll CRT() {
    if (n == ) {
        if (m[] > a[]) return a[];
        else return -;
    }
    ll x, y, d;
    for (int i = ; i < n; i++) {
        if (m[i] <= a[i]) return -;
        d = exgcd(m[], m[i], x, y);
        if ((a[i] - a[]) % d != ) return -;   //不能整除则无解
        ll t = m[i] / d;
        x = ((a[i] - a[]) / d * x % t + t) % t; //第0个与第i个模线性方程的特解
        a[] = x * m[] + a[];
        m[] = m[] * m[i] / d;
        a[] = (a[] % m[] + m[]) % m[];
    }
    return a[];
}

int main() {
    while(scanf("%lld", &n)!=EOF) {
        for(int i=;i<n;i++) {
            scanf("%lld %lld", &m[i], &a[i]);
        }
        printf("%lld\n", CRT());
    }
    return ;
}

F - C Looooops

题目大意：

求A + Cx = B (mod 2^k) 的x最小正整数解。

分析及代码：

上式变形得到

C*x + 2^k*y = B-A

利用扩展欧几里得ax+by=gcd(a,b)解该同余方程，得到x。

• 若 (B-A) % gcd(a, b) 不为0，则无解。
• 否则 x = x * (B-A) / gcd(a, b) ，得到 原方程的特解。
• 原方程的全部解为 x + m * C / gcd(a, b)， m∈Z
  • 令 s = C / gcd(a, b)
  • 所以最小的整数解为   (x%s + s) % s

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
typedef long long ll;
// d = gcd(a, b) = ax + by
ll exgcd(ll a, ll b, ll& x, ll& y) {
    ll d = a;
    if(b!=) {
        d = exgcd(b, a%b, y, x);
        y -= (a/b) * x;
    } else {
        x = ; y = ;
    }
    return d;
}
// Ax = B (mod C)
ll solve(ll A, ll B, ll C){
    ll x, y;
    ll d = exgcd(A, C, x, y);
    if(B%d!=){
        return -;  // 无解
    }
    x *= B/d;
    ll s = C/d;
    return (x%s + s)%s;
}
int main()
{
    int A, B, C, k;
    while(scanf("%d %d %d %d", &A, &B, &C, &k)!=EOF && A+B+C+k) {
        ll ans = solve(C, B-A, (ll)<<k);   // A+Cx = B (mod 2^k)
        if(ans==-) {
            printf("FOREVER\n");
        } else {
            printf("%lld\n", ans);
        }
    }
    return ;
}

G - Divisors

题目大意：

求组合数C(n, k)的因子个数。（0 ≤ k ≤ n ≤ 431）

分析及代码：

一看n，k都不大，直接将定义式的连乘项分解，统计每个素因子的出现次数。

然后有那啥公式，每个素因子个数+1后再相乘即为答案，交一发T了。

加上素数筛，还是T了。优化 了下，T了。改对n，k的记忆化，还是T了。

。。。

来学习一下求n!某个因子个数的方法：(去年博客）

 // 公式：cnt = [n/p] + [n/p^2] + [n/p^3] +...+ [n/p^k]

 // 核心代码：

int cnt = ;

while(n) {
　　cnt += n/p;

　　n /= p;

}

终于AC的代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = ;
int cnt[maxn], n, k;
int p[maxn], num;
void init() {
    for(int i=;i<maxn;i++) {
        bool isp = true;
        for(int j=;j*j<=i;j++) {
            if(i%j==) {
                isp = false;
                break;
            }
        }
        if(isp) p[num++] = i;
    }
}

int cal(int n, int p) {
    int res = ;
    while(n) {
        res += n/p;
        n /= p;
    }
    return res;
}
int main()
{
    init();
    while(scanf("%d %d", &n, &k)!=EOF) {
        long long ans = ;
        for(int i=;i<num && p[i]<=n;i++) {  // 没有p[i]<=n TLE!!!
            long long cnt = ;
            cnt += cal(n, p[i]);
            cnt -= cal(k, p[i]);
            cnt -= cal(n-k, p[i]);
            ans *= (cnt+);
        }
        printf("%lld\n", ans);
    }
    return ;
}

H - 青蛙的约会

题目大意：

同F题，求同余方程 x-y + (m-n) * k = 0 (mod L) k的最小正整数解。

分析及代码：

按照F的推导过程慢慢推吧。

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
// d = gcd(a, b) = ax + by
ll exgcd(ll a, ll b, ll& x, ll& y) {
    ll d = a;
    if(b!=) {
        d = exgcd(b, a%b, y, x);
        y -= (a/b) * x;
    } else {
        x = ; y = ;
    }
    return d;
}
// Ax = B (mod C)
ll solve(ll A, ll B, ll C){
    ll x, y;
    ll d = exgcd(A, C, x, y);
    if(B%d!=){
        return -;  // 无解
    }
    x *= B/d;
    ll s = C/d;
    return (x%s + s)%s;
}

int main()
{
    ll x, y, m, n, L;
    cin>>x>>y>>m>>n>>L;
    ll ans;
    if(m>n) ans = solve(m-n, y-x, L);   // m-n>0
    else ans = solve(n-m, x-y, L);
    if(ans==-) {
        printf("Impossible\n");
    } else {
        printf("%lld\n", ans);
    }
    return ;
}

I - Semi-prime H-numbers

题目大意：

定义类似4*k+1的正整数为H数。H数分为两种，H素数和H合数，合数中只能分解成两个H素数相乘形式的为H半素数。

求一个区间内H半素数的个数。

分析及代码：

模仿素数筛的写法，很容易实现O(nlogn)的H素数筛法。

在筛选过程中，将H数为标记为三种类别，素数、半素数、合数。

最后将所有含有半素数标记的取出，采用upper_bound二分查找可以快速得到答案。

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int maxn = ;
int Htype[maxn];    // 0:prime  2:semi-prime  1:composite
//int p[maxn], num;
int pp[maxn], num2;
void init() {
//    Htype[1] = isp[5] = 0;
    for(int i=;i<maxn;i+=) {
        if(!Htype[i]) {
            //p[num++] = i;
            if(i<maxn/i) Htype[i*i] = ;

            for(int j=*i;j<maxn;j+=i) {
                if(j%==) {
                    Htype[j] = ;
                    if((j/i)%== && !Htype[j/i])
                        Htype[j] = ;
                }
            }
        }
    }

    for(int i=;i<maxn;i+=) {
        if(Htype[i]==) {
            pp[num2++] = i;
        }

    }
}

int main()
{
    init();
    int h;
    while(scanf("%d", &h)!=EOF && h) {
        printf("%d ", h);
        printf("%d\n", upper_bound(pp, pp+num2, h) - pp);
    }
    return ;
}

---

(未完待续）