Distance Dependent Infinite Latent Feature Model 阅读笔记1
阅读文献:Distance Dependent Infinite Latent Feature Model
作者:Samuel J.Gershman ,Peter I.Frazier ,and David M.Blei
摘要:
潜在特征模型在对数据进行小模块分解的过程中被广泛使用。这些模型的贝叶斯非参数变量在潜在特征上使用了IBP先验,进而使得特征的数量由数据决定。我们提出了一种一般化的IBP——距离依赖IBP,用来建模不可交换数据。这种模型依赖于数据点之间定义的距离,倾向于使相邻近的数据共享更多的特征。距离测度的选择不同可以带来不同的依赖关系,包括时间和空间。除此之外,original IBP是dd-IBP的特例。我们建立了dd-IBP模型,并从理论上证明了它具有特征共享的特性。我们使用MCMC sampler 求解带有dd-IBP先验的线性高斯模型,并且研究这种模型在实际的不可交换数据中的应用。
- 简介:
很多自然现象可以分解为潜在特征。例如,视觉场景可以被分为物体组合;基因调控网络可以被分解为转录因子;音乐可以被分解为谱段。在这些例子中,很多潜在特征可以同时出现,每一个都能影响观察数据。PCA ,因子分析,以及概率矩阵分解等降维的方法,为我们提供了统计学方法来推断潜在特征。这些方法选择了少量特征或者低维度特征,并把数据点表示成这些特征的加权组合。维度的降低可以提高预测的准确度,并得到观测数据中的隐藏结构。
维度降低的方法通常要求潜在特征的数量要事先固定。学者们 最近提出了一种更灵活的方法,这种方法基于贝叶斯非参数模型,好处在于,特征的数量通过后验分布从数据中推断得到。这些模型通常基于IBP【16.17】,IBP是一个二值矩阵上的先验,这个二值矩阵有有限行(行数与数据点个数相同)无限列(潜在特征的个数)。使用IBP作为建筑模块,贝叶斯非参数模型在很多的统计问题中有应用,如【18,19,21,22】。由于潜在特征 的个数是不确定的,所以这些模型经常被称作是无穷维潜在特征模型。
IBP假设数据是可交换的,即重新排列行(数据点)的顺序不会改变潜在特征分配的概率。这个假设在某些数据集中适用,但是对于其他的一些情况,我们希望数据点之间有依赖关系进而能在潜在的表示中得到依赖关系。例如,用来描述人类运动的潜在特征应该与时间相关;描述环境风险因子的潜在变量应该与空间相关。在本文中,我们提出了一种更一般化的IBP——dd-IBP,用来强调上文提到的这种约束。dd-IBP 采用无穷维的潜在特征的模型来建模不可交换的结构。
使非参数模型适应不可交换数据的问题在混合模型的相关文献中也是研究热点。尤其是在一些狄里克雷过程混合模型中,其变量可以用来建模数据点之间的依赖关系,如【1.6.8.11.15.23】。这些依赖关系可以是时间的,也可以是空间的,甚至是一些更一般的协同相关性;这些相关性的后果就是使得相邻数据间共享潜在特征。
dd-CRP是其中之一,它是中餐馆模型的一种不可交换的一般化模型。dd-CRP 建模这种不可交换性用的方法是通过数据点之间的距离,即相邻的数据点更有可能被分到同一个混合成分中去。而dd-IBP 将这种思想延伸到了潜在特征模型中去,这里的数据点之间的距离影响的是特征的分享,即相邻的数据点更有可能分享共同的潜在特征。、
我们将在2.1中回顾IBP,并在2.2中给出dd-IBP的定义,和dd-CRP一样,dd-IBP也不具有边缘分布不变性,也就是说,删除一个观测值将会改变其他所有观测值的联合分布。我们在2.3中讨论这条性质。尽管很多贝叶斯非参数模型符合这条性质,但是这将是一个针对某些问题的特殊模型。
还有其他的一些无穷维潜在特征模型用不同的方法来解决数据之间的依赖问题,例如,使用进化树的方法或者隐高斯过程的方法。与本文工作最相近的是分层依赖beta过程(dHBP)【30】,这些相关的模型将在第三节中讲到。在第四节中我们将会讨论dd-IBP的特征共享特性并与dHBP相比较。我们发现不同的模型建模了性质上不同的依赖结构。
dd-IBP的后验推断很复杂,在第五节中,我们提出了一种基于MCMC的近似推断算法。在第六节中,我们用这种算法来推断线性高斯模型的潜在特征。然后在第七节中我们用dd-IBP建模人类大脑图像数据,并且从不同的 个体之间的依赖关系中学习预测年龄。这表明dd-IBP 能产生对监督分类有重要作用的特征。
- 距离依赖印度餐馆过程
- IBP
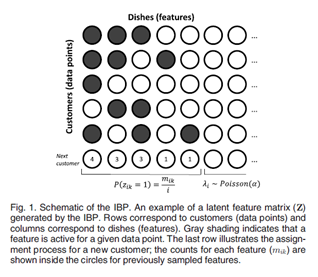
IBP 是在一个有无穷列的矩阵上的先验。在印度餐馆过程的比喻中,Z的行代表着顾客,Z的列代表着菜品(Fig.1)。在数据分析时,顾客代表数据,菜品代表特征。使用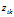 代表Z的第i 行,第k 列。顾客i 是否选择菜品k表示数据i 是否拥有特征k 。
代表Z的第i 行,第k 列。顾客i 是否选择菜品k表示数据i 是否拥有特征k 。
IBP定义了一个序贯过程。第一个进入餐馆的顾客选择最开始的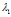 个菜品,其中
个菜品,其中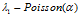 ,这里的超参数
,这里的超参数 是一个尺度因子。在二值矩阵中,这代表着第一行的相邻的
是一个尺度因子。在二值矩阵中,这代表着第一行的相邻的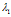 个1,其余的无穷个都是0。
个1,其余的无穷个都是0。
接下来的顾客i=2,3,…,N 进入餐馆,并选择之前选过的菜品的概率是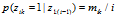 ——(1)这里的
——(1)这里的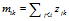 是在i之前选了菜品k的顾客数量。然后每个顾客采
是在i之前选了菜品k的顾客数量。然后每个顾客采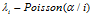 个新菜品。同样的,这些新菜品代表了在之前的顾客采样的菜品后面的一段连续的1 。
个新菜品。同样的,这些新菜品代表了在之前的顾客采样的菜品后面的一段连续的1 。
尽管这个过程的表述是序贯的,但是【16】证明了IBP所定义的这种顾客的菜品配置是可交换的。也就意味着进入餐馆的顺序不会影响菜品对顾客的配置分布。
为了标准化记号,定义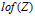 :是一个通过以下过程得到的左序二值矩阵,它是把Z的列按降序排列,把每一列看作一个整数,这个整数代表了在第一行表示最高位的二进制数。(通俗的讲是这样的,把每一列的看成一个二进制表示的整数,第一行表示了它的最高位,然后把这些整数降序排列,得到新的矩阵就叫做左序二值矩阵。)然后定义了集合
:是一个通过以下过程得到的左序二值矩阵,它是把Z的列按降序排列,把每一列看作一个整数,这个整数代表了在第一行表示最高位的二进制数。(通俗的讲是这样的,把每一列的看成一个二进制表示的整数,第一行表示了它的最高位,然后把这些整数降序排列,得到新的矩阵就叫做左序二值矩阵。)然后定义了集合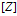 :满足
:满足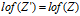 的
的 二值矩阵Z'的集合。这个矩阵与表示了特征与顾客分配关系的矩阵含义是相同的,只是在特征的标号上有所不同。菜品对顾客的IBP配置的可交换性意味着随机等值类别
二值矩阵Z'的集合。这个矩阵与表示了特征与顾客分配关系的矩阵含义是相同的,只是在特征的标号上有所不同。菜品对顾客的IBP配置的可交换性意味着随机等值类别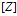 的分布与重新对行进行调整之后的
的分布与重新对行进行调整之后的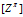 的分布是相同的。在下一部分我们提出了一种更一般的IBP可以松弛这个假设。
的分布是相同的。在下一部分我们提出了一种更一般的IBP可以松弛这个假设。
- DD-IBP
类比于IBP,dd-IBP也是在有限行无穷列的二值潜在特征矩阵上的分布。每一对顾客有一个相应的距离,例如时间或者空间距离,或者依赖于一个协变量的距离。在某种距离定义下更近的两个顾客可能共享相同的菜品(特征)。
dd-IBP可以通过下面的序贯过程来理解。首先,每一个顾客选择的菜品数量服从一个服从泊松分布,在这里,我们把这个过程描述为顾客"拥有"这些菜品(特征)。每个菜品对一个顾客来说只能存在有与没有两种状态,这个过程和IBP中选择新菜品相似。
然后,对于每一个被拥有的菜品,顾客与其他拥有该菜品的顾客相连。一个顾客与其他顾客相连的概率随着距离的增长而减小。顾客并不采样每一个菜品,但是相反的链接到每个顾客上。因此每个菜品通过顾客之间的链接图来分配。
顾客的这些per-dish 图决定了菜品继承:如果在一个菜品连通图中这个菜品的所有者和当前顾客是可连接的,那么当前顾客将会继承这个菜品。这种继承关系是通过在之前步骤中生成的连接关系明确计算的。每个顾客所拥有的菜品是它从别人那里继承的加上他自身拥有的。因此,距离依赖连接概率表示了相邻顾客之间菜品采样的相似性。
在Fig.2中给出了一个从dd-IBP中采样得到的顾客配置的例子。在这个例子中,顾客1拥有菜品1,顾客2-4通过直接或者间接的方式连接到顾客1,进而继承了菜品1,结果特征1在顾客1-4上都处于激活状态。菜品2由顾客2拥有,只有顾客1与顾客2有通过菜品2的链接,并共享菜品2。菜品3由顾客2拥有,但是没有其他的顾客通过菜品3与顾客2相连,这样菜品3只有在顾客2被激活。(注意这里两个顾客的链接并不是固定的,而是通过不同的菜品会有不同的链接)
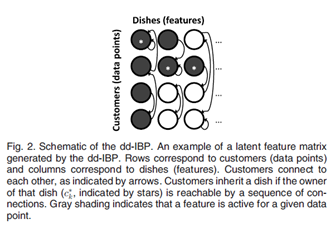
接下来更加规范的描述二值矩阵Z的概率生成过程。先给出一些记号和术语:
·菜品(Z的列)由自然数 来定义。顾客i所拥有的菜品数量是
来定义。顾客i所拥有的菜品数量是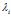 ,菜品按顺序排列,因此顾客拥有的菜品的集合是
,菜品按顺序排列,因此顾客拥有的菜品的集合是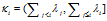 。总的菜品数是
。总的菜品数是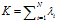 。除了顾客i以外其他的顾客所拥有的菜品集合是
。除了顾客i以外其他的顾客所拥有的菜品集合是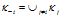 。(注意最后一个是集合不是数量)
。(注意最后一个是集合不是数量)
·每个菜品都有一个对应的customer-customer的分配,用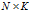 的连接矩阵C表示,
的连接矩阵C表示,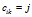 表示顾客i在菜品k上与顾客j相连。如果已知C,顾客形成了一个有向图的集合,每个菜品都有一个。所属关系向量记为
表示顾客i在菜品k上与顾客j相连。如果已知C,顾客形成了一个有向图的集合,每个菜品都有一个。所属关系向量记为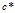 ,长度为K,这里的
,长度为K,这里的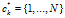 表示拥有菜品k的顾客,因此
表示拥有菜品k的顾客,因此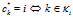 。
。
·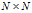 的距离矩阵记为D,顾客i与j之间的距离记为
的距离矩阵记为D,顾客i与j之间的距离记为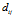 。每个顾客与自己的距离是0(最近的)。当j>i时,令
。每个顾客与自己的距离是0(最近的)。当j>i时,令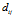 =0,我们得到了序贯的距离矩阵,在这种情况下,顾客只能链接到之前出现的顾客。
=0,我们得到了序贯的距离矩阵,在这种情况下,顾客只能链接到之前出现的顾客。
·衰减函数: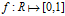 将距离转换为了质量,我们叫做proximity,控制了相连顾客的概率。条件:
将距离转换为了质量,我们叫做proximity,控制了相连顾客的概率。条件: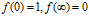 。通过将衰减函数应用到每一个顾客链接上,并进行归一化,得到了归一化的距离矩阵A。这里
。通过将衰减函数应用到每一个顾客链接上,并进行归一化,得到了归一化的距离矩阵A。这里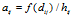 ,
,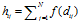 .
.
使用上述记号,我们生成了以下关于特征索引的矩阵Z:
- 分配菜品所有关系。对于每一个顾客令
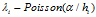 并且令集合
并且令集合 ,为这个顾客分配了
,为这个顾客分配了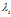 个菜品。对于每个
个菜品。对于每个 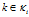 ,记
,记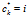 。
。 - 分配顾客链接。对每一个顾客i和菜品
 ,根据
,根据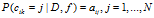 ,采样一个顾客链接。同时顾客可以连向自己。在这种情况下它不继承菜品除非他拥有。
,采样一个顾客链接。同时顾客可以连向自己。在这种情况下它不继承菜品除非他拥有。 - 计算菜品继承关系。如果对于菜品k 存在一条从顾客j到菜品k的拥有者
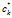 的沿着有向图的通路(这个有向图在是由C的第k列定义的),那么我们就认为顾客j继承了菜品k。这个菜品的拥有者自动算作是继承者。我们用L来表示联通性,即如果在菜品k上顾客i和顾客j是可联通的,那么记为
的沿着有向图的通路(这个有向图在是由C的第k列定义的),那么我们就认为顾客j继承了菜品k。这个菜品的拥有者自动算作是继承者。我们用L来表示联通性,即如果在菜品k上顾客i和顾客j是可联通的,那么记为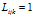 ,否则记为0.
,否则记为0. - 计算特征索引矩阵。对每一个顾客i和菜品
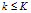 ,如果i继承了菜品k,记
,如果i继承了菜品k,记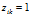 ,否者
,否者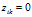 ,对所有的k>K,
,对所有的k>K, 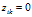 。
。
dd-IBP 的生成过程定义了关于所属向量和连接矩阵的联合概率分布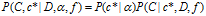 ,
,
考虑其中的第一项,所属向量的概率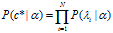 ,其中c*是
,其中c*是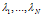 的deterministic function。
的deterministic function。
考虑其中的第二项,连接矩阵C的条件概率由菜品数量的总和和规范化的近邻矩阵A决定,其中A是由距离和衰减函数推导得来: ,依赖关系c*来源于K,K是由所属关系向量c*决定的。
,依赖关系c*来源于K,K是由所属关系向量c*决定的。
随机特征模型(传统的IBP)在一个随机二值矩阵及其所诱导得出的特征分配上进行操作。在dd-IBP中,Z是随机变量C和c* 的确定的多对一函数,记作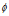 。我们通过边缘化这些变量的适当结构来计算二值矩阵的概率,
。我们通过边缘化这些变量的适当结构来计算二值矩阵的概率,
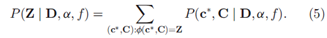
当
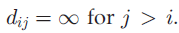 ,
,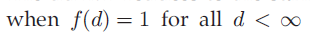
dd-IBP退化为IBP.
为了说明这个过程,做如下解释:考察在第k个菜品在顾客i之前已经被采样的条件下,该菜品又被顾客i 采样的概率。这个概率正比于已经连接到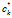 的顾客的数量——因为连接到每个顾客的概率是1。概率的只是是
的顾客的数量——因为连接到每个顾客的概率是1。概率的只是是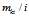 ,与IBP中的相同。这与dd-CRP与CRP 的关系是相同的。
,与IBP中的相同。这与dd-CRP与CRP 的关系是相同的。
很多不同的衰减函数可以应用到这个框架中。Fig.3展示了四个衰减函数在Z的采样中的应用。
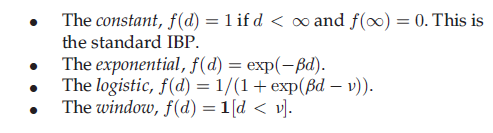

每个衰减函数用不同的方式给出了相邻行之间的特征共享关系。
当和观测模型——指定了潜在特征和观测数据之间的关系——结合到一起的时候,dd-IBP 函数作为数据集的潜在特征表示上的先验。在第六部分中我们指出了如何将dd-IBP 应用在分析现实数据中。
2.3边缘不变性与可交换性
现在来讨论dd-IBP与IBP在理论上的一些不同。与传统的IBP 不同,dd-IBP不具有边缘不变性,所谓的边缘不变性指的是删除一个顾客将不会改变剩下的顾客在潜在特征上的分布。在某些情况下,边缘不变性有很大的计算需求。例如,对于不具有边缘不变性的模型来说,缺失数据的条件分布需要计算规范化常数。相反,对于具有边缘不变性的模型来说,由于他们的因式分解结构(应该是指独立连乘的结构)那么对缺失数据的条件分布的计算更简洁一些。在一些其他的情况中,如对整个数据集进行探索性分析,这样的情况中计算难易并不重要。
除了计算考虑,在某些场景中边缘分布不变性的假设是不合适的。例如,在研究病毒的传播时,你坚信潜在特征存在,并且在病毒传播过程中扮演着重要角色。这种情况中,观测值与个体相关,并且距离会自然的依照家庭图谱来计算。从一个家庭树图中删除一个个体会严重地改变在同一个家庭树中其他个体的基因分布。这是一个不适用边际不变假设的例子。相反,个体间基因的距离依赖影响可以通过在dd-IBP中合理地使用距离函数而进行建模。
与传统IBP 的另外一个不同是,普遍的dd-IBP 的特征分配是不可交换的,有些特殊情况除外。为了正式地描述这种情况,Z从距离矩阵为D,权重alpha,衰减函数f的dd-IBP 过程中采样。然后,记π为整数排列,记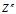 是由Z按照π的顺序重新排列之后得到矩阵,那么在一般情况下这二者是不相等的
是由Z按照π的顺序重新排列之后得到矩阵,那么在一般情况下这二者是不相等的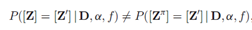 。也就是说重新排列数据是会改变分布的,因此普遍的dd-IBP的特征配置是不具有可交换性的。这种性质来源于距离矩阵,因为距离矩阵表示了数据点之间的序贯依赖性。
。也就是说重新排列数据是会改变分布的,因此普遍的dd-IBP的特征配置是不具有可交换性的。这种性质来源于距离矩阵,因为距离矩阵表示了数据点之间的序贯依赖性。
尽管dd-IBP不具有分布可交换性,但是却有一个与此相关的对称性:记 为N*N矩阵,是将D的行和列都按照π重新排列之后得到的。
为N*N矩阵,是将D的行和列都按照π重新排列之后得到的。 那么就是说,如果我们同时重新排列数据和距离矩阵,概率仍然是不变的。二者都重新排列,相当于对数据进行重新标记,概率分布也会随着新的标记而改变。如果dd-IBP的特征分布是可交换的,我们就不需要改变根据新的标记改变概率分布。
那么就是说,如果我们同时重新排列数据和距离矩阵,概率仍然是不变的。二者都重新排列,相当于对数据进行重新标记,概率分布也会随着新的标记而改变。如果dd-IBP的特征分布是可交换的,我们就不需要改变根据新的标记改变概率分布。
- 相关工作
这个部分主要讨论与无穷维潜在特征模型相关的一些能够建立数据间外在依赖关系的模型。最相近的是依赖分层beta过程【DHBP ,30】.作为DHBP的前奏,我们讨论IBP与beta process 之间的联系。
- Beta 过程
文献【27】指出在IBP下的De Finetti混合分布就是beta process,参数是一个正的集中度参数c和一个在Ω上的基本测度 ,从可计数的无穷维权重原子集合中采样分布
,从可计数的无穷维权重原子集合中采样分布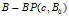 ,式子为
,式子为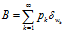 这里的
这里的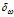 是一个概率分布,这个概率分布是在
是一个概率分布,这个概率分布是在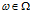 处的一个原子分布。
处的一个原子分布。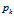 是一个独立随机变量,它的分布将在下面进行介绍。如果基分布是连续的分布,那么原子和它们的权重是从一个非均匀(非齐次)的Possion 过程中采样的,Poisson 过程是定义在Ω空间上的,rate measure是
是一个独立随机变量,它的分布将在下面进行介绍。如果基分布是连续的分布,那么原子和它们的权重是从一个非均匀(非齐次)的Possion 过程中采样的,Poisson 过程是定义在Ω空间上的,rate measure是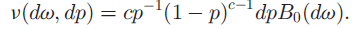 ,如果基分布是离散的,形式为
,如果基分布是离散的,形式为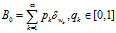 ,那么B也会与
,那么B也会与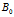 用有同样的原子成分,权重
用有同样的原子成分,权重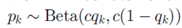 按照【27】的做法,我们定义质量参数为
按照【27】的做法,我们定义质量参数为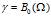 .由于
.由于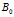 不是必须符合概率测度的要求,所以
不是必须符合概率测度的要求,所以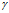 可以取和1不同的非负值。
可以取和1不同的非负值。
在beta process 的采样条件下,数据i的特征表示 是从基分布为B的贝努力过程中采样得到的:
是从基分布为B的贝努力过程中采样得到的: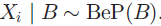
如果B是离散的,那么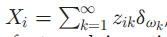 其中
其中 。换句话说,特征k是独立于所有数据点以概率pk激活的。当
。换句话说,特征k是独立于所有数据点以概率pk激活的。当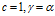 时,从混合的beta-bernoulli 过程中采样Z和直接从IBP中采样Z是相同的。
时,从混合的beta-bernoulli 过程中采样Z和直接从IBP中采样Z是相同的。
(尝试记录两个平行过程的等价性图解)
- DHBP
Dhbp使在BP构造的基础上建立了数据点之间的外在依赖关系。这种依赖关系由混合不独立的BP随机测度诱导,权重是他们的亲和度矩阵A。
DHBP 遵从下列产生式过程:
这个过程等价于:从一个基分布为BP随机测度线性组合的贝努力过程中采样,即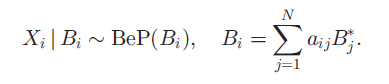
数据点之间的依赖关系在DHBP中由亲密度矩阵A表示,这和DD-IBP是一样的。这个性质是的相邻的数据点之间更有可能共享潜在的特征。
在第四节中我们会比较DD-IBP与DHBP的特征共享性质。通过渐进分析,我们发现DD-IBP在建模数据点之间的特征共享的性质上有更松弛的性能,但是在建模不确定性时松弛性能并不如DHBP.
- 其他 的不可交换变体
这里讨论几个其他的对无限潜在特征模型的不可交换性质的先验【14】。【28】中提出了一种使用协变量依赖的方式通过分层高斯过程组织潜在特征。他们把这个模型命名为依赖IBP。他们的模型是很灵活的:可以根据行来连接Z的列(这在dd-IBP中是做不到的)。但是这种灵活性也带来了推断过程中的计算消耗:他们的算法需要采样一层额外的变量。
【20】中提出了一种遗传进化的IBP,这种算法能够编码数据之间的树状结构的依赖关系。【10】中提出一个相关性IBP,通过潜在聚类来划分数据点和特征。这些模型都放宽了可交换性的约束,但是他们不允许根据数据间的距离直接指定依赖关系。而且,这些模型的推断比标准的IBP需要更多的计算资源。【20】中提出的MCMC 算法不仅需要动态编程还需要辅助变量的采样。同样相关性IBP的MCMC算法也需要采样潜在团簇。我们的算法相比于传统的IBP也需要耗费额外的计算资源,因为要计算链接性(计算复杂度是观测数据个数的平方)。然而,相比于上面的两个模型,我们的模型能够允许有更多的明确的数据之间的依赖结构。
最近,【25】提出了一种新颖的方法:通过beta 过程把依赖关系引入潜在特征模型。不再定义顾客之间的距离,而是把每个菜品关联到一个潜在的协变量向量上,距离被定义在顾客的协变量和菜品种类的协变量上。这样顾客就根据正比于顾客-菜品亲和度的概率来选择菜品,这种构造有这明显的计算优势,时间复杂度正比于观测数据的个数上。这种构造的缺陷在于,用来推断的MCMC方法必须为每一个菜品采样一个独立的协变量向量,当这个协变量维度过高时很难计算。
4 描述特征共享的特性
在这一部分,我们将要讨论DHBP和DD-IBP的特征共享的特性。如果数据点的同一个特征都被激活(即对于一个已经有的特征k,当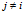 时,
时,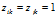 )我们就说两个数据点共享一个特征。这个性质的分析有助于我们去理解不同的模型所定义的依赖关系,也有利于在分析不同的数据时进行模型选择和超参数设置。我们考虑一种权重参数很大的近似情况,这大大地简化了特征共享的性质。所有命题的证明在附录中都有。
)我们就说两个数据点共享一个特征。这个性质的分析有助于我们去理解不同的模型所定义的依赖关系,也有利于在分析不同的数据时进行模型选择和超参数设置。我们考虑一种权重参数很大的近似情况,这大大地简化了特征共享的性质。所有命题的证明在附录中都有。
4.1dd-IBP中的特征共享特性
我们先来描述当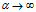 时,有限分布的特征共享的性质。我们从可达性索引矩阵
时,有限分布的特征共享的性质。我们从可达性索引矩阵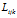 中去掉特征索引k,也就是针对某一个特征k进行讨论,它的可达性矩阵变成二维的
中去掉特征索引k,也就是针对某一个特征k进行讨论,它的可达性矩阵变成二维的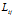 。我们这样做是因为连接矩阵C在DD-IBP下是一个确定的分布,随机向量是对k具有不变性。
。我们这样做是因为连接矩阵C在DD-IBP下是一个确定的分布,随机向量是对k具有不变性。
用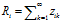 表示顾客i拥有的特征的个数,
表示顾客i拥有的特征的个数, 表示i和j共同拥有的顾客的数量。
表示i和j共同拥有的顾客的数量。
命题1 在dd-IBP的假设下,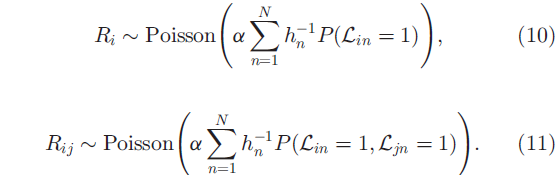
命题中的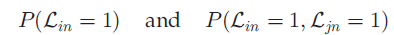 与连接矩阵C有密切关系,但由于L与菜品的所有关系之间是相对独立的,所以L与c*无关。
与连接矩阵C有密切关系,但由于L与菜品的所有关系之间是相对独立的,所以L与c*无关。
接下来我们根据Poisson 分布的性质,用上述结果推导两个R的极限性质
命题2
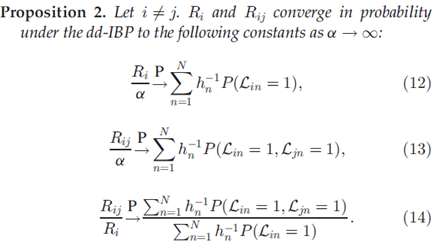
这个命题表明,DD-IBP中的共享特征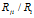 的极限分数是一个常数,这个常数对于每一对点i和j是不同的。相对应的,我们将在下面说明这个极限分数在DHBP中是从两者之中随机取一个。这两个值是固定的,不随ij改变。
的极限分数是一个常数,这个常数对于每一对点i和j是不同的。相对应的,我们将在下面说明这个极限分数在DHBP中是从两者之中随机取一个。这两个值是固定的,不随ij改变。
4.2DHBP中的特征共享
这里描述在B无限集中(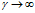 )的情况下,DHBP特征共享的极限分布特性。在这种极限条件下,特征共享主要是由于由亲密度矩阵A带来的依赖关系。
)的情况下,DHBP特征共享的极限分布特性。在这种极限条件下,特征共享主要是由于由亲密度矩阵A带来的依赖关系。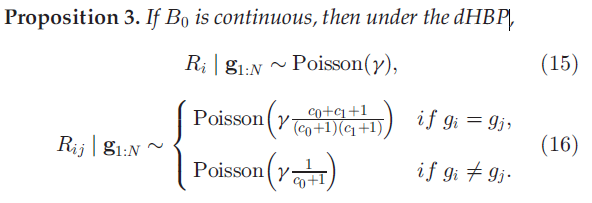
我们从Poisson 分布的性质中推导出R的极限性质。
命题4. 假设B是连续的,在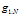 的条件下有:
的条件下有: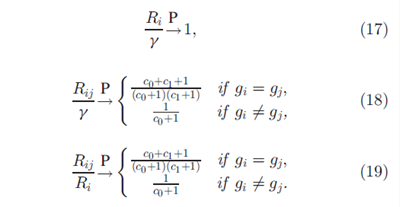 因此,在gi=gj时,i 和j 共享特征的期望分数是一个比
因此,在gi=gj时,i 和j 共享特征的期望分数是一个比 稍大一点儿的数。当
稍大一点儿的数。当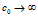 时,这个分数趋于无穷当
时,这个分数趋于无穷当 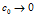 时,这个分数趋于1.我们通过边缘化gi和gj得到没有条件的分数:
时,这个分数趋于1.我们通过边缘化gi和gj得到没有条件的分数:

这个引理表明,随着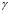 的增大,这个分数会成为两个之中的一个。因此,DHBP确实具有灵活性,但是它最终只被两个极限值所限制。
的增大,这个分数会成为两个之中的一个。因此,DHBP确实具有灵活性,但是它最终只被两个极限值所限制。
4.3 在IBP中的特征共享特性
为了对比,简单地描述一下在传统IBP的条件下特征共享的性能。
在传统IBP中 ,由于Z的对等类别的可交换性,并且在同一个对等类别中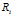 与
与 对所有的Z都是相同的,所以
对所有的Z都是相同的,所以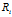 与
与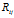 和
和 与
与 具有相同的联合分布。第一个顾客采样了
具有相同的联合分布。第一个顾客采样了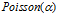 个菜品,第二个顾客要么以1/2的概率独立地选择已有的菜品,这时,第一个顾客和第二个顾客共同选择的菜品数是
个菜品,第二个顾客要么以1/2的概率独立地选择已有的菜品,这时,第一个顾客和第二个顾客共同选择的菜品数是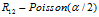 。
。
这表明在传统的IBP中,当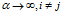 时:
时:
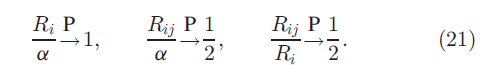
4.4讨论
应用渐进的分析,前面的理论的结果已经表明DDIBP和DHBP在解释数据点之间共享特征的方法上有不同形式的灵活性。这个渐进分析时在权重参数趋于无穷大的极限下进行讨论的。这个极限是在理论上易行的,并且去掉了一些在这个模型中可能发生的不确定性。尽管这种极限的DDIBP和DHBP是实际应用中是不存在的,但是他们的简洁性为非渐进情况的表现提供了思考方向。
在DDIBP中,命题2说明,这个模型允许在通过数据指定特征共享比例时有很大的灵活性。如果有一个矩阵可以指定在数据点对之间共享的特征的比例,那么我们就可以设计一个距离矩阵,这个距离矩阵能使得DDIBP集中到期望的比例上。尽管DDIBP不能建模一个任意指定的比例矩阵,但是能够建模的矩阵也不在少数。
相对的,在DHBP中,引理1表明,在建模共享特征比例是的灵活性要小一些。在DHBP中了,只有两个可能值作为候选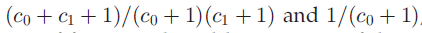 。
。
在4.3中看到,传统的IBP不具有太大的灵活性,在渐进的情况中,在数据点对之间共享特征的比例是一个常数。
尽管在解释特征共享比例的数值时DDIBP有更多的灵活性,但是在建模特征共享比例的不确定灵活性要差一点。在DDIBP中,特征共享的比例在极限条件下是特定的值,在DHBP中,这个比例是一个随机的值,即使是在渐进的情况下。我们可以扩展DDIBP,特征共享比例的不确定性可以通过指定一个距离矩阵的超先验来完成,但在本文不做讨论。(一个可以前进的方向)

Fig4 说明了DHBP与DDIBP在渐进的特征共享中的不同。这里使用的指数衰减函数,指数函数中参数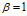 ,距离使用的是欧式距离
,距离使用的是欧式距离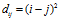 。上面一行的子图是从DHBP中采样得到的,下面是从DDIBP 中采样的得到的。在每个图像中,cell(i,j)上的阴影表示
。上面一行的子图是从DHBP中采样得到的,下面是从DDIBP 中采样的得到的。在每个图像中,cell(i,j)上的阴影表示 (对角线上是
(对角线上是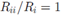 ,被置0了)。每一列代表了一组独立采样,为了近似理论中的渐进情况我们把参数调到很大的值
,被置0了)。每一列代表了一组独立采样,为了近似理论中的渐进情况我们把参数调到很大的值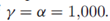
如图所示,在DHBP的采样中可以看到,非对角线元素取值有两个。在不同的列中有不同的分布模式,这说明 的取值是随机的。相反,在DDIBP中,非对角线元素的取值有很多种,但是四列的分布都是相同的不具有随机性。
的取值是随机的。相反,在DDIBP中,非对角线元素的取值有很多种,但是四列的分布都是相同的不具有随机性。
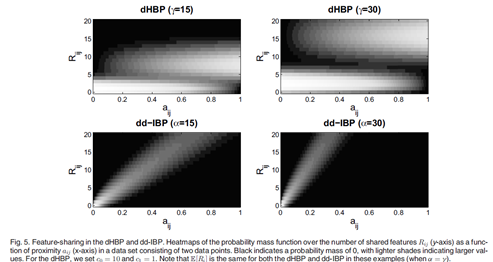
Fig5,说明了在只有两个点的简单集合中非极限情况的特征共享特性。图中表示了DHBP和DDIBP的在权重系数的两个值上的特征共享特性。每一个子图把概率权重矩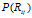 看成是亲密度矩阵
看成是亲密度矩阵 的函数,在DDIBP中,
的函数,在DDIBP中,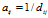 。由于只有两个数据点,
。由于只有两个数据点,
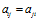 知名了aij 就指明了亲密度矩阵A,对于DHBP来说,我们把
知名了aij 就指明了亲密度矩阵A,对于DHBP来说,我们把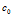 设置为10,c1设置1.为了便于比较,在两个模型中
设置为10,c1设置1.为了便于比较,在两个模型中 的期望是相同的。
的期望是相同的。
Fig.5表明,当亲密度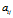 逐渐增长至1时,共享特征数目在两个模型中都有增长的趋势。更准确地说,是随着
逐渐增长至1时,共享特征数目在两个模型中都有增长的趋势。更准确地说,是随着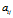 的逐渐增长,
的逐渐增长,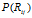 集中在更大的
集中在更大的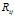 上。然而,在两个模型中概率密度函数的增长方式有所不同。在DDIBP中,增长的更加平滑,在 DHBP中增长的具有跳跃性。在所有取值范围内改变
上。然而,在两个模型中概率密度函数的增长方式有所不同。在DDIBP中,增长的更加平滑,在 DHBP中增长的具有跳跃性。在所有取值范围内改变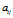 ,在DDIBP 中
,在DDIBP 中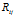 在整个区域(0~20)进行变动。然而DHBP中只取几个值。改变DHBP中的
在整个区域(0~20)进行变动。然而DHBP中只取几个值。改变DHBP中的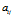 带来很多的双峰分布,双峰分布的中心是在极限分析的值附近。
带来很多的双峰分布,双峰分布的中心是在极限分析的值附近。
在非极限情况下表现的不同反映了两个模型在极限情况下的不同。DDIBP可以带来任意的特征共享比例值,但是在不确定性上不具有灵活性。而DHBP限制了可能取值的数量,却有着更好的不确定性。这在很多的数据分析中有用。例如,在电影或者音乐中的潜在特征可能以一种很有确定性但是完全不同的方式从一个个体的集合中被共享,这种情况下DDIBP就可能是一个更好的模型。相反的,在传染病预测中,潜在特征就可能以很少的途径但有很大的不确定性的方式进行共享,这种情况下DHBP可能更有效。
5.应用MCMC的方法进行模型求解
已知数据集 和潜在特征模型
和潜在特征模型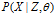 ,推断的目标是通过贝叶斯规则在顾客配置矩阵,DDIBP超参数
,推断的目标是通过贝叶斯规则在顾客配置矩阵,DDIBP超参数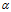 和似然参数
和似然参数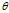 上,计算联合的后验分布。
上,计算联合的后验分布。
这里的第一项式似然,第二项是参数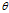 的先验,第三项在链接矩阵C上的DDIBP先验,第四项是在所属关系矩阵c*上的先验,最后一项是参数
的先验,第三项在链接矩阵C上的DDIBP先验,第四项是在所属关系矩阵c*上的先验,最后一项是参数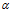 上的先验。
上的先验。
精准的推断面临着很大的计算困难,所以我们采用了【20】中的方法,用L采样来近似后验。细节在附录中,可以在线获取。这个算法可以应用在不同的数据集上,但要选择合适的似然函数。在下一部分我们举一个简单的线性高斯模型的例子。
6.线性高斯模型
作为一个DDIBP在数据分析中的例子,我们把它结合到线性高斯隐特征模型中去,如下图所示,最初在【16,17】中有应用
观测数据X有N个object,每一个都是M维向量(代表了真实特性)。我们把X建模成一个二值隐特征的线性组合,同时引入高斯噪声。
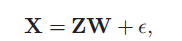
这里的W是K*M的权重矩阵,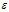 是N*M的矩阵,是独立的,均值为0,标准差为
是N*M的矩阵,是独立的,均值为0,标准差为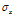 的高斯噪声。我们在W上设置了零均值协方差为
的高斯噪声。我们在W上设置了零均值协方差为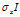 的 高斯先验。直观的,权重决定了潜在特征如何构成观测数据。例如,如果每个潜在特征代表图像中的一个人,那么权重
的 高斯先验。直观的,权重决定了潜在特征如何构成观测数据。例如,如果每个潜在特征代表图像中的一个人,那么权重 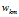 代表了这个人k对像素点m的贡献。相关的算法细节在附录中给出。
代表了这个人k对像素点m的贡献。相关的算法细节在附录中给出。
7.实证研究
在这一部分,我们报告DDIBP的实验结果以及和相关算法的比较。这里指出,当数据不具有交换性的时候,DDIBP可以作为分类之前的一种降维的预处理方法。在附录中,我们提供了一个场景的例子,在这个场景中,不可交换模型本可以有所提高,但实际中却没有。
监督学习算法的性能的提高方法之一是在预处理数据时对特征进行降维。经典的降维方法,如PCA或者因子分析,假设数据具有可交换性,这与基于IBP的无穷维潜在特征模型是相似的。因此,这些技术对不可交换数据的预处理可能就不会有太好的结果,进而会影响到分类效果。
我们用一组MRI数据来验证这个假设,这组数据中包含了27个老年痴呆病人和35个正常人的核磁共振图像。观测特征包含在56个脑区测量的4个经过结构性汇总的统计数据:1.表面区域;2.形状索引;3.曲线;4.分形维数。这个分类任务就是根据他们的观测特正把个体分类到老年痴呆或者正常的类别中去。
与年龄相关的脑结构的改变会造成认知功能的减退,这使得老年痴呆的诊断十分困难。因此,在建立预测模型的时候就很有必要把年龄考虑进去。对于DDIBP 和DHBP,年龄被作为协变量,我们在协变量上构造一个距离矩阵。定义一个序贯的距离矩阵,在i和j之间的距离是年龄的差别(当j>i时距离被定义为无穷大)。这个代表了一个先验就是年龄相近的个体之间会有更多的相似的潜在特征。
具体来说,我们使用线性高斯观测模型在全数据集上运行了1500次MCMC采样,然后选择后验最大的采样值的潜在特征输入监督学习算法。一半数据做训练一半数据做测试。噪声的超参数使用MH proposals进行更新。
我们使用联合分布的log值做检测。可视化结果显示采样在400-500次迭代的时候到达局部最大值。当使用指数衰减函数时,对于某一范围内的衰减系数值这个过程会出现重复。在DDIBP和DHBP中使用相同的亲密度矩阵A.进行了十次不同先验的随机初始化,在每次不同的初始化之后都重新进行分类,对分类结果进行平均来减少采样所带来的随机性。为了进行对比,也使用了IBP,dIBP,以及原始数据进行对比。DIBP使用了【28】中所描述的MCMC采样方法,这种方法对控制观测值之间距离的参数进行可适应性地采样。
Fig8展示了推断得到的潜在特征,表明了特征分布随协变量值的变化情况。在这种情况下,用来解释年龄相对较小的老年痴呆患者数据的潜在特征集合与年龄相对较大的有很大的区别。
在Fig9中给出了相关的分类结果,用ACU来表征结果。在0.5时是偶然的情况,较好的情况相对应的ACU值是1。使用不可交换模型得到的特征比IBP和原始数据要好一些。对于一个范围内的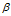 ,DDIBP能够得到比其他模型好很多的分类效果,但是在某些集合上DIBP会好一点。
,DDIBP能够得到比其他模型好很多的分类效果,但是在某些集合上DIBP会好一点。
我们也把DDIBP中的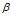 设置为0,发现在这个老年痴呆患者的分类问题上,二者并没有太大的区别。
设置为0,发现在这个老年痴呆患者的分类问题上,二者并没有太大的区别。
8.结论
同过对无穷维潜在特征模型的可交换性假设条件的放宽处理,DDIBP拓展了该模型在更丰富的数据上的应用。我们从实验上展示了在不可交换数据集上新的方法比标准的IBP要好。
这里也指出,从DDIBP是起源于de Finetti 混合分布的方面来讲,ddIBP不是标准的贝叶斯非参数分布。对于标准的IBP,de Finetti 混合分布是beta过程,但是这个结果不能推广到DDIBP上,因为它具有不可交换性。但这并不降低我们模型在从数据中推断潜在特征个数的能力,这种能力是和其他的无穷维潜在特征模型共享的。
我们可以探讨的几个发展方向。首先,我们可以探索距离依赖来驱动更有效的采样。尤其是在文献【9】当中提出,将数据分成子块能够加速传统IBP的采样速度;窗口衰减函数能给出一个对数据自然的划分,把数据划分为条件独立的子集。其次,我们可以把DDIBP应用到其他的似然函数上。例如,可以应用到关系数据【19,21】或者文档数据【27】。在【21】中指出,在连接预测中诸如年龄位置等的协变量起到至关重要的作用。【21】中将协变量结合到似然函数中,也可以通过定义数据之间基于协变量的距离来将其结合到先验中去。后面 这个方法的区别在于,它允许我们根据潜在特征来建模依赖关系。例如,两个在年龄上相仿或在地理位置上相近的人可能共享爱好兴趣,这个模式会被DDIBP很自然的表达。最后,在某些应用中建模团组数据之间共享的依赖结构是很有意义的。在脑图像的研究中,经常在subjects之间观测到相似的空间和时间的依赖性。【2,29】提及到,在分层模型中会强调在不影响subject内部变化性的同时建模共享结构。一种层次化扩展DDIBP的方法是允许衰减函数的参数根据不同的个体分组的不同而改变,而个体的分组是由更高层级变量来完成的。
Distance Dependent Infinite Latent Feature Model 阅读笔记1的更多相关文章
- [论文阅读笔记] node2vec Scalable Feature Learning for Networks
[论文阅读笔记] node2vec:Scalable Feature Learning for Networks 本文结构 解决问题 主要贡献 算法原理 参考文献 (1) 解决问题 由于DeepWal ...
- 论文阅读笔记(七)【TIP2018】:Video-Based Person Re-Identification by Simultaneously Learning Intra-Video and Inter-Video Distance Metrics
是由一篇 IJCAI2016 扩的期刊. 该篇会议论文的阅读笔记[传送门] 期刊扩充的部分:P-SI2DL 1.问题描述: 在会议论文中介绍的SI2DL方法采用了视频三元组作为视频关系(是否匹配)的逻 ...
- Distance dependent Chinese Restaurant Processes
Here is a note of Distance dependent Chinese Restaurant Processes 文章链接http://pan.baidu.com/s/1dEk7ZA ...
- 个性探测综述阅读笔记——Recent trends in deep learning based personality detection
目录 abstract 1. introduction 1.1 个性衡量方法 1.2 应用前景 1.3 伦理道德 2. Related works 3. Baseline methods 3.1 文本 ...
- Deep Learning of Graph Matching 阅读笔记
Deep Learning of Graph Matching 阅读笔记 CVPR2018的一篇文章,主要提出了一种利用深度神经网络实现端到端图匹配(Graph Matching)的方法. 该篇文章理 ...
- [阅读笔记]Software optimization resources
http://www.agner.org/optimize/#manuals 阅读笔记Optimizing software in C++ 7. The efficiency of differe ...
- Mongodb Manual阅读笔记:CH3 数据模型(Data Models)
3数据模型(Data Models) Mongodb Manual阅读笔记:CH2 Mongodb CRUD 操作Mongodb Manual阅读笔记:CH3 数据模型(Data Models)Mon ...
- javascript高级程序设计阅读笔记(一)
javascript高级程序设计阅读笔记(一) 工作之余开发些web应用作为兴趣,在交互方面需要掌握javascript和css.HTML5等技术,因此读书笔记是必要的. javascript简介 J ...
- Mysql DOC阅读笔记
Mysql DOC阅读笔记 转自我的Github Speed of SELECT Statements 合理利用索引 隔离调试查询中花费高的部分,例如函数调用是在结果集中的行执行还是全表中的行执行 最 ...
随机推荐
- DEVOPS技术实践_19:Pipeline的多参数json调用
在上一篇学习了把参数写进Json文件,然后通过去Json文件,调用参数的方法 1. 三元运算符介绍 调用的方法是通过一个三元运算符实现的 gender = prop.GENDER? prop.GEND ...
- DEVOPS技术实践_06:sonar与Jenksin集成
代码质量管理平台 一.checkout和打包功能 1.1 gitlab在新建一个文件 后续在写入内容 1.2 Jenkins新建一个任务 两个参数 1.3 流水线配置 copy仓库地址: http:/ ...
- 数据导出至excle
ASP.NET MVC导出Excel 首先下载 NPOI.dll 引用到项目中 建议下载地址:http://download.csdn.net/detail/pukuimin1226/5851747 ...
- iptables匹配端口范围,映射,网络状态
####匹配端口范围:iptables -I INPUT -p tcp -m multiport --dport 21,22,23,24 -j ACCEPT <==次选iptables -I I ...
- 【题解】Vijos1404 遭遇战(最短路图论套路)
[题解]Vijos1404 遭遇战(最短路图论套路) 感觉一定要有建模的思想,不管什么东西要抽象建模之后再用算法解决... 求最短代价就可能可以用最短路,这句话不是强行解释,而是因为图论建模过后,可能 ...
- JVM探秘:内存溢出
本系列笔记主要基于<深入理解Java虚拟机:JVM高级特性与最佳实践 第2版>,是这本书的读书笔记. 在 Java 虚拟机内存区域中,除了程序计数器外,其他几个内存区域都可能会发生OutO ...
- 高阶函数HOF和高阶组件HOC(Higher Order Func/Comp)
一.什么是高阶函数(组件),作用是什么? 子类使用父类的方法可以通过继承的方式实现,那无关联组件通信(redux).父类使用子类方法(反向继承)呢 为了解决类(函数)功能交叉/功能复用等问题,通过传入 ...
- js中的事件冒泡
事件冒泡和阻止事件冒泡: 事件冒泡的原理:从实际操作的元素(事件)向上级父元素一级一级执行下去,直到达到document/window,冒泡过程结束.例如:假设我有一个 div 盒子,里面嵌套了1个子 ...
- elk日志使用
elasticsearch +log4net.ElasticSearch+kibana(windows) 需要的东西(目前用的5.6版本) 1.先安装jdk和jre 配置java环境 2. ...
- JS 中检测数组的四种方法
今天和大家分享一下 JS 中检测是不是数组的四种方法,虽然篇幅不长,不过方法应该算是比较全面了. 1. instanceof 方法 instanceof 用于检测一个对象是不是某个类的实例,数组也是一 ...
