简单记录百度移动统计android无埋点sdk使用和monkey测试屏蔽通知栏的问题

1.无埋点sdk使用

很简单,下载完sdk后导入到项目中 , 参考sdk文档进行就可以了,个人觉得比友盟还简单,几行代码实现无埋点可视化圈选.

这里是文档地址 可视化圈选SDK接入

值得注意的是 从编译项目并启动运行开始，5分钟左右后即可在百度移动统计网站上看到对应的启动数据！

2.adb monkey测试屏蔽通知栏

Windows系统配置好adb环境后, 打开cmd窗口, 输入 adb shell monkey -p 应用包名 -v 点击次数 > ./DeskTop/log.txt

当monkey跑起来的时候,你会发现,通知栏被拉下来,网络被关闭或是其他导致不能对app进行正常测试的操作,很恶心.

去stackoverflow上找到一个有效的解决办法,现在分享给大家

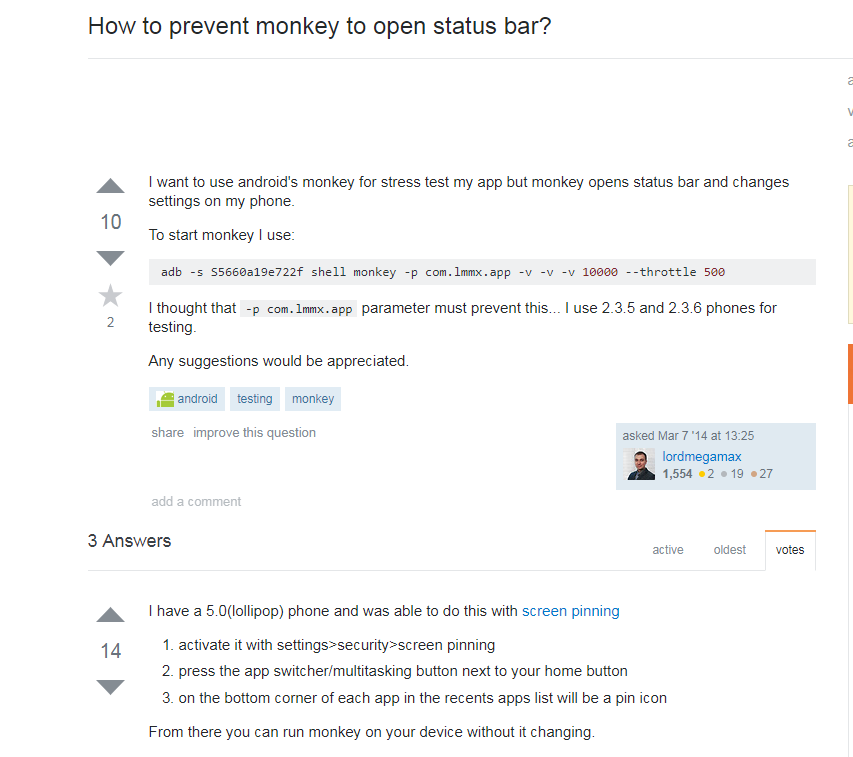
　　简单翻译一下:

第一步,去设置 - 安全和隐私 - 屏幕固定 , 开启屏幕固定. 具体方法可能因机型而异,荣耀V9的是这样的

　　　　

第二步,选中你的app的页面,固定屏幕.

第三步,cmd窗口运行monkey测试命令.测试结束的日志会写在桌面的log.txt里 


最后,贴个图看一下收获

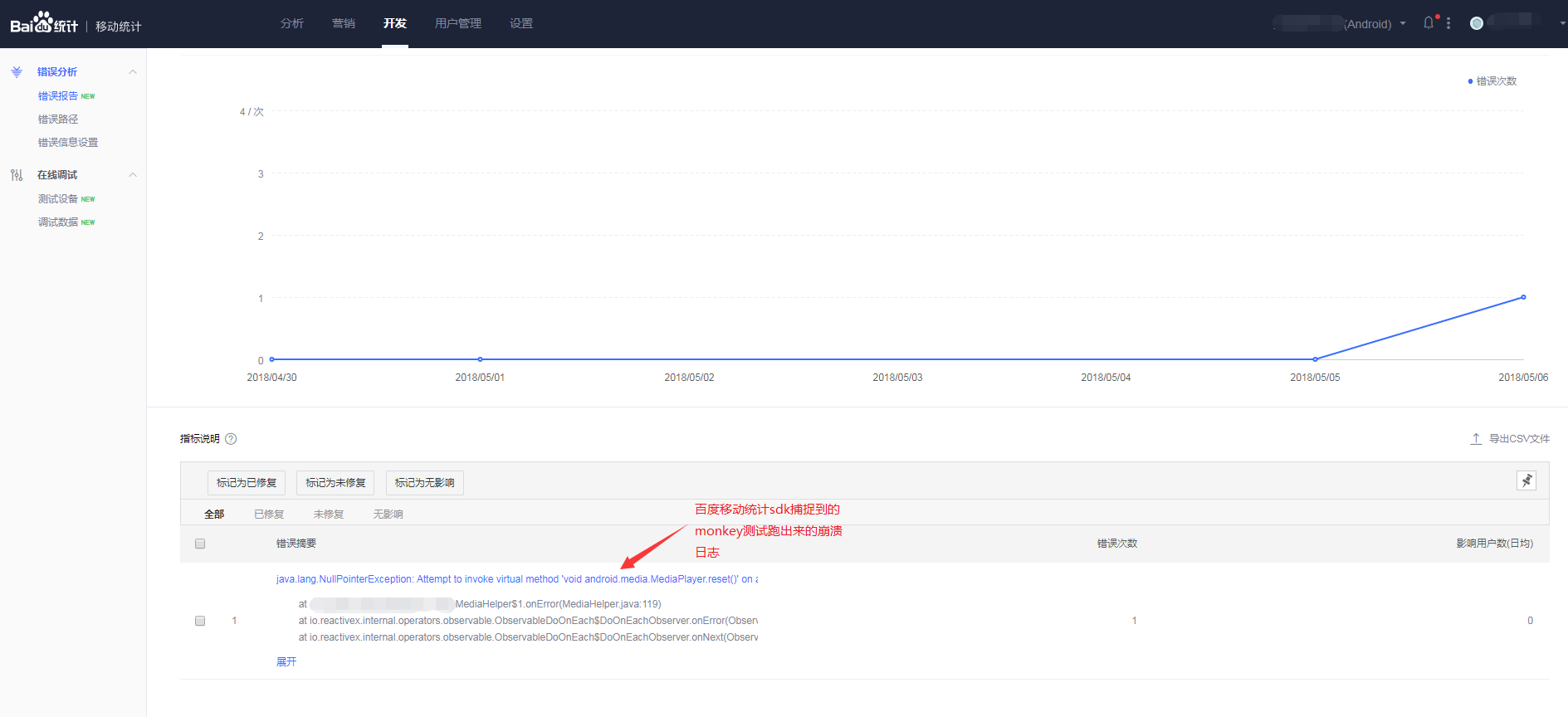
无埋点数据收集和adb monkey测试屏蔽通知栏的更多相关文章

  1. Android无埋点数据收集SDK关键技术

    前言 鉴于日益强烈的精细化运营需求,网易乐得从去年开始构建大数据平台,<<无埋点数据收集SDK>>因此立项,用于向大数据平台提供全量,完整,准确的客户端数据． << ...

  2. 埋点（Event Tracking）vs 无埋点（Codeless Tracking） vs 可视化埋点（Visual Event Tracking）

    在理解什么是埋点之前,首先需要了解一些基础知识:(以下摘自:http://www.chinawebanalytics.cn/auto-event-tracking-good-bad-ugly/) 我们 ...

  3. 揭开GrowingIO无埋点的神秘面纱

    揭开GrowingIO无埋点的神秘面纱   早在研究用户行为分析的时候,就发现国内的GrowingIO在宣传无埋点技术,最近正好抽出时间来研究一下所谓的无埋点到底是什么样的. 我分六部分来分析一下无埋 ...

  4. adb+monkey压力测试入门

    一.ADB安装步骤及ADB环境配置 1.ADB安装步骤 1)adb工具安装地址:http://www.wmzhe.com/soft-39913.html 2)下载安装包后,解压,将adb安装在根目录下 ...

  5. Appium -- adb monkey操作（一）

    1.Monkey简介在Android的官方自动化测试领域有一只非常著名的"猴子"叫Monkey,这只"猴子"一旦启动,就会让被测的Android应用程序像猴子一 ...

  6. adb Monkey用法

    以这条Monkey指令为例: #monkey -s --throttle -p com.android.cameraswitch -- 这条monkey指令是测试:在camera模块中产生1万次伪随机 ...

  7. adb monkey测试 命令

    adb shell monkey -p cn.com.linktrust.als.ipad 3500 LOWED_PACKAGE [-p ALLOWED_PACKAGE] ...] [-c MAIN_ ...

  8. App测试- adb monkey测试

    一. 安装和配置SDK 1. 下载Android SDK并解压.如下图:(如果不存在tool和platform_tool,请点击SDK Manager在线下载和更新) 2.下载完成后,配置SDK环境变 ...

  9. adb adb monkey命令及介绍

    1.adb的组成部分 守护进程,客户端,服务器端`      2.Monkey程序是Google公司提供的一个压力和稳定性测试的工具 3.命令 命令 参数 功能 adb version   查看当前a ...

随机推荐

  1. 转：深入了解Windows句柄

    深入了解Windows句柄到底是什么 转:http://blog.csdn.net/wenzhou1219/article/details/17659485 总是有新入门的Windows程序员问我Wi ...

  2. CSU 2151 集训难度【多标记线段树】

    http://acm.csu.edu.cn/csuoj/problemset/problem?pid=2151 Input 第一行三个数n,m,v0 表示有n名萌新和m次调整,初始时全部萌新的集训难度 ...

  3. 洛谷P1850换教室

    题目传送门 理解题意:给定你一个学期的课程和教室数量以及教室之间的距离还有换教室成功的概率,求一个学期走的距离的期望最小值 题目是有够恶心的,属于那种一看就让人不想刷的题目...很明显的动规,但是那个 ...

  4. 简单了解gzip、bzip2、xz

    压缩工具gzip.bzip2.xz分别对应压缩格式.gz..bz2..xz.不过tar命令已经可以满足大部分使用,所以这些格式只简单了解一下.gzip压缩速度最快,xz压缩率最高,bz2适中.一般这三 ...

  5. Flask实战第43天：把图片验证码和短信验证码保存到memcached中

    前面我们已经获取到图片验证码和短信验证码,但是我们还没有把它们保存起来.同样的,我们和之前的邮箱验证码一样,保存到memcached中 编辑commom.vews.py .. from utils i ...

  6. Java 对象池实现

    http://blog.csdn.net/bryantd/article/details/1100019 http://www.cnblogs.com/devinzhang/archive/2012/ ...

  7. luogu P2485 [SDOI2011]计算器

    题目描述 你被要求设计一个计算器完成以下三项任务: 1.给定y.z.p,计算y^z mod p 的值: 2.给定y.z.p,计算满足xy ≡z(mod p)的最小非负整数x: 3.给定y.z.p,计算 ...

  8. [BZOJ4709][JSOI2011]柠檬(斜率优化DP)

    显然选出的每一段首尾都是相同的,于是直接斜率优化,给每个颜色的数开一个单调栈即可. #include<cstdio> #include<vector> #include< ...

  9. 2017 Multi-University Training 2 解题报告

    Is Derek lying? Time Limit: 3000/1000 MS (Java/Others)    Memory Limit: 65536/65536 K (Java/Others)T ...

  10. 【DFS】Gym - 100781A - Adjoin the Networks

    给你一个森林,让你把它连接成一颗树,使得直径最小. 就求出每颗树的重心以后,全都往直径最大的那个的重心上连,一般情况是最大/2+次大/2+1,次大/2+第三大/2+2 中取较大者. 还有些特殊情况要特 ...