[bzoj1005][HNOI2008]明明的烦恼-Prufer编码+高精度

Brief Description

给出标号为1到N的点,以及某些点最终的度数,允许在

任意两点间连线,可产生多少棵度数满足要求的树?

Algorithm Design

结论题.

首先可以参考这篇文章了解一下什么是Prufer编码:

Cayley公式是说，一个完全图\(K_n\)有\(n^{n-2}\)棵生成树，换句话说n个节点的带标号的无根树有\(n^{n-2}\)个。今天我学到了Cayley公式的一个非常简单的证明，证明依赖于Prüfer编码，它是对带标号无根树的一种编码方式。

给定一棵带标号的无根树，找出编号最小的叶子节点，写下与它相邻的节点的编号，然后删掉这个叶子节点。反复执行这个操作直到只剩两个节点为止。由于节点数n>2的树总存在叶子节点，因此一棵n个节点的无根树唯一地对应了一个长度为n-2的数列，数列中的每个数都在1到n的范围内。下面我们只需要说明，任何一个长为n-2、取值范围在1到n之间的数列都唯一地对应了一棵n个节点的无根树，这样我们的带标号无根树就和Prüfer编码之间形成一一对应的关系，Cayley公式便不证自明了。

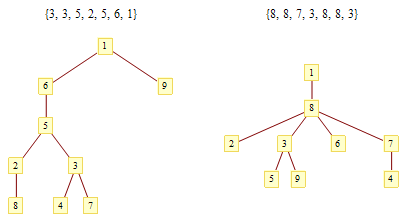
注意到，如果一个节点A不是叶子节点，那么它至少有两条边；但在上述过程结束后，整个图只剩下一条边，因此节点A的至少一个相邻节点被去掉过，节点A的编号将会在这棵树对应的Prüfer编码中出现。反过来，在Prüfer编码中出现过的数字显然不可能是这棵树（初始时）的叶子。于是我们看到，没有在Prüfer编码中出现过的数字恰好就是这棵树（初始时）的叶子节点。找出没有出现过的数字中最小的那一个（比如④），它就是与Prüfer编码中第一个数所标识的节点（比如③）相邻的叶子。接下来，我们递归地考虑后面n-3位编码（别忘了编码总长是n-2）：找出除④以外不在后n-3位编码中的最小的数（左图的例子中是⑦），将它连接到整个编码的第2个数所对应的节点上（例子中还是③）。再接下来，找出除④和⑦以外后n-4位编码中最小的不被包含的数，做同样的处理……依次把③⑧②⑤⑥与编码中第3、4、5、6、7位所表示的节点相连。最后，我们还有①和⑨没处理过，直接把它们俩连接起来就行了。由于没处理过的节点数总比剩下的编码长度大2，因此我们总能找到一个最小的没在剩余编码中出现的数，算法总能进行下去。这样，任何一个Prüfer编码都唯一地对应了一棵无根树，有多少个n-2位的Prüfer编码就有多少个带标号的无根树。

一个有趣的推广是，n个节点的度依次为D1, D2, …, Dn的无根树共有\(\frac{(n-2)!}{\prod{(D_i-1)!}}\)个，因为此时Prüfer编码中的数字i恰好出现Di-1次。

然后, 根据排列组合和计数原理的相关知识, 设没有限制的节点数为\(m\), 答案就是

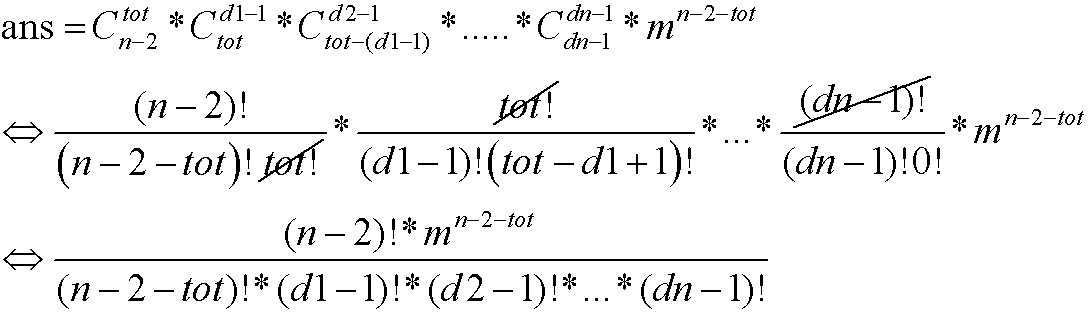
然后在分子和分母上分解因式, 把次数加加减减就好了.

Code

#include <algorithm>
#include <cctype>
#include <cstdio>
#include <cstring>
#define ll long long
const int maxn = 3000;
const ll mod = 1000000000000000;
inline int read() {
  int x = 0, f = 1;
  char ch = getchar();
  while (!isdigit(ch)) {
    if (ch == '-')
      f = -1;
    ch = getchar();
  }
  while (isdigit(ch)) {
    x = x * 10 + ch - '0';
    ch = getchar();
  }
  return x * f;
}
int n, m, tot, cnt;
ll d[maxn], num[maxn], prime[maxn], check[maxn], ans[maxn], l = 1;
void getprime() {
  for (int i = 2; i <= 1000; i++) {
    if (!check[i])
      prime[cnt++] = i;
    for (int j = 0; j < cnt; j++) {
      if (i * prime[j] > 1000)
        break;
      check[i * prime[j]] = 1;
      if (i % prime[j] == 0)
        break;
    }
  }
}
void solve(int a, int f) {
  for (int k = 1; k <= a; k++) {
    int x = k;
    for (int i = 0; i < cnt; i++) {
      if (x <= 1)
        break;
      while (x % prime[i] == 0) {
        num[i] += f;
        x /= prime[i];
      }
    }
  }
}
void mul(int x) {
  for (int i = 1; i <= l; i++)
    ans[i] *= x;
  for (int i = 1; i <= l; i++) {
    ans[i + 1] += ans[i] / mod;
    ans[i] %= mod;
  }
  while (ans[l + 1]) {
    l++;
    ans[l + 1] += ans[l] / mod;
    ans[l] %= mod;
  }
}
void print() {
  for (int i = l; i; i--)
    if (i == l)
      printf("%lld", ans[i]);
    else
      printf("%06lld", ans[i]);
}
int main() {
  getprime();
  ans[1] = 1;
  n = read();
  if (n == 1) {
    int x = read();
    if (!x || x == -1)
      printf("1");
    else
      printf("0");
    return 0;
  }
  for (int i = 1; i <= n; i++) {
    d[i] = read();
    if (!d[i]) {
      printf("0");
      return 0;
    }
    if (d[i] == -1)
      m++;
    else {
      d[i]--;
      tot += d[i];
    }
  }
  if (tot > n - 2) {
    printf("0");
    return 0;
  }
  solve(n - 2, 1);
  solve(n - 2 - tot, -1);
  for (int i = 1; i <= n; i++)
    solve(d[i], -1);
  for (int i = 0; i < cnt; i++)
    while (num[i]--)
      mul(prime[i]);
  for (int i = 1; i <= n - 2 - tot; i++)
    mul(m);
  print();
  return 0;
}