Sklearn线性回归
Sklearn线性回归
原理
线性回归是最为简单而经典的回归模型,用了最小二乘法的思想,用一个n-1维的超平面拟合n维数据
数学形式
\]
其中称\(w=(w_1,w_2,w_3,...w_n)\)为系数矩阵(coef_),称\(w_0\)为截距(intercept_)
基本步骤
- 准备数据集
- 使用线性回归
- 训练模型
- 使用训练后的模型预测
- 模型评估
下面以二维数据举例
例子
#coding=utf-8
import pandas as pd
from sklearn import linear_model
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
def main():
#数据预处理
ad = pd.read_csv('./Advertising.csv',index_col=0)
#为了方便,只取一列作为研究
X = ad[['TV']] #注意此时X的数据类型是dataFrame,如果只有一个括号,类型为Series会报错
Y = ad[['Sales']]
#这里采用交叉验证法划分数据集
X_train, X_test, Y_train, Y_test =train_test_split(X, Y)
#创建回归模型对象
lr = linear_model.LinearRegression()
lr.fit(X_train.values.reshape(-1, 1), Y_train.values.reshape(-1, 1))
#显示训练结果
print lr.intercept_,lr.coef_
print lr.score(X_test, Y_test) #用R^2评估
plt.plot(X,lr.predict(X))
plt.scatter(X,Y)
plt.show()
if __name__ == '__main__':
main()
'''
输出结果
[ 7.21071682] [[ 0.0460963]]
0.713025893451
'''
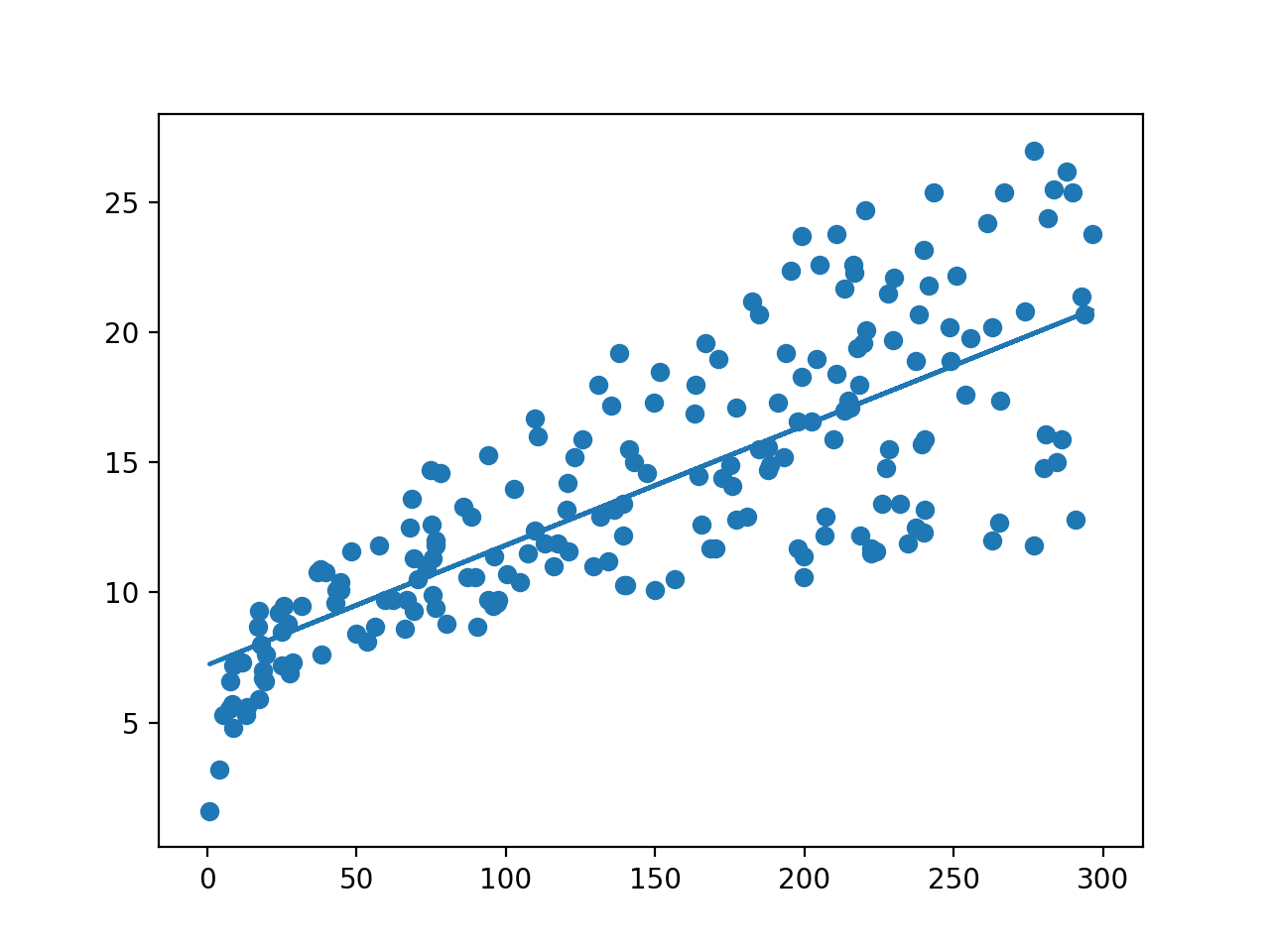
关于模型评估
这里采用的是\(R^2\)拟合优度检验,是一个属于0~1的值,\(R^2\)越大表示拟合程度越好
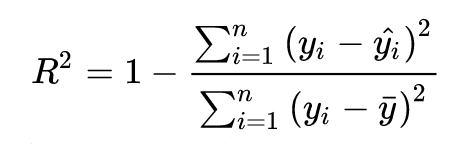
Sklearn线性回归的更多相关文章
- sklearn线性回归实现房价预测模型
目录 题目要求 单特征线性回归 方案一 方案二 多特征线性回归 两份数据 ex1data1.txt ex1data2.txt 题目要求 建立房价预测模型:利用ex1data1.txt(单特征)和ex1 ...
- sklearn 线性回归
# import numpy as np import pandas as pd from pandas import Series,DataFrame import matplotlib.pyplo ...
- 『科学计算』通过代码理解线性回归&Logistic回归模型
sklearn线性回归模型 import numpy as np import matplotlib.pyplot as plt from sklearn import linear_model de ...
- Scikit-Learn 机器学习笔记 -- 线性回归、逻辑回归、softma
import numpy as np from matplotlib import pyplot as plt # 创建线性回归数据集 def create_dataset(): X = 2 * ...
- skearn自学路径
sklearn学习总结(超全面) 关于sklearn,监督学习几种模型的对比 sklearn之样本生成make_classification,make_circles和make_moons pytho ...
- Sklearn库例子2:分类——线性回归分类(Line Regression )例子
线性回归:通过拟合线性模型的回归系数W =(w_1,…,w_p)来减少数据中观察到的结果和实际结果之间的残差平方和,并通过线性逼近进行预测. 从数学上讲,它解决了下面这个形式的问题: Lin ...
- sklearn库 线性回归库 LinearRegression
import numpy as np import sklearn.datasets #加载原数据 from sklearn.model_selection import train_test_spl ...
- 使用sklearn机器学习库实现线性回归
import numpy as np # 导入科学技术框架import matplotlib.pyplot as plt # 导入画图工具from sklearn.linear_model imp ...
- sklearn学习笔记之简单线性回归
简单线性回归 线性回归是数据挖掘中的基础算法之一,从某种意义上来说,在学习函数的时候已经开始接触线性回归了,只不过那时候并没有涉及到误差项.线性回归的思想其实就是解一组方程,得到回归函数,不过在出现误 ...
随机推荐
- C#算法 选择排序、冒泡排序、插入排序
1.冒泡排序: 方法一: public static int[] MaoPao(int[] arr) { //执行多少次 for (int i = 0; i < arr.Length; i++) ...
- idea格式化代码无效Ctrl+Alt+L
1.Idea格式化代码,无效,我的原因是热键冲突,我按Ctrl+Alt+L的时候,竟然弹出了锁QQ,果断关了QQ的热键,百度有的是网易啥的,具体情况具体分析吧.
- Linux(CentOS7)安装Tomcat
概述 Tomcat是运行Jsp文件的容器服务,能够处理URL请求,类似于IIS.相对于IIS,Tomcat可以部署到Linux.Windows.IOS等操作系统.这里主要整理将Tomcat部署到Lin ...
- scrapy笔记
1.关于请求url状态码重定向问题: from scrapy import Request handle_httpstatus_list = [404, 403, 500, 503, 521, 522 ...
- lvs-ldirectord
Ldirectord;用来对后端服务器的检测状态后并进行操作 安装在director上 对后端的rs服务器的 健康检查包括几方面: 1通过ping 若可以ping到服务器表示主机活着 2 对端口的检 ...
- k8s教程
k8s教程地址 安装https://github.com/gjmzj/kubeaszhttps://github.com/opsnull/follow-me-install-kubernetes-cl ...
- Vue2.0学习——axios用法详解
功能特性 在浏览器中发送 XMLHttpRequests 请求 在 node.js 中发送 http请求 支持 Promise API 拦截请求和响应 转换请求和响应数据 自动转换 JSON 数据 客 ...
- Codeforces 1017F The Neutral Zone 数论
原文链接https://www.cnblogs.com/zhouzhendong/p/CF1017F.html 题目传送门 - CF1017F 题意 假设一个数 $x$ 分解质因数后得到结果 $x=p ...
- day 35 协程与gil概念
博客链接: http://www.cnblogs.com/linhaifeng/articles/7429894.html 今日概要: 1 生产者消费者模型(补充) 2 GIL(进程与线程的应用场景) ...
- JavaEE 之 DBCP
1.DBCP a.定义:DBCP(DataBase Connection Pool)数据库连接池,是java数据库连接池的一种,由Apache开发,通过数据库连接池,可以让程序自动管理数据库连接的释放 ...
