002-红黑树【B-树】、二叉查找树

一、引述-二叉查找树

　　红黑树（Red Black Tree） 一种特殊的二叉查找树。故先查看二叉查找树

　　二叉查找树特性：左字数上所有的节点的值都小于或等于他的根节点上的值

右子树上所有节点的值均大于或等于他的根节点的值

左、右子树也跟别为平衡二叉树

1.1、示例

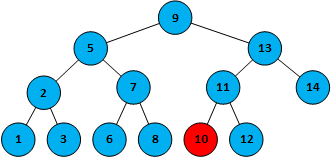
一个基本的二叉查找树

　　

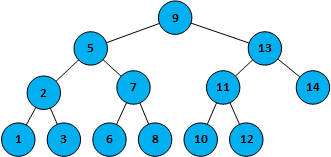
需求查找数据10，

第一步,查看根节点9，命中节点9

　　

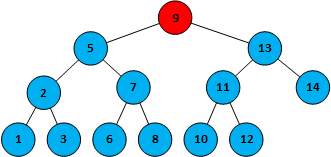
第二步，10>9，在根节点9的右侧，命中13

　　

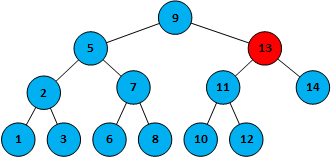
第三步，13>10，在节点13的左侧，命中11

　　

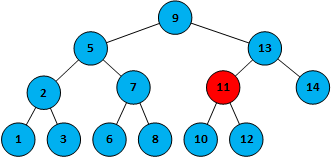
第四部，11>10,在节点11的左侧，命中10

　　

不过二叉查找树有一些问题，可能会出现不平横的情况，即如下图所示的情况

　　

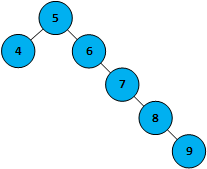
从这种情况可以看出，明显存在左子树和右子树深度相差过多，在使用平衡情况下的二叉查找树是时间复杂度为logn，而出现这种极端情况的话，想要查9的位置就需要每一次都遍历下一个右子树，很有可能时间复杂度变为n(与数组普通查询的时间复杂度相同)

基于上述情况，引入了平衡二叉树，红黑树即为平衡二叉树的一种

二、红黑树概述

　　红黑树（Red Black Tree） 是一种自平衡二叉查找树。别名：对称二叉B树、

　　红黑树和AVL树类似，都是在进行插入和删除操作时通过特定操作保持二叉查找树的平衡，从而获得较高的查找性能。

　　它虽然是复杂的，但它的最坏情况运行时间也是非常良好的，并且在实践中是高效的： 它可以在O(log n)时间内做查找，插入和删除，这里的n 是树中元素的数目。

2.1、数据结构

　　它的统计性能要好于平衡二叉树(有些书籍根据作者姓名，Adelson-Velskii和Landis，将其称为AVL-树)，因此，红黑树在很多地方都有应用。在C++ STL中，很多部分(包括set, multiset, map, multimap)应用了红黑树的变体(SGI STL中的红黑树有一些变化，这些修改提供了更好的性能，以及对set操作的支持)。其他平衡树还有：AVL，SBT，伸展树，TREAP 等等。

2.2、树的性质

　　红黑树是每个节点都带有颜色属性的二叉查找树，颜色或红色或黑色。在二叉查找树强制一般要求以外，对于任何有效的红黑树我们增加了如下的额外要求:

　　　　性质1. 节点是红色或黑色。

　　　　性质2. 根节点是黑色。

　　　　性质3 每个叶节点（NIL节点，空节点）是黑色的。

　　　　性质4 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)

　　　　性质5. 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。

 

　　这些约束强制了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。结果是这个树大致上是平衡的。因为操作比如插入、删除和查找某个值的最坏情况时间都要求与树的高度成比例，这个在高度上的理论上限允许红黑树在最坏情况下都是高效的，而不同于普通的二叉查找树。

　　要知道为什么这些特性确保了这个结果，注意到性质4导致了路径不能有两个毗连的红色节点就足够了。最短的可能路径都是黑色节点，最长的可能路径有交替的红色和黑色节点。因为根据性质5所有最长的路径都有相同数目的黑色节点，这就表明了没有路径能多于任何其他路径的两倍长。

　　 正是由于这些原因使得红黑树是一个平衡二叉树

2.3、树的旋转　　

　　当我们在对红黑树进行插入和删除等操作时，对树做了修改，那么可能会违背红黑树的性质。

　　为了保持红黑树的性质，我们可以通过对树进行旋转，即修改树中某些结点的颜色及指针结构，以达到对红黑树进行插入、删除结点等操作时，红黑树依然能保持它特有的性质（五点性质）。

　　当查找树的结构发生改变时，红黑树的条件可能被破坏，需要通过调整使得查找树重新满足红黑树的条件。调整可以分为两类：一类是颜色调整，即改变某个节点的颜色；另一类是结构调整，集改变检索树的结构关系。结构调整过程包含两个基本操作：左旋（Rotate Left），右旋（RotateRight）。

2.3.1、左旋

左旋的过程是将x的右子树绕x逆时针旋转，使得x的右子树成为x的父亲，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

　　

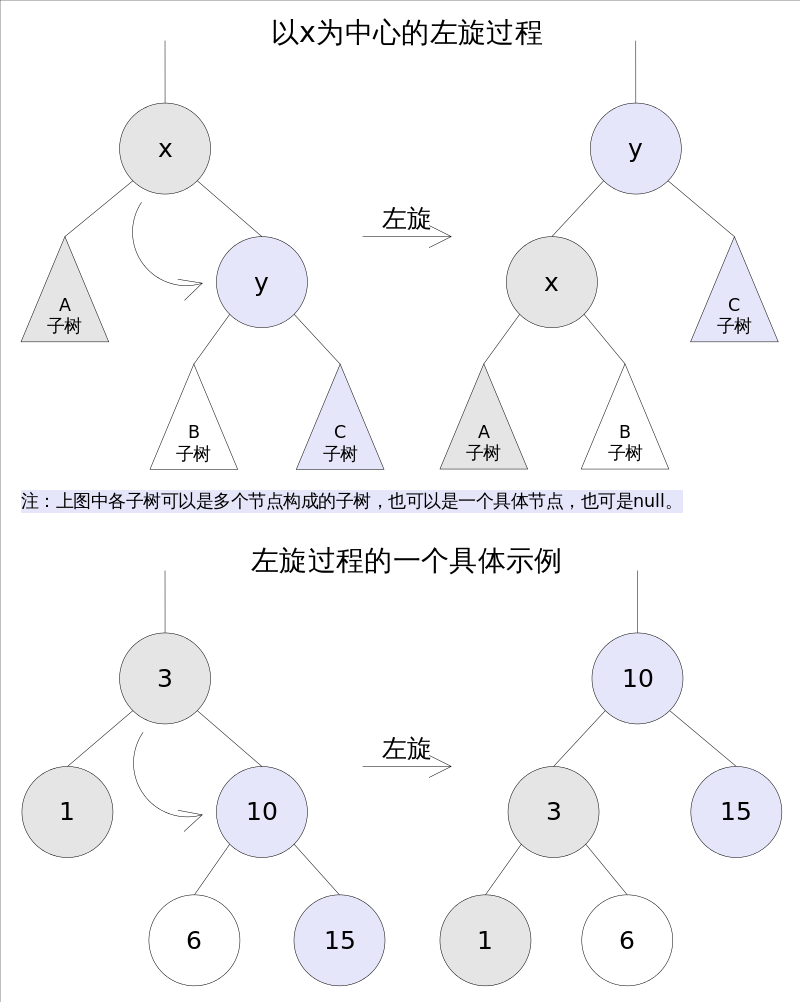
2.3.2、右旋

右旋的过程是将x的左子树绕x顺时针旋转，使得x的左子树成为x的父亲，同时修改相关节点的引用。旋转之后，二叉查找树的属性仍然满足。

　　

2.3.3、小结

无论是左旋还是右旋，被旋转的树，在旋转前是二叉查找树，并且旋转之后仍然是一颗二叉查找树。

　　

2.4、示例

1、基础示例

　　

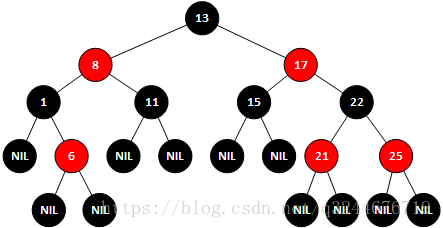
示例一、向红黑树中插入节点14(一般默认插入节点是红色的)

　　

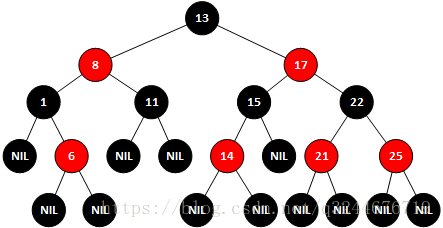
示例二、在原树上插入20

　　

　　可以看到，插入以后树已经不是一个平衡的二叉树，而且并不满足红黑树的要求，因为20和21均为红色，这种情况下就需要对红黑树进行变色，21需要变为黑色，22就会变成红色，如果22变成红色，则需要17和25都变成黑色

　　

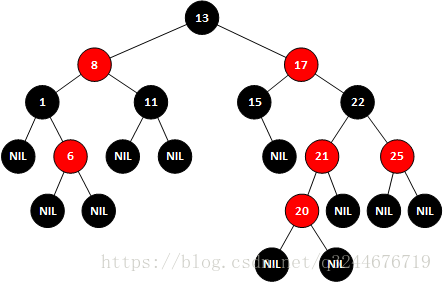
　　而17变成黑色显然是不成立的，因为如果17变为黑色，那么13就会变为红色，不满足二叉树的规则，因此此处需要进行另一个操作---------左旋操作

以节点17进行左旋操作

　　对于上图由于右子树中17变为黑色以后需要把13变成红色，因此进行一次左旋，将17放在根节点，这样既可保证13为红色，左旋后结果

　　　　

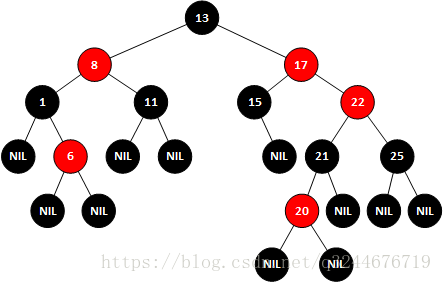
　　 而后根据红黑树的要求进行颜色的修改

　　　　

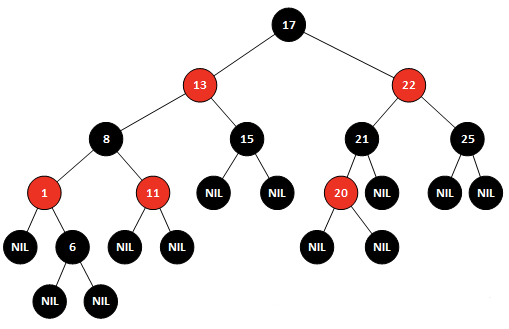
　　进行左旋后，发现从根节点17，到1左子树的叶子节点经过了两个黑节点，而到6的左叶子节点或者右叶子节点要经历3个黑节点，很显然也不满足红黑树，因此还需要进行下一步操作，需要进行右旋操作

以节点13进行右旋

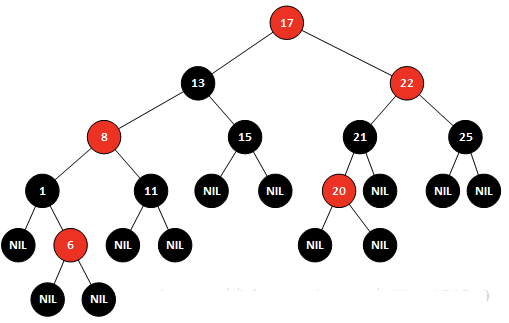
　　由于是从13节点出现的不平衡，因此对13节点进行右旋，得到结果

　　　　

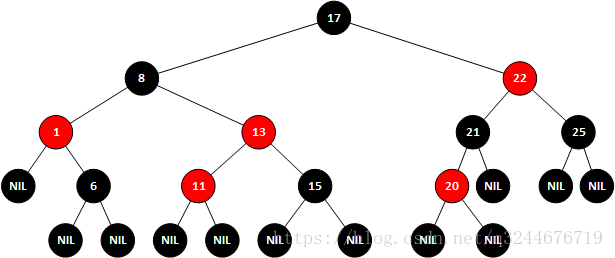
　　而后再对其节点进行变色，得到结

　　　　

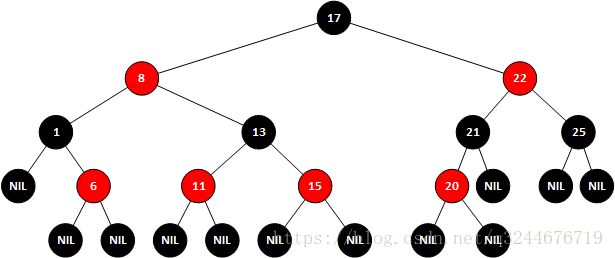
　　这便是红黑树的一个变换，它主要用途有很多，例如java中的TreeMap以及JDK1.8以后的HashMap在当个节点中链表长度大于8时都会用到。

参看地址：

　　https://www.cnblogs.com/CarpenterLee/p/5503882.html