prim算法java版

public class Prim {

    static int MAX = 65535;
    public static void prim(int[][] graph, int n){

        char[] c = new char[]{'A','B','C','D','E','F','G','E','F'};
        int[] lowcost = new int[n];
        int[] mst = new int[n];
        int i, j, min, minid, sum = 0;

        for(i = 1; i < n; i++){
            lowcost[i] = graph[0][i];
            mst[i] = 0;
        }

        for(i = 1; i < n; i++){

            min = MAX;
            minid = 0;
            for(j = 1; j < n; j++){
                if (lowcost[j] < min && lowcost[j] != 0) {
                    min = lowcost[j];
                    minid = j;
                }
            }
            System.out.println(c[mst[minid]] + "到" + c[minid] + " 权值：" + min);

            sum += min;
            lowcost[minid] = 0;

            for (j = 1; j < n; j++) {
                if (graph[minid][j] < lowcost[j]) {
                    lowcost[j] = graph[minid][j];
                    mst[j] = minid;
                }
            }
        }

        System.out.println("sum:" + sum);

    }

    public static void main(String[] args) {
                int[][] map = new int[][]{
                {0,10,MAX,MAX,MAX,11,MAX,MAX,MAX},
                {10,0,18,MAX,MAX,MAX,16,MAX,12},
                {MAX,MAX,0,22,MAX,MAX,MAX,MAX,8},
                {MAX,MAX,22,0,20,MAX,MAX,16,21},
                {MAX,MAX,MAX,20,0,26,MAX,7,MAX},
                {11,MAX,MAX,MAX,26,0,17,MAX,MAX},
                {MAX,16,MAX,MAX,MAX,17,0,19,MAX},
                {MAX,MAX,MAX,16,7,MAX,19,0,MAX},
                {MAX,12,8,21,MAX,MAX,MAX,MAX,0}
        };
        prim(map, map.length);
    }

}

输出结果：

A到B 权值：
A到F 权值：
B到F 权值：
F到C 权值：
B到G 权值：
G到E 权值：
E到E 权值：
E到D 权值：
sum:

 

prim算法的思想：

• 初始化时，v0加入到最小树，其他所有顶点作为未加入树的集合
• 取矩阵中第一横，lowcost[]，其实就是v0与其他顶点的距离，找出最小的，比如v4，v4加入到最小树，此时最小数有两个节点了v0和v4
• 接下来，要找到其他未加入树顶点中与最小树顶点距离最近的那个点
• • lowcost[]这是v0的数据
  • 找到v4与其他顶点的距离数据，即矩阵的第5横 tmp[]
  • 然后rmp[]和lowcost[]纵向对比大小，小的数据设置到lowcost[]
  • 然后横向对比lowcost[]数据，找到最小点X，这个X即为与最小树距离最近的那个点
• 同理，依次将所有顶点加入到最小树

WIKI解释

图例	说明	不可选	可选	已选
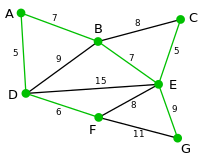
	此为原始的加权连通图。每条边一侧的数字代表其权值。	-	-	-
	顶点D被任意选为起始点。顶点A、B、E和F通过单条边与D相连。A是距离D最近的顶点，因此将A及对应边AD以高亮表示。	C, G	A, B, E, F	D
	下一个顶点为距离D或A最近的顶点。B距D为9，距A为7，E为15，F为6。因此，F距D或A最近，因此将顶点F与相应边DF以高亮表示。	C, G	B, E, F	A, D
	算法继续重复上面的步骤。距离A为7的顶点B被高亮表示。	C	B, E, G	A, D, F
	在当前情况下，可以在C、E与G间进行选择。C距B为8，E距B为7，G距F为11。E最近，因此将顶点E与相应边BE高亮表示。	无	C, E, G	A, D, F, B
	这里，可供选择的顶点只有C和G。C距E为5，G距E为9，故选取C，并与边EC一同高亮表示。	无	C, G	A, D, F, B, E
	顶点G是唯一剩下的顶点，它距F为11，距E为9，E最近，故高亮表示G及相应边EG。	无	G	A, D, F, B, E, C