HD 1533 Going Home（最小费用最大流模板）

Going Home

Time Limit: 10000/5000 MS (Java/Others)    Memory Limit: 65536/32768 K (Java/Others)
Total Submission(s): 3666    Accepted Submission(s):
1884

Problem Description

On a grid map there are n little men and n houses. In
each unit time, every little man can move one unit step, either horizontally, or
vertically, to an adjacent point. For each little man, you need to pay a $1
travel fee for every step he moves, until he enters a house. The task is
complicated with the restriction that each house can accommodate only one little
man.

Your task is to compute the minimum amount of money you need to pay
in order to send these n little men into those n different houses. The input is
a map of the scenario, a '.' means an empty space, an 'H' represents a house on
that point, and am 'm' indicates there is a little man on that point.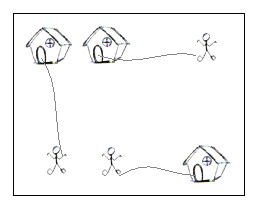

You can think of each
point on the grid map as a quite large square, so it can hold n little men at
the same time; also, it is okay if a little man steps on a grid with a house
without entering that house.

 

Input

There are one or more test cases in the input. Each
case starts with a line giving two integers N and M, where N is the number of
rows of the map, and M is the number of columns. The rest of the input will be N
lines describing the map. You may assume both N and M are between 2 and 100,
inclusive. There will be the same number of 'H's and 'm's on the map; and there
will be at most 100 houses. Input will terminate with 0 0 for N and M.

 

Output

For each test case, output one line with the single
integer, which is the minimum amount, in dollars, you need to pay.

 

Sample Input

2 2
.m
H.
5 5
HH..m
.....
.....
.....
mm..H
7 8
...H....
...H....
...H....
mmmHmmmm
...H....
...H....
...H....
0 0

 

Sample Output

2
10
28

 

Source

Pacific
Northwest 2004

题意：

...H....

...H....

...H....

mmmHmmmm

...H....

...H....

...H....

问所有H移动到所有m上花费最少的步数

以所有H 到 所有m 连一条边，边的权重为两者者距离，然后加一个超级源点和汇点，与原点的流量为1，费用为0，汇点也是一样。

转换成了求嘴小费用最大流问题；

//刘汝佳模板
#include <iostream>
#include <cstring>
#include <algorithm>
#include <cstdio>
#include <vector>
#include <cmath>
#include <queue>
using namespace std;
const int MAXN = 400;
const int MAXM = 200000;
const int INF = 0x3f3f3f3f;
struct Edge
{
    int from,to,cap,cost,flow;
    Edge(int u,int v,int c,int f,int w):from(u),to(v),cap(c),cost(f),flow(w){}
};
vector<Edge> edge;
vector<int> g[MAXN];
int inq[MAXN],d[MAXN],p[MAXN],a[MAXN];
int NN,MM;
int topH,topP;
struct point
{
    int x,y;
}H[MAXN],P[MAXN];

void input()
{
    char ch;
    topH = topP = 0;
    for(int i = 1; i <= NN; i++)
    {
        for(int j = 1; j <= MM; j++)
        {
            scanf("%c",&ch);
            if(ch == 'H')
            {
                topH++;
                H[topH].x = i;
                H[topH].y = j;
            }
            else if(ch == 'm')
            {
                topP++;
                P[topP].x = i;
                P[topP].y = j;
            }
        }
        getchar();
    }
}
void AddEdge(int from, int to, int cap, int cost)
{
    edge.push_back(Edge(from,to,cap,cost,0));
    edge.push_back(Edge(to,from,0,-cost,0));
    int m = edge.size();
    g[from].push_back(m - 2);
    g[to].push_back(m - 1);
}
int MCMF(int s,int t,int& flow, int& cost)
{

    for(int i = 0; i < MAXN; i++)
        d[i] = INF;
    memset(inq, 0, sizeof(inq));
    d[s] = 0;
    inq[s] = 1;
    p[s] = 0;
    a[s] = INF;

    queue<int> myque;
    myque.push(s);
    while(myque.empty() == 0)
    {
        int u = myque.front();
        myque.pop();
        inq[u] = 0;
        for(int i = 0; i < (int)g[u].size(); i++)
        {
            Edge e = edge[ g[u][i] ];
            if(e.cap > e.flow && d[e.to] > d[u] + e.cost)
            {
                d[e.to] = d[u] + e.cost;
                p[e.to] = g[u][i];
                a[e.to] = min(a[u], e.cap - e.flow);
                if(inq[e.to] == 0)
                {
                    myque.push(e.to);
                    inq[e.to] = 1;
                }
            }
        }
    }
    if(d[t] == INF)
        return false;
    flow += a[t];
    cost += d[t] * a[t];

    for(int u = t; u != s; u = edge[ p[u] ].from)
    {
        edge[ p[u] ].flow += a[t];
        edge[ p[u] ^ 1].flow -= a[t];
    }
    return true;

}
int creatGraph()
{
    int ans = 0,flow = 0;
    int MN = topH + topP;
    for(int i = 1; i <= topP; i++)
    {
        for(int j = 1; j <= topH; j++)
        {
            int t = abs(H[i].x - P[j].x) + abs(H[i].y - P[j].y);  //距离最为费用
            AddEdge(i,topP + j, 1, t);   // 边i到topP+j，把所有H.m点都排号序号
        }
    }

    for(int i = 1; i <= topP; i++)
        AddEdge(MN + 1, i, 1, 0);     //源点到M点
    for(int i = topP + 1; i <= MN; i++)
        AddEdge(i, MN + 2, 1,0);     // H点到汇点
    while(MCMF(MN + 1, MN + 2, flow, ans) );
    return ans;
}
int main()
{
    while(scanf("%d%d",&NN,&MM) != EOF)
    {
        if(NN == 0 && MM == 0)
            break;
        getchar();
        for(int i = 1; i < MAXN; i++)
            g[i].clear();
        edge.clear();
        input();
        printf("%d\n",creatGraph());
    }
    return 0;
}