最短路径之迪杰斯特拉（Dijkstra）算法

迪杰斯特拉（Dijkstra）算法主要是针对没有负值的有向图，求解其中的单一起点到其他顶点的最短路径算法。本文主要总结迪杰斯特拉（Dijkstra）算法的原理和算法流程，最后通过程序实现在一个带权值的有向图中，选定某一个起点，求解到达其它节点的最短路径，来加深对算法的理解。

1 算法原理

迪杰斯特拉（Dijkstra）算法是一个按照路径长度递增的次序产生的最短路径算法。下图为带权值的有向图，作为程序中的实验数据。

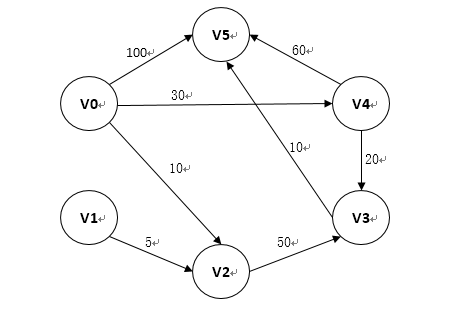
其中，带权值的有向图采用邻接矩阵graph来进行存储，在计算中就是采用n*n的二维数组来进行存储，v0-v5表示数组的索引编号0-5，二维数组的值表示节点之间的权值，若两个节点不能通行，比如，v0->v1不能通行，那么$graph[0,1]=\infty$ （采用计算机中最大正整数来进行表示）。那如何求解从v0每个v节点的最短路径长度呢?



首先，引进一个辅助数组cost，它的每个值$cost[i]$表示当前所找到的从起始点v0到终点vi的最短路径的权值（长度花费），该数组的初态为：若从v0到vi有弧，则$cost[i]$为弧上的权值，否则置$cost[i]$为$\infty$ 。显然，长度为：

$$

cost[j]=Min_i(graph[0,i] | v_i \in V)

$$

的路径就是从v0出发的长度最短的一条最短路径。此路径为$(v_0,v_j)$ ，那么下次长度次短的路径必定是弧$(v_0,v_i)$ 上的权值$cost[i](v_i \in V)$，或者是$cost[k](v_k \in S)$ 和弧$(v_k,v_i)$ 的权值之和。其中V：待求解最短路径的节点j集合；S：已求解最短路径的节点集合。

其实迪杰斯特拉（Dijkstra）最短路径算法是上一篇文迷宫问题求解之“A*搜索”（二）所讲到的 A*搜索算法中的一个特例，当A *搜索算法中 h(n)函数为0的时候，那么它就是迪杰斯特拉算法，算法原理一样，只不过在写程序的时候稍微有点区别而已。

2 算法流程

根据上面的算法原理分析，下面描述算法的实现流程。

1. 初始化：初始化辅助数组cost，从v0出发到图上其余节点v的初始权值为：$cost[i]=graph[0,i] \ |\ v_i \in V$ ；初始化待求节点S集合，它的初始状态为空集。

2. 选择节点$v_j$ ，使得$cost[j]=Min ( cost[i] | v_i \in V -S )$ ，$v_j$ 就是当前求的一条从v0出发的最短路径的终点，修改S集合，使得$S=S\bigcup V_j$ 。

3. 修改从v0出发到节点V-S上任一顶点$v_k$ 可达的最短路径，若cost[j]+graph[j,k]<cost[k] ，则修改cost[k]为：cost[k]=cost[j]+graph[j,k] 。

4. 重复操作2，3步骤，直到求解集合V中的所有节点为止。

其中最短路径的存储采用一个path整数数组，path[i]的值记录vi的前一个节点的索引，通过path一直追溯到起点，就可以找到从vi到起始节点的最短路径。比如起始节点索引为0，若path[3]=4, path[4]=0；那么节点v2的最短路径为，v0->v4->v3。

3 算法实现

采用c#语言对第2节中的算法流程进行实现，关键代码如下。

3.1 最短路径代码

class DijkstraSolution
{
    /*
        * 求解各节点最短路径，获取path，和cost数组，
        * path[i]表示vi节点的前继节点索引，一直追溯到起点。
        * cost[i]表示vi节点的花费
        */
    public static void FindShortestPath(int[,] graph,int startIndex, int[] path, int[] cost,int max)
    {
        int nodeCount = graph.GetLength(0);
        bool[] v = new bool[nodeCount];
        //初始化 path，cost，V
        for (int i = 0; i <nodeCount ; i++)
        {
            if (i == startIndex)//如果是出发点
            {
                v[i] = true;//
            }
            else
            {
                cost[i] = graph[startIndex,i ];
                if (cost[i] < max) path[i] = startIndex;
                else path[i] = -1;
                v[i] = false;
            }
        }
        //
        for(int i=1;i<nodeCount;i++)//求解nodeCount-1个
        {
            int minCost = max ;
            int curNode=-1;
            for (int w = 0; w < nodeCount; w++)
            {
                if (!v[w])//未在V集合中
                {
                    if(cost[w]<minCost)
                    {
                        minCost = cost[w];
                        curNode = w;
                    }
                }
            }//for  获取最小权值的节点
            if (curNode == -1) break;//剩下都是不可通行的节点，跳出循环
            v[curNode] = true;
            for (int w = 0; w < nodeCount; w++)
            {
                if (!v[w] && (graph[curNode, w] + cost[curNode] < cost[w]))
                {
                    cost[w] = graph[curNode, w] + cost[curNode];//更新权值
                    path[w] = curNode;//更新路径
                }
            }//for 更新其他节点的权值（距离）和路径
        }//
    }
}

3.2 调用代码

int max = 10000;
int[,] graph = new int[6, 6] {
    {max,max,10,max,30,100},
    {max,max,5,max,max,max},
    {max,max,max,50,max,max},
    {max,max,max,max,max,10},
    {max,max,max,20,max,60},
    {max,max,max,max,max,max},
};
int []path = new int[6];
int []cost = new int[6];
DijkstraSolution.FindShortestPath(graph, 0, path, cost,max);

3.3 运行结果

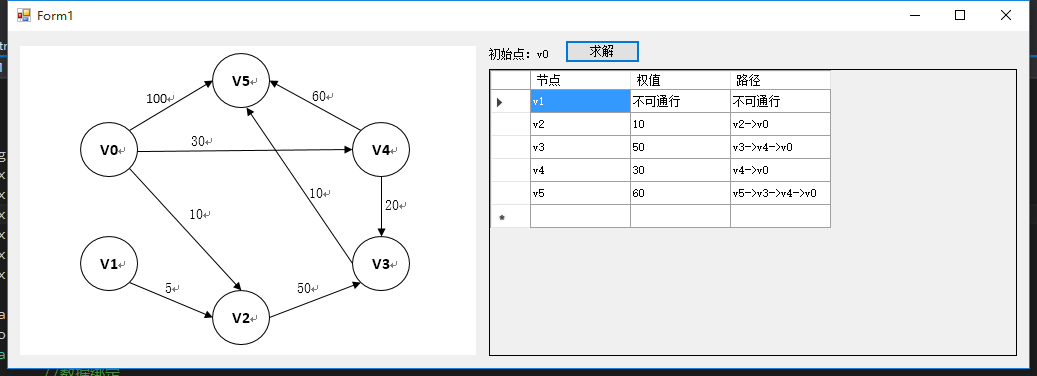
4 总结

迪杰特拉斯算法求解了一个起始节点到所有其他节点的最短路径，时间复杂度为$O(n^2)$ ，即使人们可能只想知道从起始节点到某个特定的节点的最短路径，时间复杂度同样为$O(n^2)$ 。

理解一个算法和实现一个算法还有有些区别的。理解一个算法，只需要明白算法原理和它的逻辑过程即可，但是实现一个算法，不仅要明白算法的逻辑过程，还考究我们的程序设计能力。

5 参考资料和资源

参考资料：严蔚敏的《数据结构c语言版》

源代码：http://download.csdn.net/download/mingge38/9657216