二叉查找树的实现与讲解(C++)

注：这篇文章源于：https://mp.csdn.net/postedit/99710904， 无需怀疑抄袭，同一个作者，这是我在博客园的账号。

在二叉树中，有两种非常重要的条件，分别是两类数据结构的基础性质。 其一是“堆性质”，二叉堆以及高级数据结构中的所有可合并堆都满足“堆 性质”。 其二是 “BST性质”，它是二叉查找树（Binary Search Tree）以及所有平衡树的基础。

二叉查找树的定义

   给定一棵二叉树，树上的每个节点都带有一个数值，成为节点的 “关键码” 。所谓BST性质是指，对于树中的任意一个节点：

·该节点的关键码不小于它的左子树（如果非空）中任意节点的关键码

·该节点的关键码不大于它的右子树（如果非空）中任意节点的关键码 满足上述性质的二叉树就是一棵“二叉查找树”（BST）。 二叉查找树的中序遍历是一个关键码单调递增的节点序列。

二叉查找树的存储

    用数组模拟二叉树

 struct node {
     int l, r;//左右子节点在数组中的下标
     int val;//节点关键码
 }tree[Size];//数组模拟链表
 int tot;//使用过和正在使用的节点总数量
 int root;//当前根节点编号，即数组下标

优点：编程复杂度低。不需要考虑分配内存和回收内存

缺点：内存利用率低

用指针表示二叉树

 struct node {
     node *l, *r; //指向左右儿子
     int val;//节点关键码
 }root;

优点：内存利用率高

缺点：编程复杂度高

二叉查找树的操作

    BST支持的操作：

• 树的建立

• 插入关键码为x的节点

• 查询关键码为x的节点的排名

• 求关键码为x的节点的前驱

• 求关键码为x的节点的后继

• 删除关键码为x的节点

二叉查找树的建立

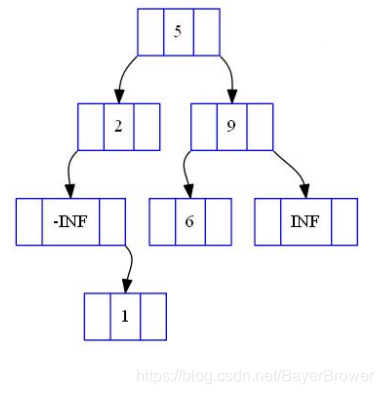
    为了避免越界，减少边界情况的特殊判断，编程实现时一般在 BST中额外插入一个关键码为正无穷和一个关键码为负无穷的节点。 仅由这两个节点构成的BST就是一棵初始的空BST。

int New(int val) {
    a[++tot].val = val;
    return tot;
}
void Build() {
    New(-INF), New(INF);
    root = , a[].r = ;
}

二叉查找树的检索

在BST中检索是否存在关键码为val的节点。 设变量p等于根节点root，执行以下过程：

1.若p的关键码等于val，则已经找到

2.若p的关键码大于val

a.若p的左子节点为空，则说明不存在val

b.若p的左子节点不空，在p的左子树中递归进行检索

3.若瀃的关键码小于val

a.若p的右子节点为空，则说明不存在val

b.若p的右子节点不空，在p的右子树中递归进行检索

在如下BST中：

​

查找6：

​

查找3：

​

 int Get(int p, int val) {
     if (p == ) return ; //检索失败
     if (val == a[p].val) return p; //检索成功
     if (val < a[p].val) return Get(a[p].l, val); //递归检索左子树
     else return Get(a[p].r, val);//递归检索右子树
 }

    二叉查找树的插入

    在BST中插入一个新的值val（假设目前BST中不存在关键码为val的节点， 若存在则不插入），与BST的检索过程类似。

在发现要走向的p的子节点为空，说明val不存在时，直接建立关键码为 val的新节点作为p的子节点。

 void Insert(int &p, int val) {
     if (p == ) {
         p = new(val); //p是引用，其父节点的l或r值会被同时更新
         return;
     }
     if (val == a[p].val) return;
     if (val < a[p].val) Insert(a[p].l, val);
     else Insert(a[p].r, val);
 }

二叉查找树找后继

在BST中， val 的后继指的是在关键码大于 val 的前提下，关键码最小的节点。
初始化val为具有正无穷关键码的那个节点的编号(编号为2)。然后，从根节点开始在BST中检索val。在检索的过程中，每经过一个节点，都检查该节点的关键码，判断能否更新所求的后继val。
检索完成后，有三种可能的结果：
    1.没有找到val此时val的后继就在已经经过的节点中，val即为所求。
    2.找到了关键码为val的节点p，但p没有右子树与上一种情况相同，val即为所求
    3.找到了关键码为val的节点p，且p有右子树从p的右子节点出发，一直向左走，就找到了val的后继

 int GetNext(int val) {
     int ans = ;
     int p = root;
     while (p) {
         if (val == a[p].val) {
             if (a[p].r > ) {
                 p = a[p].r;
                 while (a[p].l > ) p = a[p].l;
                 ans = p;
             }
             break;
         }
         if (a[p].val > val && a[p].val < a[ans].val) ans = p;
         p = val < a[p].val ? a[p].l : a[p].r;
     }
     return a[ans].val;
 }

二叉查找树找前驱

 int GetPre(int val) {
     int ans = ;
     int p = root;
     while (p) {
         if (val == a[p].val) {
             if (a[p].l > ) {
                 p = a[p].l;
                 while (a[p].r > ) p = a[p].r;
                 ans = p;
             }
             break;
         }
         if (a[p].val < val && a[p].val > a[ans].val) ans = p;
         p = val < a[p].val ? a[p].l : a[p].r;
     }
     return a[ans].val;
 }

    二叉查找树的删除

    从BST中删除关键码为val的节点 首先，在BST中检索val，得到节点p 若p的子节点个数小于2，则直接删除p，并令p的子节点代替p的位置，与p 的父节点相连。 若p既有左子树又有右子树，则在BST中求出val的后继节点next。因为next 没有左子树，所以可以直接删除nest，并令next的右子树代替nest的位置。最后， 再让next节点代替p节点，删除p即可。

 void Remove(int val) {
     //检索val， 得到节点p
     int &p = root;
     while (p) {
         if(val == a[p].val) break;
         p = val < a[p].val ? a[p].l : a[p].r;
     }
     if (p == ) return;//结点不存在
     if (a[p].l == ) //没有左子树
         p = a[p].r; //右子树代替p的位置，p是引用
     else if (a[p].r == ) //没有右子树
         p = a[p].l; //左子树代替p的位置，p是引用
     else { //求后继
         int next = a[p].r;
         while (a[next].l > ) next = a[next].l;
         Remove(a[next].val); //next一定没有左子树，直接删除
         a[next].l = a[p].l, a[next].r = a[p].r; //节点next代替p的位置
         p = next;
     }
 }

二叉查找树的性能分析

在随机数据中，BST一次操作的期望复杂度是O(log n)。然而， BST很容易退化，例如在BST中依此插入一个有序序列，将会得到一条 链，平均每次操作的复杂度都为O(n)。 这样的左右子树大小相差很大的BST是不平衡的。有很多种方法可 以维持BST的平衡，从而产生了各种平衡树。

---

THE END