poj1037 [CEOI 2002]A decorative fence 题解

---恢复内容开始---

题意：
t组数据，每组数据给出n个木棒，长度由1到n，除了两端的木棒外，每一根木棒，要么比它左右的两根都长，要么比它左右的两根都短。即要求构成的排列为波浪型。对符合要求的排列按字典序(从左到右，从低到高)进行排序，求排列序号为c的排列。

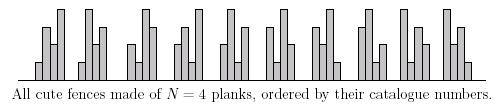
刚拿到这道题时，也是一脸懵逼，感觉起来要用dp，但又不知道从哪里去下手。在网上搜了一下才大概明白。

我们可以先定义状态f[i]表示第i个木棒的合法方案数，我们考虑去转移，怎么从f[i-j]转移到f[i]呢？我们就要考虑第i-j个木棒的长度以及第i个木棒的长度关系，我们把下降的方案称为down,上升的称为up,我们将i根木棒构成的合法集合称为S(i)。

我们在选定x作为第一根木棒之后，去选择第二个木棒y，此时我们要去考虑x,y的长度关系，而在选定y之后我们又要考虑y和下一根木棒长度的关系，并且当方案不符合时我们也不便于去重新选择，此时我们的方程很难进行转移。

我们便可以考虑在此基础上进行细化f[i]=f[i][k] (k=1....i)

我们再定义状态f[i][j]表示集合S(i)中以第j短的木棒为第一个的方案数那么我们便可以写出状态转移方程

f[i][j]= \(\sum_{m=j}^p\) f[i][m] (down) + \(\sum_{n=1}^q\) f[i][n] (up) (p=i-1,q=j-1)

我们发现这个方程仍然不好转移，因为它还是没有拜托前面的约束。我们便可在问题上再进行细分

f[i][j]=f[i][j][down]+f[i][j][up]

f[i][j][[down]表示i根木棒以第j短的木棒为首的下降方案数，我们再去考虑状态转移方程

f[i[[j][down]= \(\sum_{n=1}^q\)f[i-1][n][up]

f[i[[j][up]= \(\sum_{m=j}^p\)f[i-1][m][down]

(p=i-1,q=j-1)

至此我们可以得出一个技巧，当在做dp类型的题目时，状态不好进行转移时我们可以在此基础上增加一维，如blocks，便于转移

至此问题还并没有得到解决，题目要求序列为c的方案，那么我们又改如何去求到呢？我们考虑以第1短的木棒为第一个的方案p(1)，若c>p(1）则说明c不在p(1)之中,c减去p(1),我们再去考虑p(2),若还大于,则类推，当c<=p(k)时我们便可确定c在以第k短的木棒为第一根的集合内，我们再去考虑第二根,以此类推下去,求得解。

代码

#include<bits/stdc++.h>
using namespace std;
int T,n,used[25];
long long f[25][25][2],c;//0->up,1->down
void sta(int n){
	memset(f,0,sizeof(f));
	f[1][1][0]=f[1][1][1]=1;
	for(int i=2;i<=n;++i){
		for(int j=1;j<=i;++j){
			for(int M=j;M<i;++M) f[i][j][0]+=f[i-1][M][1];
			for(int N=1;N<j;++N) f[i][j][1]+=f[i-1][N][0];
		}
	}
}
void print(int n,long long cc){
	long long jump=0;
	int a[25];
	memset(used,0,sizeof(used));
	for(int i=1;i<=n;++i){
		long long tmp=jump;
		int k,p=0;
		for(k=1;k<=n;++k){
			tmp=jump;
			if(!used[k]){
				++p;
				if(i==1) jump+=f[n][p][1]+f[n][p][0];
				else{
					if(k>a[i-1]&&(i<=2||a[i-2]>a[i-1])) jump+=f[n-i+1][p][1];
					if(k<a[i-1]&&(i<=2||a[i-2]<a[i-1])) jump+=f[n-i+1][p][0];
				}
				if(jump>=cc) break;
			}
		}
		used[k]=1;
		a[i]=k;
		jump=tmp;
	}
	for(int i=1;i<=n;++i){
        printf("%d ",a[i]);
	 	if(i==n) printf("\n");
	}
}
int main(){
	scanf("%d",&T);
	sta(20);
	while(T--){
		scanf("%d %lld",&n,&c);
		print(n,c);
	}
	return 0;
}

---恢复内容结束---