MATLAB实例：PCA降维
MATLAB实例：PCA降维
作者：凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/
1. iris数据
5.1,3.5,1.4,0.2,1
4.9,3.0,1.4,0.2,1
4.7,3.2,1.3,0.2,1
4.6,3.1,1.5,0.2,1
5.0,3.6,1.4,0.2,1
5.4,3.9,1.7,0.4,1
4.6,3.4,1.4,0.3,1
5.0,3.4,1.5,0.2,1
4.4,2.9,1.4,0.2,1
4.9,3.1,1.5,0.1,1
5.4,3.7,1.5,0.2,1
4.8,3.4,1.6,0.2,1
4.8,3.0,1.4,0.1,1
4.3,3.0,1.1,0.1,1
5.8,4.0,1.2,0.2,1
5.7,4.4,1.5,0.4,1
5.4,3.9,1.3,0.4,1
5.1,3.5,1.4,0.3,1
5.7,3.8,1.7,0.3,1
5.1,3.8,1.5,0.3,1
5.4,3.4,1.7,0.2,1
5.1,3.7,1.5,0.4,1
4.6,3.6,1.0,0.2,1
5.1,3.3,1.7,0.5,1
4.8,3.4,1.9,0.2,1
5.0,3.0,1.6,0.2,1
5.0,3.4,1.6,0.4,1
5.2,3.5,1.5,0.2,1
5.2,3.4,1.4,0.2,1
4.7,3.2,1.6,0.2,1
4.8,3.1,1.6,0.2,1
5.4,3.4,1.5,0.4,1
5.2,4.1,1.5,0.1,1
5.5,4.2,1.4,0.2,1
4.9,3.1,1.5,0.1,1
5.0,3.2,1.2,0.2,1
5.5,3.5,1.3,0.2,1
4.9,3.1,1.5,0.1,1
4.4,3.0,1.3,0.2,1
5.1,3.4,1.5,0.2,1
5.0,3.5,1.3,0.3,1
4.5,2.3,1.3,0.3,1
4.4,3.2,1.3,0.2,1
5.0,3.5,1.6,0.6,1
5.1,3.8,1.9,0.4,1
4.8,3.0,1.4,0.3,1
5.1,3.8,1.6,0.2,1
4.6,3.2,1.4,0.2,1
5.3,3.7,1.5,0.2,1
5.0,3.3,1.4,0.2,1
7.0,3.2,4.7,1.4,2
6.4,3.2,4.5,1.5,2
6.9,3.1,4.9,1.5,2
5.5,2.3,4.0,1.3,2
6.5,2.8,4.6,1.5,2
5.7,2.8,4.5,1.3,2
6.3,3.3,4.7,1.6,2
4.9,2.4,3.3,1.0,2
6.6,2.9,4.6,1.3,2
5.2,2.7,3.9,1.4,2
5.0,2.0,3.5,1.0,2
5.9,3.0,4.2,1.5,2
6.0,2.2,4.0,1.0,2
6.1,2.9,4.7,1.4,2
5.6,2.9,3.6,1.3,2
6.7,3.1,4.4,1.4,2
5.6,3.0,4.5,1.5,2
5.8,2.7,4.1,1.0,2
6.2,2.2,4.5,1.5,2
5.6,2.5,3.9,1.1,2
5.9,3.2,4.8,1.8,2
6.1,2.8,4.0,1.3,2
6.3,2.5,4.9,1.5,2
6.1,2.8,4.7,1.2,2
6.4,2.9,4.3,1.3,2
6.6,3.0,4.4,1.4,2
6.8,2.8,4.8,1.4,2
6.7,3.0,5.0,1.7,2
6.0,2.9,4.5,1.5,2
5.7,2.6,3.5,1.0,2
5.5,2.4,3.8,1.1,2
5.5,2.4,3.7,1.0,2
5.8,2.7,3.9,1.2,2
6.0,2.7,5.1,1.6,2
5.4,3.0,4.5,1.5,2
6.0,3.4,4.5,1.6,2
6.7,3.1,4.7,1.5,2
6.3,2.3,4.4,1.3,2
5.6,3.0,4.1,1.3,2
5.5,2.5,4.0,1.3,2
5.5,2.6,4.4,1.2,2
6.1,3.0,4.6,1.4,2
5.8,2.6,4.0,1.2,2
5.0,2.3,3.3,1.0,2
5.6,2.7,4.2,1.3,2
5.7,3.0,4.2,1.2,2
5.7,2.9,4.2,1.3,2
6.2,2.9,4.3,1.3,2
5.1,2.5,3.0,1.1,2
5.7,2.8,4.1,1.3,2
6.3,3.3,6.0,2.5,3
5.8,2.7,5.1,1.9,3
7.1,3.0,5.9,2.1,3
6.3,2.9,5.6,1.8,3
6.5,3.0,5.8,2.2,3
7.6,3.0,6.6,2.1,3
4.9,2.5,4.5,1.7,3
7.3,2.9,6.3,1.8,3
6.7,2.5,5.8,1.8,3
7.2,3.6,6.1,2.5,3
6.5,3.2,5.1,2.0,3
6.4,2.7,5.3,1.9,3
6.8,3.0,5.5,2.1,3
5.7,2.5,5.0,2.0,3
5.8,2.8,5.1,2.4,3
6.4,3.2,5.3,2.3,3
6.5,3.0,5.5,1.8,3
7.7,3.8,6.7,2.2,3
7.7,2.6,6.9,2.3,3
6.0,2.2,5.0,1.5,3
6.9,3.2,5.7,2.3,3
5.6,2.8,4.9,2.0,3
7.7,2.8,6.7,2.0,3
6.3,2.7,4.9,1.8,3
6.7,3.3,5.7,2.1,3
7.2,3.2,6.0,1.8,3
6.2,2.8,4.8,1.8,3
6.1,3.0,4.9,1.8,3
6.4,2.8,5.6,2.1,3
7.2,3.0,5.8,1.6,3
7.4,2.8,6.1,1.9,3
7.9,3.8,6.4,2.0,3
6.4,2.8,5.6,2.2,3
6.3,2.8,5.1,1.5,3
6.1,2.6,5.6,1.4,3
7.7,3.0,6.1,2.3,3
6.3,3.4,5.6,2.4,3
6.4,3.1,5.5,1.8,3
6.0,3.0,4.8,1.8,3
6.9,3.1,5.4,2.1,3
6.7,3.1,5.6,2.4,3
6.9,3.1,5.1,2.3,3
5.8,2.7,5.1,1.9,3
6.8,3.2,5.9,2.3,3
6.7,3.3,5.7,2.5,3
6.7,3.0,5.2,2.3,3
6.3,2.5,5.0,1.9,3
6.5,3.0,5.2,2.0,3
6.2,3.4,5.4,2.3,3
5.9,3.0,5.1,1.8,3
2. MATLAB程序
function [COEFF,SCORE,latent,tsquared,explained,mu,data_PCA]=pca_demo()
x=load('iris.data');
[~,d]=size(x);
k=d-1; %前k个主成分
x=zscore(x(:,1:d-1)); %归一化数据
[COEFF,SCORE,latent,tsquared,explained,mu]=pca(x);
% 1）获取样本数据 X ，样本为行，特征为列。
% 2）对样本数据中心化，得S（S = X的各列减去各列的均值）。
% 3）求 S 的协方差矩阵 C = cov(S)
% 4) 对协方差矩阵 C 进行特征分解 [P,Lambda] = eig(C);
% 5）结束。
% 1、输入参数 X 是一个 n 行 p 列的矩阵。每行代表一个样本观察数据，每列则代表一个属性，或特征。
% 2、COEFF 就是所需要的特征向量组成的矩阵，是一个 p 行 p 列的矩阵，没列表示一个出成分向量，经常也称为（协方差矩阵的）特征向量。并且是按照对应特征值降序排列的。所以，如果只需要前 k 个主成分向量，可通过：COEFF(:,1:k) 来获得。
% 3、SCORE 表示原数据在各主成分向量上的投影。但注意：是原数据经过中心化后在主成分向量上的投影。即通过：SCORE = x0*COEFF 求得。其中 x0 是中心平移后的 X（注意：是对维度进行中心平移，而非样本。），因此在重建时，就需要加上这个平均值了。
% 4、latent 是一个列向量，表示特征值，并且按降序排列。
% 5、tsquared Hotelling的每个观测值X的T平方统计量
% 6、explained 由每个主成分解释的总方差的百分比
% 7、mu 每个变量X的估计平均值
% x= bsxfun(@minus,x,mean(x,1));
data_PCA=x*COEFF(:,1:k);
latent1=100*latent/sum(latent);%将latent总和统一为100，便于观察贡献率
pareto(latent1);%调用matla画图 pareto仅绘制累积分布的前95%，因此y中的部分元素并未显示
xlabel('Principal Component');
ylabel('Variance Explained (%)');
% 图中的线表示的累积变量解释程度
print(gcf,'-dpng','Iris PCA.png');
iris_pac=data_PCA(:,1:2) ;
save iris_pca iris_pac
3. 结果
iris_pca：前两个主成分
-2.25698063306803 0.504015404227653
-2.07945911889541 -0.653216393612590
-2.36004408158421 -0.317413944570283
-2.29650366000389 -0.573446612971233
-2.38080158645275 0.672514410791076
-2.06362347633724 1.51347826673567
-2.43754533573242 0.0743137171331950
-2.22638326740708 0.246787171742162
-2.33413809644009 -1.09148977019584
-2.18136796941948 -0.447131117450110
-2.15626287481026 1.06702095645556
-2.31960685513084 0.158057945820095
-2.21665671559727 -0.706750478104682
-2.63090249246321 -0.935149145374822
-2.18497164997156 1.88366804891533
-2.24394778052703 2.71328133141014
-2.19539570001472 1.50869601039751
-2.18286635818774 0.512587093716441
-1.88775015418968 1.42633236069007
-2.33213619695782 1.15416686250116
-1.90816386828207 0.429027879924458
-2.19728429051438 0.949277150423224
-2.76490709741649 0.487882574439700
-1.81433337754274 0.106394361814184
-2.22077768737273 0.161644638073716
-1.95048968523510 -0.605862870440206
-2.04521166172712 0.265126114804279
-2.16095425532709 0.550173363315497
-2.13315967968331 0.335516397664229
-2.26121491382610 -0.313827252316662
-2.13739396044139 -0.482326258880086
-1.82582143036022 0.443780130732953
-2.59949431958629 1.82237008322707
-2.42981076672382 2.17809479520796
-2.18136796941948 -0.447131117450110
-2.20373717203888 -0.183722323644913
-2.03759040170113 0.682669420156327
-2.18136796941948 -0.447131117450110
-2.42781878392261 -0.879223932713649
-2.16329994558551 0.291749566745466
-2.27889273592867 0.466429134628597
-1.86545776627869 -2.31991965918865
-2.54929404704891 -0.452301129580194
-1.95772074352968 0.495730895348582
-2.12624969840005 1.16752080832811
-2.06842816583668 -0.689607099127106
-2.37330741591874 1.14679073709691
-2.39018434748641 -0.361180775489047
-2.21934619663183 1.02205856145225
-2.19858869176329 0.0321302060908945
1.10030752013391 0.860230593245533
0.730035752246062 0.596636784545418
1.23796221659453 0.612769614333371
0.395980710562889 -1.75229858398514
1.06901265623960 -0.211050862633647
0.383174475987114 -0.589088965722193
0.746215185580377 0.776098608766709
-0.496201068006129 -1.84269556949638
0.923129796737431 0.0302295549588077
0.00495143780650871 -1.02596403732389
-0.124281108093219 -2.64918765259090
0.437265238506424 -0.0586846858581760
0.549792126592992 -1.76666307900171
0.714770518429262 -0.184815166484382
-0.0371339806719297 -0.431350035919633
0.872966018474250 0.508295314415273
0.346844440799832 -0.189985178614466
0.152880381053472 -0.788085297090142
1.21124542423444 -1.62790202112846
0.156417163578196 -1.29875232891050
0.735791135537219 0.401126570248885
0.470792483676532 -0.415217206131680
1.22388807504403 -0.937773165086814
0.627279600231826 -0.415419947028686
0.698133985336190 -0.0632819273014206
0.870620328215835 0.249871517845242
1.25003445866275 -0.0823442389434431
1.35370481019450 0.327722365822153
0.659915359649250 -0.223597000167979
-0.0471236447211597 -1.05368247816741
0.121128417400412 -1.55837168956507
0.0140710866007487 -1.56813894313840
0.235222818975321 -0.773333046281646
1.05316323317206 -0.634774729305402
0.220677797156699 -0.279909968621073
0.430341476713787 0.852281697154445
1.04590946111265 0.520453696157683
1.03241950881290 -1.38781716762055
0.0668436673617666 -0.211910813930204
0.274505447436587 -1.32537578085168
0.271425764670620 -1.11570381243558
0.621089830946741 0.0274506709978046
0.328903506457842 -0.985598883763833
-0.372380114621411 -2.01119457605980
0.281999617970590 -0.851099454545845
0.0887557702224096 -0.174324544331148
0.223607676665854 -0.379214256409087
0.571967341693057 -0.153206717308028
-0.455486948803962 -1.53432438068788
0.251402252309636 -0.593871222060355
1.84150338645482 0.868786147264828
1.14933941416981 -0.698984450845645
2.19898270027627 0.552618780551384
1.43388176486790 -0.0498435417617587
1.86165398830779 0.290220535935809
2.74500070081969 0.785799704159685
0.357177895625210 -1.55488557249365
2.29531637451915 0.408149356863061
1.99505169024551 -0.721448439846371
2.25998344407884 1.91502747107928
1.36134878398531 0.691631011499905
1.59372545693795 -0.426818952656741
1.87796051113409 0.412949339203311
1.24890257443547 -1.16349352357816
1.45917315700813 -0.442664601834978
1.58649439864337 0.674774813132046
1.46636772102851 0.252347085727036
2.42924030093571 2.54822056527013
3.29809226641255 -0.00235343587272177
1.24979406018816 -1.71184899071237
2.03368323142868 0.904369044486726
0.970663302005081 -0.569267277965818
2.88838806680663 0.396463170625287
1.32475563655861 -0.485135293486995
1.69855040646181 1.01076227706927
1.95119099025002 0.999984474306318
1.16799162725452 -0.317831851008113
1.01637609822602 0.0653241212065782
1.78004554289349 -0.192627479858818
1.85855159177699 0.553527164026207
2.42736549094542 0.245830911619345
2.30834922706014 2.61741528404554
1.85415981777379 -0.184055790370030
1.10756129219332 -0.294997832217552
1.19347091639304 -0.814439294423699
2.79159729280499 0.841927657717863
1.57487925633390 1.06889360300461
1.34254676764379 0.420846092290459
0.920349720485088 0.0191661621187343
1.84736314547313 0.670177571688802
2.00942543830962 0.608358978317639
1.89676252747561 0.683734258412757
1.14933941416981 -0.698984450845645
2.03648602144585 0.861797777652503
1.99500750598298 1.04504903502442
1.86427657131500 0.381543630923962
1.55328823048458 -0.902290843047121
1.51576710303099 0.265903772450991
1.37179554779330 1.01296839034343
0.956095566421630 -0.0222095406309480
累计贡献率
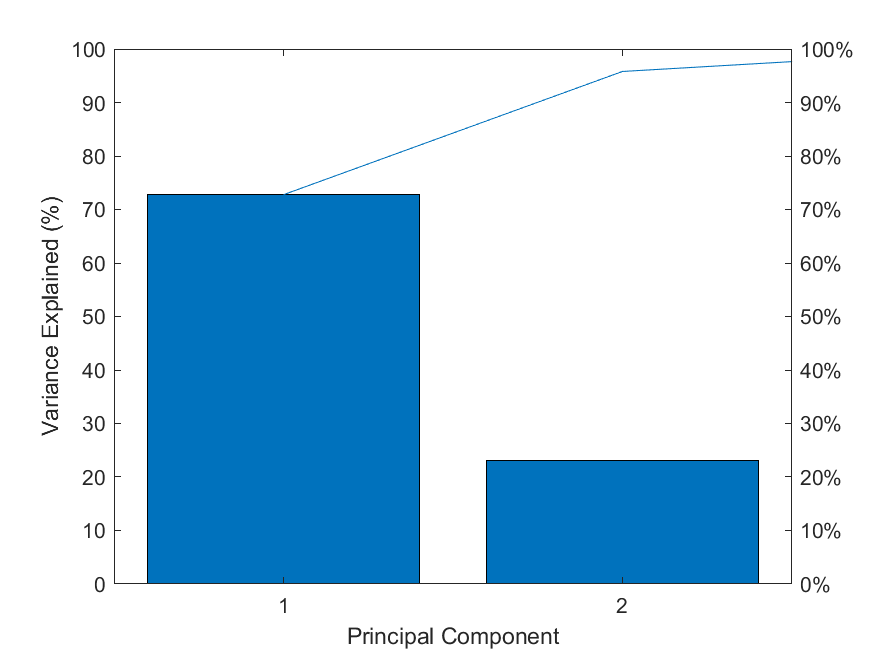
可见：前两个主成分已经占了95%的贡献程度。这两个主成分可以近似表示整个数据。
4. pca_data.m
其中normlization.m见MATLAB实例：聚类初始化方法与数据归一化方法
function data=pca_data(data, choose)
% PCA降维，保留90%的特征信息
data = normlization(data, choose); %归一化
score = 0.90; %保留90%的特征信息
[num,dim] = size(data);
xbar = mean(data,1);
means = bsxfun(@minus, data, xbar);
cov = means'*means/num;
[V,D] = eig(cov);
eigval = diag(D);
[~,idx] = sort(eigval,'descend');
eigval = eigval(idx);
V = V(idx,:);
p = 0;
for i=1:dim
perc = sum(eigval(1:i))/sum(eigval);
if perc > score
p = i;
break;
end
end
E = V(1:p,:);
data= means*E';
参考：
Junhao Hua. Distributed Variational Bayesian Algorithms. Github, 2017.
MATLAB实例：PCA降维的更多相关文章
- MATLAB实例：PCA（主成成分分析）详解
MATLAB实例:PCA(主成成分分析)详解 作者:凯鲁嘎吉 - 博客园 http://www.cnblogs.com/kailugaji/ 1. 主成成分分析 2. MATLAB解释 详细信息请看: ...
- PCA降维2
前言 本文为模式识别系列第一篇,主要介绍主成分分析算法(Principal Component Analysis,PCA)的理论,并附上相关代码.全文主要分六个部分展开: 1)简单示例.通过简单的例子 ...
- [综] PCA降维
http://blog.json.tw/using-matlab-implementing-pca-dimension-reduction 設有m筆資料, 每筆資料皆為n維, 如此可將他們視為一個mx ...
- 机器学习公开课笔记(8)：k-means聚类和PCA降维
K-Means算法 非监督式学习对一组无标签的数据试图发现其内在的结构,主要用途包括: 市场划分(Market Segmentation) 社交网络分析(Social Network Analysis ...
- Python机器学习笔记 使用scikit-learn工具进行PCA降维
之前总结过关于PCA的知识:深入学习主成分分析(PCA)算法原理.这里打算再写一篇笔记,总结一下如何使用scikit-learn工具来进行PCA降维. 在数据处理中,经常会遇到特征维度比样本数量多得多 ...
- PCA降维—降维后样本维度大小
之前对PCA的原理挺熟悉,但一直没有真正使用过.最近在做降维,实际用到了PCA方法对样本特征进行降维,但在实践过程中遇到了降维后样本维数大小限制问题. MATLAB自带PCA函数:[coeff, sc ...
- 一步步教你轻松学主成分分析PCA降维算法
一步步教你轻松学主成分分析PCA降维算法 (白宁超 2018年10月22日10:14:18) 摘要:主成分分析(英语:Principal components analysis,PCA)是一种分析.简 ...
- PCA 降维算法详解 以及代码示例
转载地址:http://blog.csdn.net/watkinsong/article/details/38536463 1. 前言 PCA : principal component analys ...
- PCA降维技术
PCA降维技术 PCA 降维 Fly Time: 2017-2-28 主成分分析(PCA) PCA Algorithm 实例 主成分分析(PCA) 主成分分析(Principal Component ...
随机推荐
- Jupyter Notebooks的安装和使用介绍
最近又开始重新学习Python,学习中使用到了一款编辑器Jupyter Notebooks ,非常想安利给初学python的同学.注:本文内容仅针对windows环境下安装和配置Jupyter Not ...
- WePy框架的使用
基本示例 import wepy from 'wepy';//引入wepy框架说明 // 通过继承自wepy.page的类创建页面逻辑 export default class Index exten ...
- How To Restore Rman Backups On A Different Node When The Directory Structures Are Different (Doc ID 419137.1)
How To Restore Rman Backups On A Different Node When The Directory Structures Are Different (Doc ID ...
- MyBatis中特殊符号的转义
在MyBatis中遇到特殊符号时有两种转义方式: 第一种 描述 空格 小于 大于 小于等于 大于等于 与 单引号 双引号 原符号 < > <= >= & ' " ...
- 201871010116-祁英红《面向对象程序设计（java）》第八周学习总结
项目 内容 <面向对象程序设计(java)> https://home.cnblogs.com/u/nwnu-daizh/ 这个作业的要求在哪里 https://www.cnblogs.c ...
- Codeforces Round #594 (Div. 2) A. Integer Points 水题
A. Integer Points DLS and JLS are bored with a Math lesson. In order to entertain themselves, DLS to ...
- Luogu P5368 [PKUSC2018]真实排名
老年选手只会做SB题了(还调了好久) 很容易想到分类讨论,按第\(i\)个人有没有翻倍来算 若\(a_i\)未翻倍,显然此时将\([0,\lceil \frac{a_i}{2}\rceil)\)的数和 ...
- idea配置pyspark
默认python已经配好,并已经导入idea,只剩下pyspark的安装 1.解压spark-2.1.0-bin-hadoop2.7放入磁盘目录 D:\spark-2.1.0-bin-hadoop2. ...
- 【linux运维】linux系统上忘记密码如何操作
目录 红帽系统忘记密码操作 红帽系统设置ip,主机名 centos系统忘记密码操作 一.红帽系统忘记密码操作 1)再出现以下界面后按键盘e键 2)进入以下界面后,再次按e键 3)使用上下键选择第2项或 ...
- Redis for OPS 02：消息订阅和事务管理
写在前面的话 上一节谈了 Redis 的安装以及五种基本数据类型的一些简单的操作,本章节主要看看 Redis 的另外一些特征,虽然可能不常用,但是还是需要了解的.对于我们运维人员来讲,这些东西更像拓展 ...