三、排序算法总结一（冒泡排序，插入排序，选择排序）（C++版本）

一、引言

　　对于各种排序算法也算是有了一定的了解，所以这里做一个总结。

二、冒泡排序法。

这是比较经典的排序算法，主要是通过内外两层的循环比较，使得乱序变为顺序。

　　下面是一个测试代码

 #include <iostream>
 #include <vector>
 using namespace std;
 int main()
 {
     vector<int> L();
     for(int i=;i<L.size();i++)
     {
         L[i] =  - i;
     }
     int temp = ;
     for (int i = ; i < L.size(); i++)
         for (int j = L.size()-; j >= (i+); j--)
         {
             if (L[j-] > L[j ])
             {
                 temp = L[j];
                 L[j] = L[j - ];
                 L[j - ] = temp;
             }
         }
     for (int j = ; j < L.size(); j++)
     {
         cout << "the number is " << L[j] << endl;
     }
 }

　　初始化为10-1，最后冒泡排序法的的结果为升序排列。

　　下面是算法的运行过程。

　　在第一次循环里面（即i=0的时候）：

　　每一次比较之后数据变化如下：

　　

随着 i 的增大，蓝色区域扩展如下：

　　

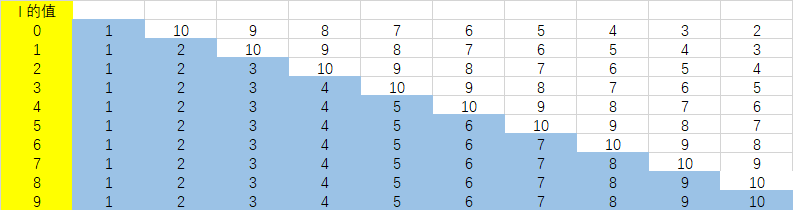
　　最后达到有序状态。

　　从上面的分析可以看出来：

　　其时间复杂度：O(n ²) (这里的时间，主要花费在了比较运算上面，所以计算的是循环里面的比较次数)

　　空间复杂度： O(n)  （即所有的变量占用的空间）

　　算法稳定性上来说，属于稳定算法（即两个相同的元素经过排序之后的 先后顺序不变）。

二直接插入排序

　　插入排序的算法思想是，将待排序的数据看做两个部分，一部分是有序数据A,一部分是无序数据B, 最开始的时候A的规模是0， B是整个的待排序数据。

　　之后对于B中的每一个数据，按照顺序插入到A中，直至整个过程完成。

　　例如，对于一个待排序数组来说，过程如下：

　　

#include <iostream>
using namespace std;
void Sorted(int* x, int length);
int main(void)
{
    int a[]={,,,,};
    Sorted(a,);
    for(int i=;i<;i++)
        cout<<"-----------"<<a[i]<<endl;
    return ;
}

void Sorted(int* x, int length)
{
    for(int i=; i<length;i++ )
    {
        int temp=x[i];
        int j=i-;
        while( j>= && temp<x[j])
        {
            x[j+]=x[j];
            x[j]=temp;
            j--;
        }
     }
}

　　在上面的例子里面：

 a[]={,,,,};

　　在每一步的运算过程中，其数据的变化如下：

   

　

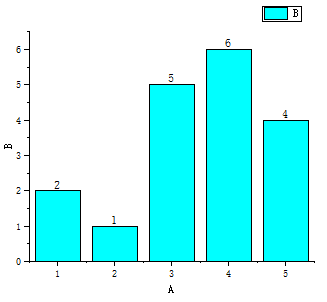
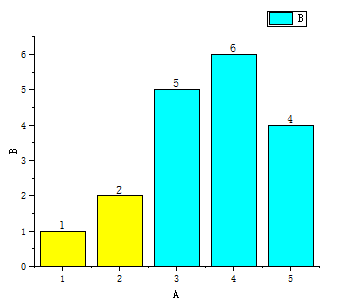
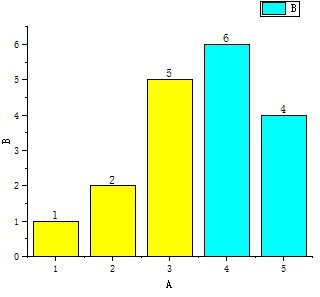
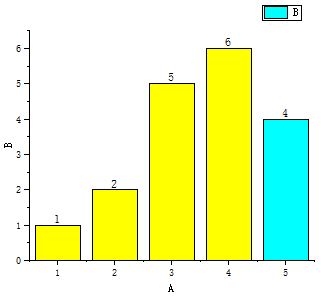
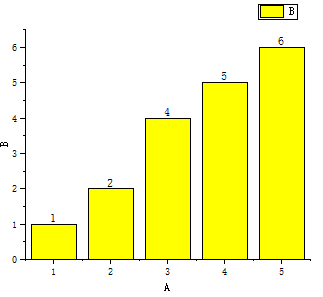
　　上述描述了比较的过程。

　　柱状图表表示了每一个位置的数字大小，蓝色区域为无序部分，黄色部分为经过一次运算之后的有序部分。

　　其主要步骤是，选择无序部分的第一个元素，将其插入到黄色的有序部分里面去，这样黄色区域扩展，而蓝色区域则是不断地减小，直至所有的区域变为有序状态。

复杂度分析：

　　可以看到，上述过程，主要操作是比较操作，然后是赋值操作,其中赋值操作的所花费的时间更长

　　在最好的情况下，整个数据正好是升序排列的，这个时候比较操作是（n-1），赋值操作 复杂度为0

　　在最坏的情况下，整个数据是降序排列的，这个时候比较次数是  n*(n-1)/2 次，赋值操作是4*n*(n-1)/2, 主要的时间花在了赋值的操作上，时间复杂度为O(n²)

　　稳定性来说，这个算法是不稳定的，即相同的两个元素，在排序前和排序之后，先后次序可能发生了改变。

三、选择排序

　　选择排序的思想与上面的插入排序相同，将数据分为有序部分和无序部分。

　　在无序部分里面选择出最值（比如说是最大值，放到有序部分），这样经过不断的选择无序部分的最大值，使得有序部分不断的扩展，无序部分不断地缩小，最后得到整个有序数据序列。

　　具体代码如下：

 #include <iostream>
 using namespace std;
 void Sorted(int* x, int length);
 int main(void)
 {
     int a[] = { ,,,,};
     Sorted(a, );
     for (int i = ; i < ; i++)
         cout << "-----------" << a[i] << endl;
     return ;
 }

 void Sorted(int* x, int length)
 {
     int max = ;
     int len = length - ;

     for (int i = ; i <= length-; i=i+)
     {
         max = x[];
         int j = ;
         int number = ;
         for (j = ; j <= len; j++)
         {
             if (max < x[j])
             {
                 max = x[j];
                 number = j;
             }
         }
         int temp = x[len];
         x[len] = max;
         x[number] = temp;
         len--;
     }
 }

其每一次的比较过程如下：

 

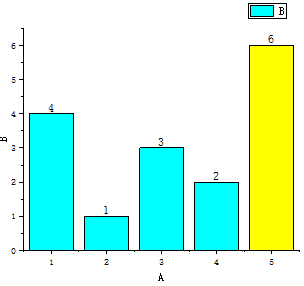
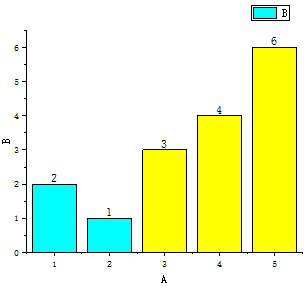
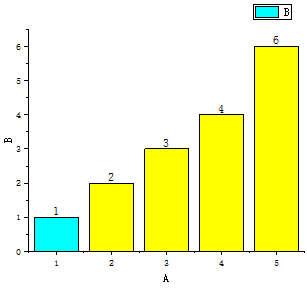
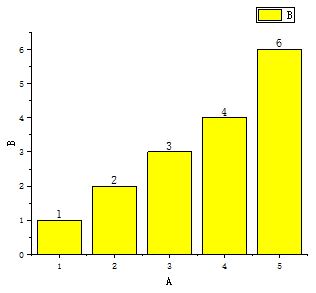
如图可以看到，有序的黄色区域在不断的扩展，无序部分在逐渐减少。

复杂度：

　　最好情况：全是升序排列，这个时候只需要(n-1)次比较

　　最坏情况：全是降序排列，这个时候需要（n-1)*n/2次比较，（n-1）次互换操作，时间复杂度在O(n) （这里只是考虑了互换操作）, 比冒泡排序法快

　　稳定性：不稳定