[Luogu P3338] [ZJOI2014]力 (数论 FFT 卷积)

题面

传送门：

• 洛咕
• BZOJ

---

Solution

写到脑壳疼，我好菜啊

我们来颓柿子吧

\(F_j=\sum_{i<j}\frac{q_i*q_j}{(i-j)^2}-\sum_{i>j}\frac{q_i*q_j}{(i-j)^2}\)

\(q_j\)与\(i\)没有半毛钱关系，提到外面去

\(F_j=q_j*\sum_{i<j}\frac{q_i}{(i-j)^2}-q_j*\sum_{i>j}\frac{q_i}{(i-j)^2}\)

左右同时除以\(q_j\)

\(E_j=\sum_{i=1}^{j-1}\frac{q_i}{(i-j)^2}-\sum_{i=j+1}^{n}\frac{q_i}{(i-j)^2}\)

我们设\(f(i)=q(i),g(i)=\frac{1}{i^2}\)，有

\(E_j=\sum_{i=1}^{j-1}f(i)*g(i-j)-\sum_{i=j+1}^{n}f(i)*g(i-j)\)

因为\(g(i)\)是个偶函数，因此有：

\(E_j=\sum_{i=1}^{j-1}f(i)*g(j-i)-\sum_{i=j+1}^{n}f(i)*g(i-j)\)

这时候，我们显然可以发现左边那个式子是个卷积，右边的这样一波化简就也变成了卷积形式：

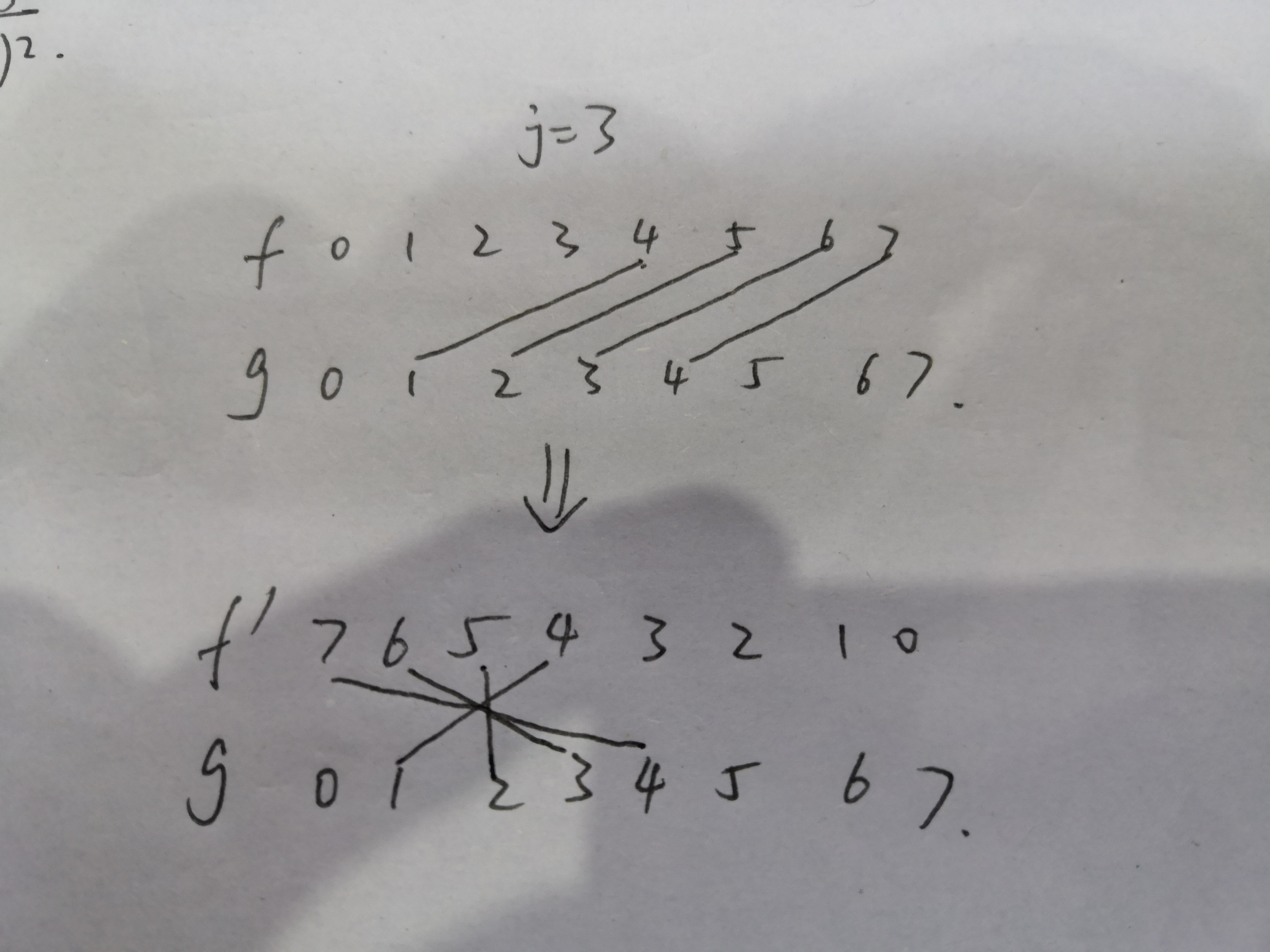
卷积用FFT快速计算即可

时间复杂度\(O(nlogn)\)

---

Code

//Luogu P3338 [ZJOI2014]力
//Jan,18th,2019
//FFT加速卷积
#include<iostream>
#include<cstdio>
#include<cmath>
#include<algorithm>
#include<complex>
using namespace std;
typedef complex <double> cp;
const double PI=acos(-1);
const int M=100000+100;
const int N=8*M;
inline cp omega(int K,int n)
{
	return cp(cos(2*PI*K/n),sin(2*PI*K/n));
}
void FFT(cp a[],int n,bool type)
{
	static int len=0,num=n-1,t[N];
	while(num!=0) len++,num/=2;
	for(int i=0,j;i<=n;i++)
	{
		for(j=0,num=i;j<len;j++)
			t[j]=num%2,num/=2;
		reverse(t,t+len);
		for(j=0,num=0;j<len;j++)
			num+=t[j]*(1<<j);
		if(i<num) swap(a[i],a[num]);
	}
	for(int l=2;l<=n;l*=2)
	{
		int m=l/2;
		cp x0=omega(1,l);
		if(type==true) x0=conj(x0);
		for(int j=0;j<n;j+=l)
		{
			cp x=cp(1,0);
			for(int k=0;k<m;k++,x*=x0)
			{
				cp temp=x*a[j+k+m];
				a[j+k+m]=a[j+k]-temp;
				a[j+k]=a[j+k]+temp;
			}
		}
	}
}
int n,m;
double q[N];
cp f[N],g[N],f2[N];
int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%lf",&q[i]);

	for(int i=1;i<=n;i++)
		g[i]=(1.0/i/i);
	m=1;
	while(m<2*n) m*=2;
	for(int i=1;i<m;i++)
		f[i]=q[i],f2[i]=q[i];

	FFT(g,m,false);
	FFT(f,m,false);
	reverse(f2+1,f2+n+1);
	FFT(f2,m,false);
	for(int i=0;i<m;i++)
		f[i]*=g[i],f2[i]*=g[i];
	FFT(f,m,true);
	FFT(f2,m,true);

	for(int i=1;i<=n;i++)
		printf("%lf\n",(f[i].real()-f2[n-i+1].real())/m);
	return 0;
}