ACM-ICPC 2017 Asia Xi'an

ACM-ICPC 2017 Asia Xi'an

Solved	A	B	C	D	E	F	G	H	I	J	K
7/11	O	O			Ø	O	O	?		O	O

• O for passing during the contest
• Ø for passing after the contest
• ! for attempted but failed
• · for having not attempted yet

A - XOR

计蒜客 - A1607

solved by hyd+dyp

题意：长度为\(n\)的数组\(a\)，\(q\)次询问，每次询问给出 \(l\)，\(r\)，问从\(a[l],a[l+1],\cdots a[r]\)中取出若干个数字，使得其异或和跟一个固定数字$ k$ 进行或运算所得结果的最大值。\(n\le 10000,q\le 100000,k\le100000, a[i]\le 1e8\)

分析：区间内选出若干个数字的异或和，我们先不考虑跟固定数值 k 的运算，如果要从中选出最大的异或和，很容易想到前缀线性基求解（或者是线段树合并线性基），在线性基里面按位查找即可得到最大值。

贪心的维护序列的前缀线性基（上三角形态），对于每个线性基，将出现位置靠右的数字尽可能地放在高位，也就是说在插入新数字的时候，要同时记录对应位置上数字的出现位置，并且在找到可以插入的位置的时候，如果新数字比位置上原来的数字更靠右，就将该位置上原来的数字向低位推。

在求最大值时候，从高位向低位遍历，如果该位上的数字出现在询问中区间左端点的右侧且可以使答案变得更大，就异或到答案里面。

到这里可以顺便看看这个题：链接, 你或许可以直接把他A掉。

然后再考虑跟固定 k 的操作，我们知道 k 的二进制表示中，那些为 1 的位是没有用的，因为最终求出来的异或和要跟 k 进行或运算，所以除去这些位，我们应当贪心的去考虑高位（这与普通线性基插入时优先考虑高位是一样的），并且忽略掉 k 的二进制中为 1 的那些位。

为什么要这么考虑呢？如果在插入某个数到线性基之前，不考虑 k 的因素而直接贪心的插入，那么线性基中为了可以异或出更大的值，某个数字可能会以较高的优先级插入到某个高位，而这一位可能对于 k 来说已经没有任何用了。

举个例子，如果线性基中有这么两个数字：1001，0111，k 为 1000。那么直接构建线性基从中得到最大值为 1110，跟 k 或得到 1110，而答案应该是：1111

const int N = 100000 + 5;
int T, n, q, k;
int a[N];
struct Base{
    int a[31];
    int pos[31];
    int cnt;
    Base(){
        cnt =0;memset(a,0,sizeof a);
        memset(pos, 0, sizeof pos);
    }
    void clear(){
        cnt = 0; memset(a, 0, sizeof a);
        memset(pos, 0, sizeof pos);
    }
    bool ins(int x, int id){
        for(int i=29;i>=0;--i){
            if(x >> i & 1){
                if(a[i]){ //如果原来的位置已经有数字了
                    if(id > pos[i]){ //而且当前数字的 id 更大，为了在更高的位保留更靠右出现的数字，下面要做两个数字的交换操作
                        swap(pos[i], id);
                        swap(x, a[i]);
                    }
                    x ^= a[i]; //线性基插入常规操作，保持线性无关
                }
                else {
                    cnt ++;
                    a[i] = x;
                    pos[i] = id;
                    return 1;
                }
            }
        }
        return 0;
    }
}base[N];
int main(){
    int T;scanf("%d",&T);
    while(T--){
        scanf("%d%d%d",&n,&q,&k);
        for(int i=1;i<=n;i++){
            scanf("%d",&a[i]);
            a[i] &= ~k; // k取反后 与运算，去除 k 为 1 的那些位
            base[i] = base[i-1];
            base[i].ins(a[i], i);
        }
        while(q--){
            int l, r;
            scanf("%d%d", &l, &r);
            int res = 0;
            for(int i=29;i>=0;i--){
                //如果该位上面有数字，并且它的出现位置大于等于 l
                if(base[r].a[i] && base[r].pos[i] >= l){
                    //异或后可以使得答案更大，则更新
                    //这里的原因是因为我们维护的是上三角状态，并没有化为最简，可以将第一个样例带入测试
                    if((res ^ base[r].a[i]) > res){
                        res ^= base[r].a[i];
                    }
                }
            }
            res |= k;
            printf("%d\n", res);
        }
    }
    return 0;
}

B - Lovers

计蒜客 - A1608

solved by lwq

从前到后考虑即可，因为它的右边界是单调递增的

const int N = 200000 + 5;
int T, n, k;
int a[N], b[N];
int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d%d", &n, &k);
        for(int i=1;i<=n;i++)scanf("%d", &a[i]);
        for(int i=1;i<=n;i++)scanf("%d", &b[i]);
        sort(a + 1, a + 1 + n);
        sort(b + 1, b + 1 + n);
        int res = 0, l = 1;
        for(int i=n;i>=1;i--){
            while(l <= n && a[l] + b[i] < k) l++;
            if(l <= n) l++, res++;
        }
        printf("%d\n", res);
    }
    return 0;
}

E - Naomi with Graph

计蒜客 - A1611

• 最小割

考虑dist数组，它最终必然满足以下两个条件：

1. \(\forall i \in [1, n], dist[i] \ge 0, dist[1] = 0\)
2. 若原图存在\((u,v)\)这条边，则\(|dist[u]-dist[v]| \le 1\)

对于每个点 \(x\)，分成 \(n\) 个点，连成一条链，头接源点，尾接汇点，从源点到汇点的第 i 个点表示 \(dist[x]\) 的值，那么最终在最小割中，割掉的边就代表着它的最短路长度。

对于原图中存在的边，由于他们存在着\(|dist[u]-dist[v]|\le 1\) 的限制，要对于 \(u\) 和 \(v\) 的两组边进行连边

设函数\(f(x,d) = (d-A[x])^2\)

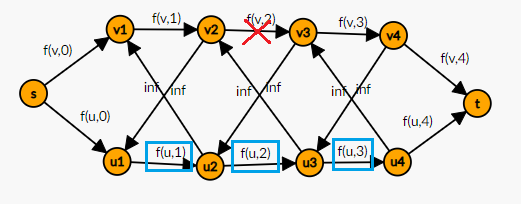
如果最终答案中\(dist[v] = 2\) 那么我们把红叉的边割掉，这就导致了对于 u 这条链，我们只能选择蓝框所选的三条边中的一个，满足了\(|dist[u]-dist[v]|\le 1\)。两组点之间连流量\(\inf\) 是为了防止被割掉，这样的边割掉是没有意义的。

const int N = 10000 + 5;
const int M = 1000010;
vector<int> g[44];
int dist[44], val[44], id[44][44];
int head[N], ver[M], edge[M], nxt[M], d[N];
int n, m, s, t, tot, maxflow;
queue<int> q;
void add(int x, int y, int z){
    ver[++tot] = y, edge[tot] = z, nxt[tot] = head[x], head[x] = tot;
    ver[++tot] = x, edge[tot] = 0, nxt[tot] = head[y], head[y] = tot;
}
bool bfs(bool type){
    memset(d, 0, sizeof d);
    while(q.size())q.pop();
    q.push(s);d[s] = 1;
    while(q.size()){
        int x = q.front();q.pop();
        for(int i=head[x];i;i=nxt[i]){
            if(edge[i] && !d[ver[i]]){
                q.push(ver[i]);
                d[ver[i]] = d[x] + 1;
                if(ver[i] == t) return 1;
            }
        }
    }
    return 0;
}
int dinic(int x, int flow){
    if(x == t) return flow;
    int rest = flow, k;
    for(int i=head[x];i && rest; i=nxt[i]){
       	if(edge[i] && d[ver[i]] == d[x] + 1){
            k = dinic(ver[i], min(rest, edge[i]));
            if(!k) d[ver[i]] = 0;
            edge[i] -= k;
            edge[i ^ 1] += k;
            rest -= k;
        }
    }
    return flow - rest;
}
void bfs(){
    memset(dist, 0, sizeof dist);
    dist[1] = 0;
    queue<int> q;
    q.push(1);
    while(q.size()){
        int x = q.front();q.pop();
        for(int i=0;i<g[x].size();i++){
            int y = g[x][i];
            if(dist[y])continue;
            dist[y] = dist[x] + 1;
            q.push(y);
        }
    }
}
void add(int x){
    for(auto y : g[x]){
        for(int d = 0; d + 1 <n; d++){
            int u = id[y][d+1], v = id[x][d];
            add(u, v, inf);
        }
    }
}
int main(){
    while(~scanf("%d%d", &n,&m)){
        for(int i=1;i<=n;i++) g[i].clear();
        memset(head, 0, sizeof head);
        maxflow = 0;
        tot = 1;
        int cnt = 0;
        for(int i=1;i<=m;i++){
            int x,y;scanf("%d%d", &x,&y);
            g[x].push_back(y);
            g[y].push_back(x);
        }
        bfs();
        for(int i=1;i<=n;i++)scanf("%d", &val[i]);
        for(int i=1;i<=n;i++)for(int j=0;j<n;j++) id[i][j] = ++cnt;
        s = 0, t = cnt + 1;
        for(int i=1;i<=n;i++){
            add(i);
            for(int j=0;j<=n;j++){
                int u, v = id[i][j], z = (val[i]-j)*(val[i]-j);
                u = j == 0 ? s : id[i][j-1];
                if(j == n) v = t;
                if(j > dist[i]) z = inf;
                add(u, v, z);
            }
        }
        int flow = 0;
        while(bfs(1)) while(flow = dinic(s, inf)) maxflow += flow;
        printf("%d\n", maxflow);
    }
    return 0;
}

F - God of Gamblers

计蒜客 - A1612

solved by us

并不会证明，但是感觉上理解就是他们赢的概率都是一样的，并且赌金很公平（都是 k）。所以比的就是两个人继续进行游戏的能力，所以就是 \(\frac{n}{n+m}\)

double n, m;
int main(){
    while(~scanf("%lf%lf",&n,&m)){
        printf("%.5f\n",(n/(n+m)));
    }
    return 0;
}

G - Sum of xor sum

计蒜客 - A1613

solved by hyd

先求出序列的异或前缀和\(s[i] = a[1] ~xor~a[2]~\cdots a[i]\)，可以发现对于每个询问\([l,r]\)， 其实就是求\(s[l-1], s[l],\cdots s[r]\)中每对数的异或，然后取和。

观察到\(a[i]\le 1000000\), 最多20位，所以分 20 位进行考虑，现在区间内变成了两种数字，0，1.

这些数字进行异或，只有 0 与 1 异或可以对答案产生贡献，所以我们只需要维护区间内 1 的个数就好了。

对于二进制的第 k 位，该区间内有\(num1\) 个1，\(num0\) 个0，那么该位对答案的贡献为 \((1<<k)\times num0\times num1\)

(对于这种题，可以拍一些小数据（区间小，数字正常），基本可以防止wa掉)

const int N = 100000 + 5;
const int mod = 1e9 + 7;
int T, n, m, a[N];
int bit[20][N];
ll get(int *s, int l, int r){
    ll num1 = s[r] - s[l-1];
    ll num0 = (r - l + 1) - num1;
    return num0 * num1 % mod;
}
int main(){
    scanf("%d",&T);
    while(T--){
        scanf("%d%d", &n,&m);
        for(int i=1;i<=n;i++){
            scanf("%d", &a[i]);
            for(int j = 0;j < 20;j ++){
                bit[j][i] = a[i] >> j & 1;
            }
        }
        for(int j=0;j<20;j++){
            for(int i=1;i<=n;i++){
                bit[j][i] = bit[j][i-1] ^ bit[j][i];
            }
        }
        for(int j=0;j<20;j++){
            for(int i=1;i<=n;i++){
                bit[j][i] += bit[j][i-1];
            }
        }
        while(m--){
            int l, r;
            scanf("%d%d",&l,&r);
            l--;
            ll res = 0;
            for(int j=0;j<20;j++){
                res = (res + (1ll<<j) * get(bit[j], l, r)%mod)%mod;
            }
            printf("%lld\n", res);
        }
    }
    return 0;
}

H - Arrangement for Contests

计蒜客 - A1614

这个题计蒜客上面的数据有问题，UVALive又挂了，所以代码没有地方测试，思路就是贪心，从前到后只要取，取完之后在该区间内把它减掉即可。线段树维护一下即可

J - LOL

计蒜客 - A1616

solved by hyd+dyp

状压DP

\(d[i][j]\) 表示前 i 个英雄，5个人选或没选的状态是为 j 时的方案数

然后暴力转移即可，跑的飞快（然后N^4暴力枚举算法也能过 dyptql)

复杂度：\(O(10*500*2^5)\)

const int N = 100 + 5;
const int mod = 1e9 + 7;
char S[5][N];
ll d[N][1<<5];
ll A(ll n, ll m){
    ll res = 1;
    for(int i=0;i<m;i++)res = res * (n-i) % mod;
    return res;
}
ll C(ll n, ll m){
    ll res = 1;
    for(int i=0;i<m;i++) res = res * (n - i) ;
    for(int i=1;i<=m;i++) res = res / i ;
    return res %  mod;
}
int main(){
    while(~scanf("%s", S[0]+1)){
        for(int i=1;i<5;i++)scanf("%s", S[i]+1);
        memset(d, 0, sizeof d);
        d[0][0] = 1;
        for(int i = 1;i <= 100; i++){
            for(int j = 0; j < (1<<5); j++){
                //前缀和直接转移
                d[i][j] = (d[i][j] + d[i-1][j]) % mod;
                for(int k = 0; k < 5; k++){
                    if(j >> k & 1)continue;//第 k 个人已经选过
                    if(S[k][i] == '1'){//可以添加新人的转移
                        d[i][j|(1<<k)] = (d[i][j|(1<<k)] + d[i-1][j]) % mod;
                    }
                }
            }
        }
        //为什么Ban掉的英雄不是排列而是组合？我也不太清楚，组合的话就可以过样例
        ll res = d[100][(1<<5)-1] * C(95, 5) % mod * A(90, 5) % mod *C(85, 5) % mod;
        printf("%lld\n", res);
    }
    return 0;
}

K - LOVER II

计蒜客 - A1617

solved by lwq

先给 a 从小到大排序，要让所有女生都有人与之配对，那么在最终的选择序列中，最少需要有 1 个男生与 \(a[1]\) 的和大于等于 k，有 \(2\) 个男生 与 \(a[2]\) 的 和大于等于 k，以此类推。所以初始化一个长度为 n 的数组，值为 \(-1,-2,-3,\cdots -n\)

然后对于 b 数组的每个位置 \(l\)， 找到最小的 \(r\)， 使得\([l,r]\) 之间的男生可以满足上面的条件，可以发现 \(r\) 随 \(l\) 递增而递增，所以每次可以用\(O(\log n)\)的时间插入一个元素，总共花费\(O(n\log n)\) 的时间预处理出来 r 数组，然后\(O(1)\) 回答询问即可

const int N = 200000 + 5;
int T, n, m, k, q, l, r;
int a[N], b[N], R[N];
struct SegTree{
    int l, r;
    int mi, lazy;
}t[N<<2];
void build(int p, int l, int r){
    t[p].l = l, t[p].r = r;
    t[p].lazy = 0;
    if(l == r){
        t[p].mi = -l;
        return;
    }
    int mid = l + r >> 1;
    build(p*2, l, mid);
    build(p*2+1, mid+1, r);
    t[p].mi = min(t[p*2].mi, t[p*2+1].mi);
}
void pushdown(int p){
    if(t[p].lazy){
        t[p*2].mi += t[p].lazy;
        t[p*2+1].mi += t[p].lazy;
        t[p*2].lazy += t[p].lazy;
        t[p*2+1].lazy += t[p].lazy;
        t[p].lazy = 0;
    }
}
void change(int p, int l, int r, int val){
    if(t[p].l >= l && t[p].r <= r){
        t[p].mi += val;
        t[p].lazy += val;
        return;
    }
    pushdown(p);
    int mid = t[p].l + t[p].r >> 1;
    if(mid >= l) change(p*2, l, r, val);
    if(mid < r) change(p*2+1, l, r, val);
    t[p].mi = min(t[p*2].mi, t[p*2+1].mi);
}
int main(){
    scanf("%d", &T);
    while(T--){
        scanf("%d%d%d", &n,&m, &k);
        for(int i=1;i<=n;i++)scanf("%d", &a[i]);
        for(int i=1;i<=m;i++)scanf("%d", &b[i]);
        sort(a + 1, a + 1 + n);
        build(1, 1, n);
        for(int i=1;i<=m;i++){
            R[i] = R[i-1];
            while(t[1].mi < 0){
                R[i] ++;
                if(R[i] > m) break;
                int pos = lower_bound(a + 1, a + 1 + n, k - b[R[i]]) - a;
                if(pos <= n){
                    change(1, pos, n, 1);
                }
            }
            int pos = lower_bound(a + 1, a + 1 + n, k - b[i]) - a;
            if(pos <= n);
            change(1, pos, n, -1);
        }
        scanf("%d", &q);
        while(q--){
            scanf("%d%d", &l, &r);
            if(R[l] > m ||  r < R[l]){
                puts("0");
            }else{
                puts("1");
            }
        }
    }
    return 0;
}