《深入理解计算机系统》实验一 —Data Lab

本文是CSAPP第二章的配套实验，通过使用有限的运算符来实现正数，负数，浮点数的位级表示。通过完成这13个函数，可以使我们更好的理解计算机中数据的编码方式。

准备工作

  首先去官网Lab Assignments获得实验相关的文件（也可以加我QQ获取教学视频、PPT等内容）在每个实验文件的README中都详细介绍了如何修改程序，编译程序等。建议仔细阅读，有不明白的可以留言，看到后会及时回复。

  我的编译环境：Ubuntu 16.04，gcc 5.4.0。

  编译时会报如下错误。

  执行以下命令，安装64位包。

sudo apt-get purge libc6-dev
sudo apt-get install libc6-dev
sudo apt-get install libc6-dev-i386

  再次编译，没有报错，正常。

题目

bitXor

思路

  德摩根律，也叫反演。

代码

/*
 * bitXor - x^y using only ~ and &
 *   Example: bitXor(4, 5) = 1
 *   Legal ops: ~ &
 *   Max ops: 14
 *   Rating: 1
 */
int bitXor(int x, int y) {
 return ~(x & y) & ~(~x & ~y);
}

tmin

思路

  补码的最小值0x80000000

代码

/*
 * tmin - return minimum two's complement integer
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 4
 *   Rating: 1
 */
int tmin(void) {
  return 1<<31;
}

isTmax

思路

  判断是否是补码的最大值。32位补码的最大值为0x7fffffff，与其异或，

代码

/*
 * isTmax - returns 1 if x is the maximum, two's complement number,
 *     and 0 otherwise
 *   Legal ops: ! ~ & ^ | +
 *   Max ops: 10
 *   Rating: 2
 */
int isTmax(int x) {
  return !(x^0x7fffffff);
}

allOddBits

思路

  这个题目还是比较简单的，采用掩码方式解决。首先要构造掩码，使用移位运算符构造出奇数位全1的数 mask ，然后获取输入x 值的奇数位，其他位清零（mask&x），然后与 mask进行异或操作，若相同则最终结果为0，然后返回其值的逻辑非。

代码

/* 方法一
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  int mask = 0xAA+(0xAA<<8);
  mask=mask+(mask<<16);
  return !((mask&x)^mask);
}

/* 方法二
 * allOddBits - return 1 if all odd-numbered bits in word set to 1
 *   Examples allOddBits(0xFFFFFFFD) = 0, allOddBits(0xAAAAAAAA) = 1
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 2
 */
int allOddBits(int x) {
  return !(~x&0xaaaaaaaa);
}

negate

思路

  补码实际上是一个阿贝尔群,对于x，-x是其补码，所以-x可以通过对x取反加1得到

代码

/*
 * negate - return -x
 *   Example: negate(1) = -1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 5
 *   Rating: 2
 */
int negate(int x) {
  return ~x+1;
}

isAsciiDigit

思路

  x分别与'0'和‘9’作差 ，然后根据作差的结果判断符号位的为0还是1即可

代码

/*

 * isAsciiDigit -return 1 if 0x30 <= x <= 0x39 (ASCII codes for characters '0' to '9')

 *   Example: isAsciiDigit(0x35) = 1.

 *            isAsciiDigit(0x3a) = 0.

 *            isAsciiDigit(0x05) = 0.

 *   Legal ops: ! ~ & ^ | + << >>

 *   Max ops: 15

 *   Rating: 3

 */

int isAsciiDigit(int x) {

  return(!((x+~48+1)>>31))&!!((x+~58+1)>>31);

}

conditional

思路

  把x转换为全0或者全1。这里注意下，0的补码是0，位表示全0。1的补码是-1，位表示全1。当x转为全0和全1时，再(x&y)或者(~x&z)时，一定有一个成立。返回的就是y或者z的值

代码

/*
 * conditional - same as x ? y : z
 *   Example: conditional(3,4,5) = 4
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 16
 *   Rating: 3
 */
int conditional(int x, int y, int z) {
  x = !!x;
  x = ~x+1;//求补码
  return (x&y)|(~x&z);
}

isLessOrEqual

思路

  通过位运算实现比较两个数的大小，无非两种情况：一是符号不同正数为大，二是符号相同看差值符号。

代码

/*
 * isLessOrEqual - if x <= y  then return 1, else return 0
 *   Example: isLessOrEqual(4,5) = 1.
 *   Legal ops: ! ~ & ^ | + << >>
 *   Max ops: 24
 *   Rating: 3
 */
int isLessOrEqual(int x, int y) {
  int negX=~x+1;//-x
  int addX=negX+y;//y-x
  int checkSign = addX>>31&1; //y-x的符号
  int leftBit = 1<<31;//最大位为1的32位有符号数
  int xLeft = x&leftBit;//x的符号
  int yLeft = y&leftBit;//y的符号
  int bitXor = xLeft ^ yLeft;//x和y符号相同标志位，相同为0不同为1
  bitXor = (bitXor>>31)&1;//符号相同标志位格式化为0或1
  return ((!bitXor)&(!checkSign))|(bitXor&(xLeft>>31));//返回1有两种情况：符号相同标志位为0（相同）位与 y-x 的符号为0（y-x>=0）结果为1；符号相同标志位为1（不同）位与x的符号位为1（x<0）
}

logicalNeg

思路

  逻辑非就是非0为1，非非0为0。利用其补码（取反加一）的性质，除了0和最小数(符号位为1，其余为0)，外其他数都是互为相反数关系（符号位取位或为1）。0和最小数的补码是本身，不过0的符号位与其补码符号位位或为0，最小数的为1。利用这一点得到解决方法。

代码

/*
 * logicalNeg - implement the ! operator, using all of
 *              the legal operators except !
 *   Examples: logicalNeg(3) = 0, logicalNeg(0) = 1
 *   Legal ops: ~ & ^ | + << >>
 *   Max ops: 12
 *   Rating: 4
 */

int logicalNeg(int x) {
  return ((x|(~x+1))>>31)+1;
}

howManyBits

思路

  正数的补码：正数最高位的1为第n个数，再加上符号位，结果为n+1。

  负数的补码：转换为正数，同上。

/* howManyBits - return the minimum number of bits required to represent x in
 *             two's complement
 *  Examples: howManyBits(12) = 5
 *            howManyBits(298) = 10
 *            howManyBits(-5) = 4
 *            howManyBits(0)  = 1
 *            howManyBits(-1) = 1
 *            howManyBits(0x80000000) = 32
 *  Legal ops: ! ~ & ^ | + << >>
 *  Max ops: 90
 *  Rating: 4
 */
int howManyBits(int x) {
  int b16,b8,b4,b2,b1,b0;
  int mask = x >> 31;
  x = (mask & ~x) | (~mask & x); //如果为正数，保持不变；如果为负数，按位取反

  //step1:判断高16为是否有1
  b16 = !!(x >> 16) << 4; //如果高16为有1,则b16 = 16，否则为0
  x >>= b16; //如果高16为有1,x右移16位舍弃低16位,在新的低16位继续查找；否则保持不变
  //step2:判断高8位是否有1
  b8 = !!(x >> 8) << 3;
  x >>= b8;
  //step3:高4位
  b4 = !!(x >> 4) << 2;
  x >>= b4;
  //step4:高2位
  b2 = !!(x >> 2) << 1;
  x >>= b2;
  //step5:高1位
  b1 = !!(x >> 1);
  x >>= b1;
  //step6:低1位
  b0 = x;

  return b16 + b8 + b4 + b2 + b1 + b0 + 1;
}

floatScale2

思路

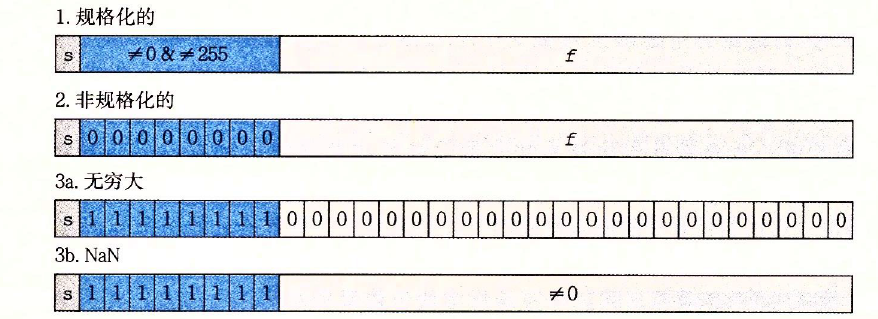
  参考上图理解下。不理解的回去看下IEEE标准浮点数格式《深入理解计算机系统》（CSAPP）读书笔记 —— 第二章 信息的表示和处理

  主要根据输入的数值，可以分为三种情况：

  1.输入uf为无穷大和NaN，直接返回uf

  2.uf为0或无穷小，返回2* uf + sign

  3.若exp+1 == 255，返回无穷大，否则 返回 exp+1。（exp为浮点数编码的整数部分，exp+1相当于uf * 2。）

代码

/*
 * floatScale2 - Return bit-level equivalent of expression 2*f for
 *   floating point argument f.
 *   Both the argument and result are passed as unsigned int's, but
 *   they are to be interpreted as the bit-level representation of
 *   single-precision floating point values.
 *   When argument is NaN, return argument
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
unsigned floatScale2(unsigned uf) {
  int exp = (uf&0x7f800000)>>23;//取出exp部分
  int sign = uf&(1<<31);//取出符号位
  if(exp==0) return uf<<1|sign;//情况2
  if(exp==255) return uf;//情况1
  exp++;
  if(exp==255) return 0x7f800000|sign;//情况3
  return (exp<<23)|(uf&0x807fffff);
}

floatFloat2Int

思路

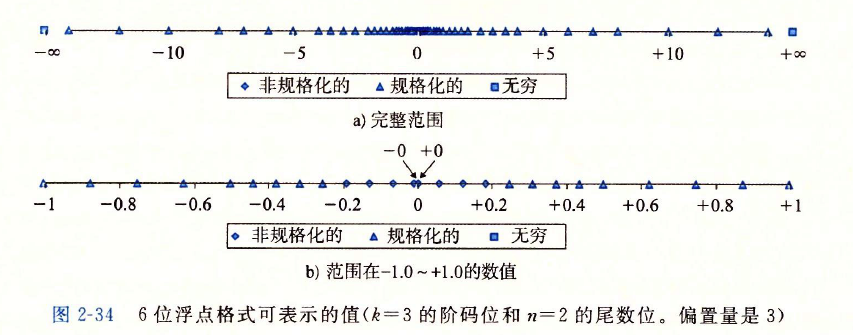
  1.非规格化，表示非常接近0的数，转换为int值后为0

  2.规格化，数的分布从接近0到无穷越来越稀疏，当f不超过int型表示的范围时，转换为int；当超过int型表示的范围时返回0x80000000u

  3.特殊，返回0x8000000u

  在规格化的float转换为int型整数时，

  如果E >= 31，小数点右移31位，此时隐含的1和frac占32位，另外还需要一个符号位，超出了int型范围

  如果E < 0，小数点左移1位后为0.1frac，转换为int后为0

  如果0 < E < 23, 小数点左移E为后需要舍弃frac中部分位，此时直接将frac右移23-E位，抹去小数部分

  如果23 <= E < 31，此时小数点右移后frac全部移到小数点以左，将frac左移E-23位，在后面补零

代码

/*
 * floatFloat2Int - Return bit-level equivalent of expression (int) f
 *   for floating point argument f.
 *   Argument is passed as unsigned int, but
 *   it is to be interpreted as the bit-level representation of a
 *   single-precision floating point value.
 *   Anything out of range (including NaN and infinity) should return
 *   0x80000000u.
 *   Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
 *   Max ops: 30
 *   Rating: 4
 */
int floatFloat2Int(unsigned uf) {
  int sign = (uf >> 31) & 1;
  int exp = (uf >> 23) & 0xff;
  int frac = uf & 0x7fffff;

  int E = exp - 127;

  if (E < 0) //小数
  {
    return 0;
  }
  else if (E >= 31) // 超出int范围
  {
    return 0x80000000u;
  }
  else
  {
    frac = frac | (1 << 23);  //加上隐含的1

    if (E < 23)     //舍去部分小数
    {
      frac >>= (23 - E);
    }
    else        //不需要舍去小数
    {
      frac <<= (E - 23);
    }

    if (sign)
      return -frac;
    else
      return frac;
  }
}

floatPower2

思路

根据浮点数求值公式：\(V = {( - 1)^s} \times M \times {2^E}\)

1.规格化

令M=1(frac = 0)，xEexp-Bias，exp=x+Bias

2.非规格化

exp = 0，在frac中令某一位为1，从而可使x更小。

	exp	frac	M	maxE	MinE
非规格化	0	0 * 10 *	0.frac	-127	-148
规格化	非0	0	1.0	127	-126

对边界情况分析

1.非规格化

• 当frac = 100 0000 0000 0000 0000 0000时，M = 0.1b = 0.5, E = 1- Bias = -126，此时v = 0.5 * 2.0 ^ -126 = 2.0 ^ -127
• 当frac = 000 0000 0000 0000 0000 0001时，M = 0.000 0000 0000 0000 0000 0001 = 2.0 ^ -22, E = -126，此时v = 2.0 ^ -22 * 2 ^ -126 = 2.0 ^ -148

2.规格化

• exp = 0xFF时，E = exp - Bias = 127
• exp = 1时，E = exp - Bias = -126

代码

unsigned floatPower2(int x) {
  if (x > 127) //too large, return +INF
  {
    return (0xFF << 23);
  }
  else if (x < -148) //too small, return 0
  {
    return 0;
  }
  else if (x >= -126) //norm，计算exp
  {
    int exp = x + 127;
    return (exp << 23);
  }
  else //denorm，令frac中某一位为1
  {
    int t = 148 + x;
    return (1 << t);
  }
}

测试结果

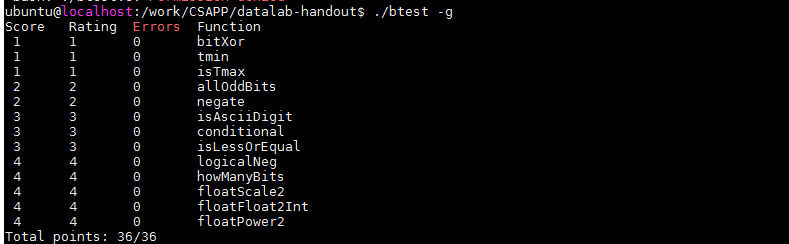
总结

  后面的几个题目还是很烧脑的，拿到题目不知所措，主要原因还是概念理解不到位。后来又去看书，理解了下基本概念，看了下其他人的解法，题目也可以慢慢理清楚了。解题过程代码也记录了下来，过段时间回来二刷可能会有新的解法。后面还有还几个实验等着我，慢慢来。欢迎关注我的博客及时获取更新通知。

  最后分享个PPT上看到的笑话，数绵羊~ 哈哈 ~



  养成习惯，先赞后看！如果觉得写的不错，欢迎关注，点赞，收藏，谢谢！

**如遇到排版错乱的问题，可以通过以下链接访问我的CSDN。

CSDN:CSDN搜索“嵌入式与Linux那些事”

欢迎欢迎关注我的公众号：嵌入式与Linux那些事，领取秋招笔试面试大礼包（华为小米等大厂面经，嵌入式知识点总结，笔试题目，简历模版等）和2000G学习资料。**