hdu5531 Rebuild

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)

Total Submission(s): 181    Accepted Submission(s): 42

Problem Description

Archaeologists find ruins of Ancient ACM Civilization, and they want to rebuild it.

The ruins form a closed path on an x-y plane, which has n endpoints.
The endpoints locate on (x1,y1), (x2,y2), …,(xn,yn) respectively.
Endpoint i and
endpointi−1 are
adjacent for 1<i≤n,
also endpoint 1 and
endpoint n are
adjacent. Distances between any two adjacent endpoints are positive integers.

To rebuild, they need to build one cylindrical pillar at each endpoint, the radius of the pillar of endpoint i is ri.
All the pillars perpendicular to the x-y plane, and the corresponding endpoint is on the centerline of it. We call two pillars are adjacent if and only if two corresponding endpoints are adjacent. For any two adjacent pillars, one must be tangent externally
to another, otherwise it will violate the aesthetics of Ancient ACM Civilization. If two pillars are not adjacent, then there are no constraints, even if they overlap each other.

Note that ri must
not be less than 0 since
we cannot build a pillar with negative radius and pillars with zero radius are acceptable since those kind of pillars still exist in their neighbors.

You are given the coordinates of n endpoints.
Your task is to find r1,r2,…,rn which
makes sum of base area of all pillars as minimum as possible.




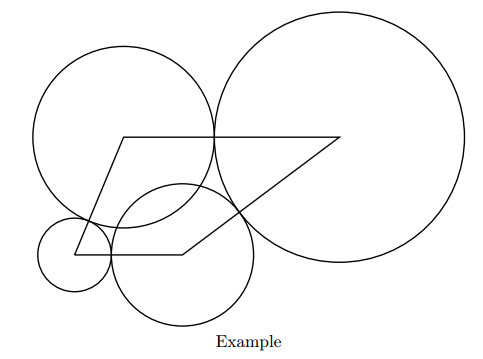
For example, if the endpoints are at (0,0), (11,0), (27,12), (5,12),
we can choose (r1, r2, r3, r4)=(3.75, 7.25, 12.75, 9.25).
The sum of base area equals to 3.752π+7.252π+12.752π+9.252π=988.816….
Note that we count the area of the overlapping parts multiple times.

If there are several possible to produce the minimum sum of base area, you may output any of them.

 

Input

The first line contains an integer t indicating
the total number of test cases. The following lines describe a test case.

The first line of each case contains one positive integer n,
the size of the closed path. Next n lines,
each line consists of two integers (xi,yi) indicate
the coordinate of the i-th
endpoint.

1≤t≤100
3≤n≤104
|xi|,|yi|≤104

Distances between any two adjacent endpoints are positive integers.

 

Output

If such answer doesn't exist, then print on a single line "IMPOSSIBLE" (without the quotes). Otherwise, in the first line print the minimum sum of base area, and then print n lines,
the i-th
of them should contain a number ri,
rounded to 2 digits after the decimal point.

If there are several possible ways to produce the minimum sum of base area, you may output any of them.

 

Sample Input

3
4
0 0
11 0
27 12
5 12
5
0 0
7 0
7 3
3 6
0 6
5
0 0
1 0
6 12
3 16
0 12

 

Sample Output

988.82
3.75
7.25
12.75
9.25
157.08
6.00
1.00
2.00
3.00
0.00
IMPOSSIBLE

 

这题卡了很久了，有点麻烦的题。给你一个多边形，问你能不能构造出圆心在多边形的顶点且各个圆相切，如果能，则求出所有圆的最大面积和。要分奇数和偶数讨论，奇数当一个圆的半径改变时，第一个圆和最后一个圆距离会变，偶数则不变。

#include<stdio.h>
#include<string.h>
#include<algorithm>
#include<math.h>
#include<iostream>
#include<stdlib.h>
#include<set>
#include<map>
#include<queue>
#include<vector>
#include<bitset>
#pragma comment(linker, "/STACK:1024000000,1024000000")
template <class T>
bool scanff(T &ret){ //Faster Input
    char c; int sgn; T bit=0.1;
    if(c=getchar(),c==EOF) return 0;
    while(c!='-'&&c!='.'&&(c<'0'||c>'9')) c=getchar();
    sgn=(c=='-')?-1:1;
    ret=(c=='-')?0:(c-'0');
    while(c=getchar(),c>='0'&&c<='9') ret=ret*10+(c-'0');
    if(c==' '||c=='\n'){ ret*=sgn; return 1; }
    while(c=getchar(),c>='0'&&c<='9') ret+=(c-'0')*bit,bit/=10;
    ret*=sgn;
    return 1;
}
#define inf 1073741823
#define llinf 4611686018427387903LL
#define PI acos(-1.0)
#define lth (th<<1)
#define rth (th<<1|1)
#define rep(i,a,b) for(int i=int(a);i<=int(b);i++)
#define drep(i,a,b) for(int i=int(a);i>=int(b);i--)
#define gson(i,root) for(int i=ptx[root];~i;i=ed[i].next)
#define tdata int testnum;scanff(testnum);for(int cas=1;cas<=testnum;cas++)
#define mem(x,val) memset(x,val,sizeof(x))
#define mkp(a,b) make_pair(a,b)
#define findx(x) lower_bound(b+1,b+1+bn,x)-b
#define pb(x) push_back(x)
using namespace std;
typedef long long ll;
typedef pair<int,int> pii;
#define NN 100100

struct node{
    double x,y;
}a[NN];

int n;
double len[NN];
double r[NN];
double caldis(int x,int y){
    return sqrt((a[x].x-a[y].x)*(a[x].x-a[y].x)+(a[x].y-a[y].y)*(a[x].y-a[y].y));
}
double cal(int idx,double lx){
    double temp=lx;
    double s=0.0;
    rep(i,1,n){
        s+=lx*lx;
        r[idx]=lx;
        if(lx<0.0||lx>len[idx]||lx>len[idx==1?n:idx-1])return -1.0;
        lx=len[idx]-lx;
        idx++;
        if(idx>n)idx=1;
    }
    if(fabs(temp-lx)>1e-7)return -1.0;
    return s;
}
int main(){
    tdata{
        scanff(n);
        rep(i,1,n){
            scanf("%lf%lf",&a[i].x,&a[i].y);
        }
        rep(i,1,n){
            if(i!=n)len[i]=caldis(i,i+1);
            else len[i]=caldis(i,1);
        }
        int idx;
        if(n&1){
            double lenx=0.0;
            idx=1;
            rep(i,1,n){
                if(i&1)lenx+=len[idx];
                else lenx-=len[idx];
                idx++;
                if(idx>n)idx=1;
            }
            lenx/=2.0;
            double ans=cal(1,lenx);
            if(ans>=0.0){
                printf("%.2f\n",ans*PI);
                rep(i,1,n){
                    printf("%.2f\n",r[i]);
                }
            }
            else printf("IMPOSSIBLE\n");
        }
        else{

            double lx=0.0,rx=len[1],t=0.0;
            idx=1;
            rep(i,1,n){
                t=len[idx]-t;
                if(i&1)rx=min(rx,t);
                else lx=max(lx,-t);
                idx++;
                if(idx>n)idx=1;
            }
            if(lx>rx){
                printf("IMPOSSIBLE\n");
                continue;
            }
            rep(i,1,250){
                /*
                double d=(rx-lx)/3.0;
                double d1=lx+d;
                double d2=rx-d;
                */
                double d1=(lx*2+rx)/3.0;
                double d2=(lx+rx*2)/3.0;
                if(cal(1,d1)<cal(1,d2))rx=d2;
                else lx=d1;
            }
            double ans=cal(1,lx);
            if(ans<0.0){
                printf("IMPOSSIBLE\n");
                continue;
            }
            printf("%.2f\n",ans*PI);
            rep(i,1,n){
                printf("%.2f\n",r[i]);
            }
        }
    }
    return 0;
}