Codeforces Round #654 (Div. 2)

比赛链接：https://codeforces.com/contest/1371

A. Magical Sticks

题意

有 $n$ 根小棍，长度从 $1$ 到 $n$，每次可以将两根小棍连接起来，问最多有多少根小棍长度相同。

题解

如：1 2 3 4 5，相同长度最多的情况为 1+4  2+3  5 。

即 $(1 + n - 1), (2 + n - 2), \dots$，所以答案为 $\lfloor \frac{n - 1}{2} \rfloor + 1$ 。

代码

#include <bits/stdc++.h>
using namespace std;

void solve() {
    int n; cin >> n;
    cout << (n - 1) / 2 + 1 << "\n";
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

B. Magical Calendar

题意

日历的一行为一周，问当一周的天数从 $1$ 到 $r$ 时，连续涂 $n$ 天的形状共有多少种。

题解

当 $r_i < n$ 时，连续涂 $n$ 天的形状共有 $r_i$ 种，因为第一天可以从 $r_i$ 个点开始涂，且形状都不相同；

当 $r_i \ge n$ 时，此时无论从哪一天开始涂，形状都是一条长方形。

所以：

• 若 $r<n$，答案即 $1+2+ \dots + r = \frac{r(r+1)}{2}$
• 若 $r \ge n$，答案即 $1+2+ \dots + (n - 1) + 1 = \frac{n(n-1)}{2} + 1$

代码

#include <bits/stdc++.h>
using ll = long long;
using namespace std;

void solve() {
    ll n, r; cin >> n >> r;
    cout << (r < n ? r * (r + 1) / 2 : n * (n - 1) / 2 + 1) << "\n";
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

C. A Cookie for You

题意

有 $a$ 个香草饼干，$b$ 个巧克力饼干，第一种客人有 $n$ 个，第二种客人有 $m$ 个。

第一种客人行动如下：如果香草饼干的个数多于巧克力饼干，吃一个香草饼干，否则吃一个巧克力饼干。

第二种客人行动如下：如果香草饼干的个数多于巧克力饼干，吃一个巧克力饼干，否则吃一个香草饼干。

如果一个客人要吃的饼干没有了，他就会生气，判断是否存在一种使所有客人都不会生气的方案。

题解

简化一下两种客人的行动：

第二种客人每次都会吃最少的一种饼干，一定会使两种饼干中的最小值发生变化，所以第二种客人吃的饼干数不会多于初始时两种饼干中的最小值。

第一种客人可以视为哪个多吃哪个，不一定会使两种饼干的最小值发生变化，所以应先让第二种客人吃最少的一种饼干，余下的饼干总数不少于第一种客人的个数就可以了。

代码

#include <bits/stdc++.h>
using ll = long long;
using namespace std;

void solve() {
    ll a, b, n, m; cin >> a >> b >> n >> m;
    cout << (a + b >= n + m and min(a, b) >= m ? "Yes" : "No") << "\n";
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}

D. Grid-00100

题意

向 $n \times n$ 的空方阵中填入 $k$ 个 $1$，使得每行、列 $1$ 的个数的最值差最小。

题解

首先最容易想到的是先按中央斜对角线填：

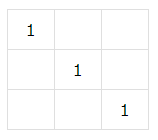
但是斜对角线长度不一，接下来就会变成这样：

此时第 $6$ 个 $1$ 显然填右上角最合适，即：

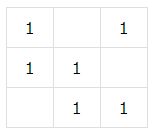
由此猜测从中央左下方和右上角依次填对角线。

值得一提的是，如果将左下角的对角线和右上角对应的对角线连起来，长度和中央对角线是相同的，同为 $n$，由此有了下面的简化写法。

代码

#include <bits/stdc++.h>
using namespace std;

void solve() {
    int n, k; cin >> n >> k;
    cout << (k % n == 0 ? 0 : 2) << "\n";
    int MP[n][n] = {};
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            if (k > 0) {
                MP[j][(i + j) % n] = 1;
                --k;
            }
    for (int i = 0; i < n; i++) {
        for (int j = 0; j < n; j++)
            cout << MP[i][j];
        cout << "\n";
    }
}

int main() {
    int t; cin >> t;
    while (t--) solve();
}