中心极限定理（为什么y服从高斯分布）

因为每一条数据都服从IID原则：

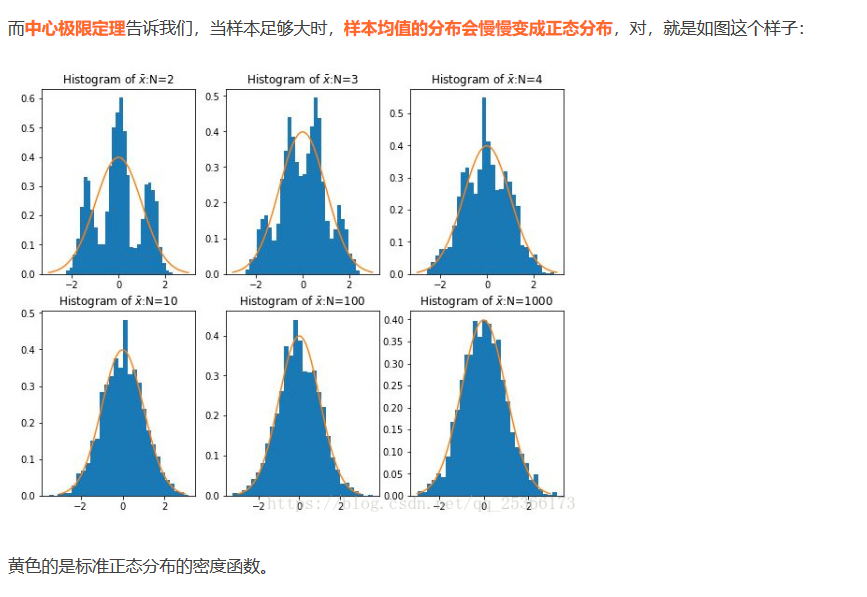
根据中心极限定理，当数据增加的时候，样本均值的分布慢慢变成正态分布

不管分布式什么分布，累加起来都是高斯分布

As sum increases, sum of non-Gaussian, finite variance variables is also Gaussian

为什么要累加？因为Y出现的概率等于n个小y出现的概率相乘

p(Y)=累加p(yi)

In probability theory, the central limit theorem (CLT) establishes that, in some situations, when independent random variables are added, their properly normalized sum tends toward a normal distribution