LeetCode-P53题解【动态规划】

本文为原创，转载请注明：http://www.cnblogs.com/kylewilson/

题目出处：

https://leetcode.com/problems/maximum-subarray/description

题目描述：

找出连续子区间最大和，至少包含一个数

例如：[-2,1,-3,4,-1,2,1,-5,4]，则子区间[4,-1,2,1]有最大和为6

输入：

[-2,1,-3,4,-1,2,1,-5,4]

思路分析：

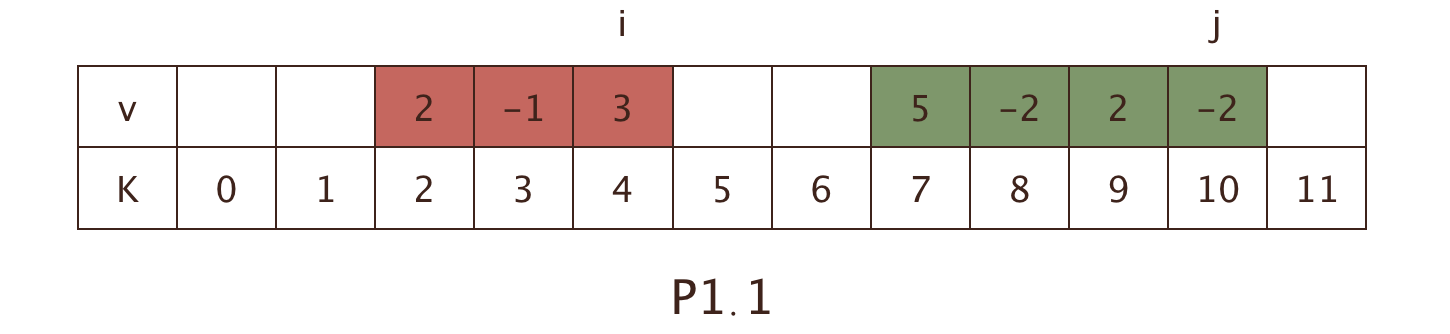
解法一：

如上图P1.1：

最优解一定为一段连续的区间，则可以有O(n*n)的解法，即遍历所有的区间找出最大值

设sum[i]为区间[1,i]的和，初始化处理

最优解=max(sum[i]-sum[j]), (0<=i,j<n)

解法二：

假设最大区间和为上图红色区域，可以看出，点i一定是该区间最右边节点；

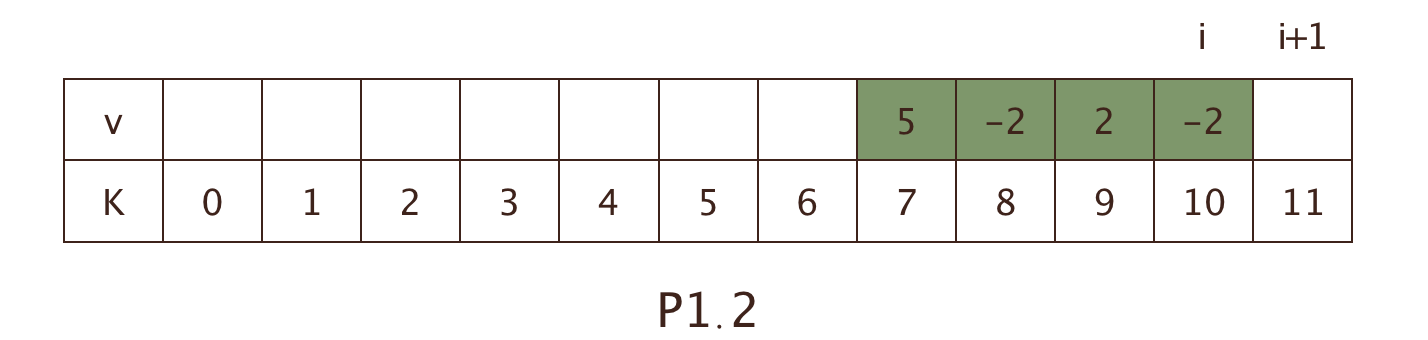
图P1.2

设f[i]为以i结尾的最大连续区间和

为什么一定要以i结尾？

因为f[i]为一维数组，不加这个条件，则f[i]无法表示出前面的状态，只知道前i个节点的最优解，但不知道最优解从哪里开始

如果已经求出i个节点的最大区间和，则增加一个节点i+1时，前i+1个节点的最优解只有两种情况

1）i+1不在最优解区间中，这种情况和只有i个节点是一样的

2）i+1在最优解区间中， 这和情况i+1一定是最优解的最右边节点，又分两种情况

　　2-1) 前i个节点的最优解为负数，则舍弃前面的和，因为加上前面的和会更小

　　f[i+1]=f[i]+line[i+1]

　　2-2) 前i个节点的最优解为正数，则加上前面的和，因为加上前面的和会更大

　　f[i+1]=line[i+1]

最优解=max(f[i]), (0<=i<n)

注：每一个节点i只与之前的一个节点i-1相关，所以用滚动变量，空间复杂度为O(1)

C++源码如下：

github: https://github.com/Kyle-Wilson1/Leetcode/tree/master/P53

class Solution {
public:

    Solution() = default;

    static int maxOfTwo(int a, int b) {
        return a > b ? a : b;
    }

    int maxSubArray(vector<int> &nums) {
        int pre = 0, now = 0, maxAnswer = -2147483647;
        for (int num : nums) {

            if (pre > 0)
                now = pre + num;
            else
                now = num;
            maxAnswer = maxOfTwo(maxAnswer, now);
            pre = now;
        }
        return maxAnswer;
    }
};