实现图像上像素点与实际位置的GPS对应

作者有话说

这篇随笔是基于我自己完成的一个项目，这个项目虽然看起来较为简单，但是由于我本身不是学这个方向的，因此在做的过程中还是遇到了一些大大小小的问题。经过仔细研究并多次调试代码，终于把这个问题的原理弄懂了。下面我将详细介绍该问题的解决过程，并在随笔末尾附上所有相关代码，希望有兴趣的可以一起交流学习。

目录

• 问题介绍
• 相关专业术语介绍
• 解决思路及过程
• 一些值得注意的细节
• 结果
• 参考文献
• MATLAB代码

问题介绍  

无人机的出现给拍照录像带来了极大的便利。如下图所示，无人机停留在高为2m的高空中，其所装配的相机的拍摄方向与垂直方向的夹角为60°，利用相机参数求解所拍摄图像上所有像素点的大地坐标，实现图像上所有像素点与实际位置的GPS对应。另外，相机拍摄时的经纬度为（118.8675992，32.032575），相机的焦距为16mm，成像像素长和宽分别为4.65µm和3.9µm。

相关名词介绍

• 焦距：焦距指镜头等效光心到相机传感器的距离。
• 大地坐标：大地测量中以参考椭球面（本文是以地球表面）为基准面的坐标。地面点P的位置用大地经度L、大地纬度B和大地高H表示。当点在参考椭球面上时，仅用大地经度和大地纬度表示。大地经度是通过该点的大地子午面与起始大地子午面之间的夹角，大地纬度是通过该点的法线与赤道面的夹角，大地高是地面点沿法线到参考椭球面的距离。
• 高斯平面坐标系：指的是以中央子午线与赤道的交点作为坐标原点，以中央子午线的投影为纵坐标轴X，规定X轴向北为正，以赤道的投影为横坐标轴Y，Y轴向东为正，形成的坐标系。

解决思路及过程

考虑到地球是椭球形状的，而经纬度是大地坐标，不方便计算，所以先利用高斯投影正算公式将大地平面坐标转换为高斯平面坐标，高斯平面坐标又和高度构成一个三维空间坐标。根据相机成像原理，把像素正中心坐标作为一个空间坐标，把相机中心坐标作为一个空间坐标，过这两点的直线与高斯平面的交点就是这个像素点所对应的实际位置。

• 具体步骤

1. 我们将相机所在地理位置的大地坐标通过高斯正变换转换成高斯平面坐标，高斯平面加上高度构成了三维空间，所以就实现了每个点都有一个三维坐标与其对应。
2. 我们根据焦距、相机中心的空间坐标、和角度确定出图像上每个像素点所对应的空间坐标。
3. 根据像素点坐标和相机中心坐标求出像素点所对应的实际位置高斯平面中的坐标。
4. 将步骤3得到的实际位置的高斯坐标通过高斯逆变换得到其对应的大地坐标。

• 图示说明

下图反映了由图片像素点得到对应实际位置的过程，考虑到成像屏的尺寸相对于拍摄的实物来说非常小，所以我们把这两部分分开画图。图1和图2结合起来表示由像素点对应到实际位置的原理，即过像素点（彩色方格）与相机中心（空心圆点）的射线（彩线）与高斯平面的交点即为像素点对应的实际位置（射线终点）。

图1  光线从相机中心到像素点示意图

图2  光线从实际位置到相机中心示意图（斜视）

图3  光线从实际位置到相机中心示意图（俯视）

• 高斯投影说明

1. 高斯投影正算公式
2. 高斯投影反算公式

1.已知大地坐标$\left ( B,L \right )$及中央子午线经度$L_{0}$，计算高斯平面坐标$\left ( x,y \right )$，公式如下：

$ x=X+\frac{N}{2}sin\left ( B \right )cos\left ( B \right )l^{2}+\frac{N}{24}sin\left ( B \right )cos^{3}\left ( B \right )\left ( 5-t^{2}+9\eta ^{2}+4\eta ^{4} \right )l^{4}+\frac{N}{720}sin\left ( B \right )cos^{5}\left ( B \right )( 61-58t^{4}+270\eta ^{2}-330\eta ^{2}t^{2})l^{6}$

$y=Ncos\left ( B \right )l+\frac{N}{6}cos^{3}\left ( B \right )\left ( 1-t^{2}+\eta ^{2} \right )l^{3}+\frac{N}{120}cos^{5}\left ( B \right )\left ( 5-18t^{2}+t^{4}+14\eta ^{2}-58\eta ^{2}t^{2} \right )l^{5}$

其中，$B$为纬度，$l=L-L_{0}$，单位为弧度，$N=\frac{a}{\sqrt{1-e^{2}sin^{2}\left ( B \right )}}$，为卯酉圈曲率半径，$t=tan\left ( B \right )$，$\eta ^{2}=e^{2}cos^{2}\left ( B \right )$，$e=\frac{\sqrt{a^{2}-b^{2}}}{b}$为第二偏心率，$a$为旋转椭球长半轴，$b$为短半轴，$X$为子午线弧长。

2.已知高斯平面坐标$\left (x,y  \right )$及指定中央子午线经度$L_{0}$，计算大地坐标$\left ( B,L \right )$:

$B=B_{f}-\frac{t_{f}}{2M_{f}N_{f}}y^{2}+\frac{t_{f}}{24M_{f}N_{f}^{3}}\left (5+3t_{f}^{2}+\eta _{f}^{2}-9t_{f}^{2}\eta _{f}^{2}  \right )y^{4}+\frac{t_{f}}{720M_{f}N_{f}^{5}}\left ( 61+90t_{f}^{2}+45t_{f}^{4} \right )y^{6}$

$L=L_{0}+\frac{1}{N_{f}cos\left ( B_{f} \right )}y-\frac{1}{6N_{f}^{3}cos\left ( B_{f} \right )}\left ( 1+2t_{f}^{2}+\eta _{f}^{2} \right )y^{3}+\frac{1}{120N_{f}^{5}cos\left ( B_{f} \right )}\left ( 5+28t_{f}^{2}+24t_{f}^{4}+6\eta _{f}^{2}+8t_{f}^{2}\eta _{f}^{2} \right )y^{5}$

其中，$N_{f}=\frac{a}{\sqrt{1-e^{2}sin\left ( B_{f} \right )}}$，$M_{f}=\frac{a\left ( 1-e^{2} \right )}{\sqrt{\left (1-e^{2}sin\left ( B_{f} \right )  \right )^{3}}}$，$\eta _{f}^{2}=e^{2}cos^{2}\left ( B_{f} \right )$，$t_{f}=tan\left ( B_{f} \right )$，$B_{f}$为根据子午线弧长$X$反算的底点纬度。

一些值得注意的细节

保证一定的精度：因为像素尺寸非常小，他们所对应的实际位置的经纬度差别也是很小的，我刚处理的时候没有考虑到这个问题，所以导致得到的结果很多都是一样的（结果被截断了）。所以我后来将输出数据的位数设定为10为小数，才看出其差别。

结果

经过编程计算，我们把得到经纬度数据分别根据像素大小画出一张曲面来观察结果的合理性，如下图（图4、图5）所示：

                     

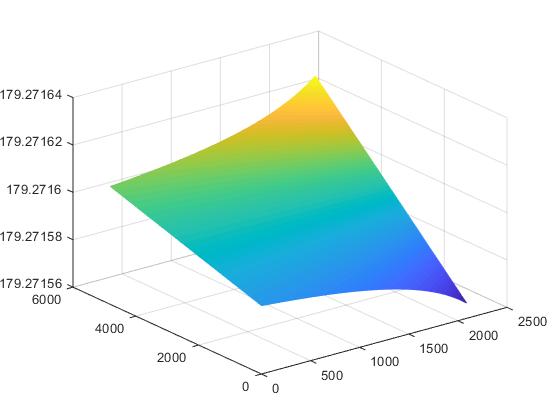
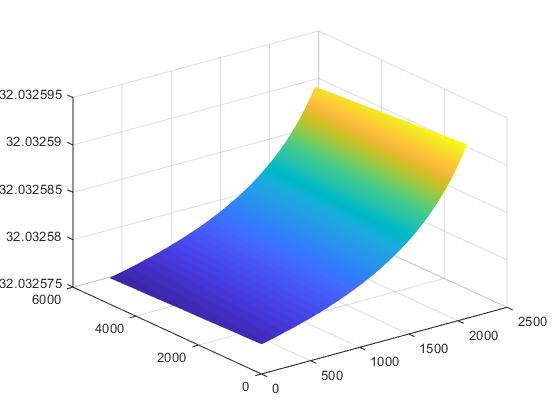
图4：经度                                         图5：纬度

根据图4和图5，可以看出经纬度变化的连续性和对称性，而且数值又徘徊在相机经纬度坐标周围，因此是合理的。

参考文献链接

matlab大地测量高斯投影正反算程序设计实验 - 百度文库https://wenku.baidu.com/view/121aedfdee06eff9aff807a3.html#

MATLAB代码

main.m

clear all;
clc;
tic
format long
jiaodu=(angle)/180*pi;
PixelLength=4.65/(10^6);
PixelWidth=3.9/(10^6);
ImageSize=[3376 6016];
U_0=ImageSize(1)/2;
V_0=ImageSize(2)/2;
a=6378137;%长半轴
f1=1/298.257223563;%扁率
b=a*(1-f1);%短半轴
e=(sqrt(a^2-b^2))/a;%第一偏心率
e_=(sqrt(a^2-b^2))/b;%第二偏心率
A=[120.2719052 33.1664600];
f=16/(10^3);
global c
c=num2str(floor(A(2)*1000));
c=str2num(c(end));
H=2;
X=latitude2meridian(dms2rad(A(:,2)),a,e);%X为子午线弧长，有纬度B算出
[x,y,L0]=GaussianMapDirect(dms2rad(A(:,2)),dms2degree(A(:,1)),X);
CameraCenter=[x,y,H];
TT=[cos(jiaodu) -sin(jiaodu);sin(jiaodu) cos(jiaodu)];
I=zeros(ImageSize(1),ImageSize(2)*3);
T=zeros(ImageSize(1),ImageSize(2)*2);
MeridianLongitude=L0;
for i=1:ImageSize(1)
    for j=1:ImageSize(2)
        I(i,(j-1)*3+1:j*3)=ImagePointCoordinates(ImageSize(1),ImageSize(2),i,j,PixelLength,PixelWidth,f,CameraCenter);
        P=I(i,(j-1)*3+1:j*3-1)-CameraCenter(1:2);
        P=P*TT;
        I(i,(j-1)*3+1:j*3-1)=P+CameraCenter(1:2);
        [T(i,(j-1)*2+1),T(i,j*2)]=ImagePointMapping(CameraCenter,I(i,(j-1)*3+1:j*3));
        [G(i,(j-1)*2+1),G(i,j*2)]=GaussianMapInverse(T(i,(j-1)*2+1),T(i,j*2),dms2rad(MeridianLongitude));
    end
end
for i=1:ImageSize(1)
    for j=1:1
       I(i,(j-1)*3+1:j*3)=ImagePointCoordinates(ImageSize(1),ImageSize(2),i,j,PixelLength,PixelWidth,f,CameraCenter);
        P=I(i,(j-1)*3+1:j*3-1)-CameraCenter(1:2);
        P=P*TT;
        I(i,(j-1)*3+1:j*3-1)=P+CameraCenter(1:2);
        [T(i,(j-1)*2+1),T(i,j*2)]=ImagePointMapping(CameraCenter,I(i,(j-1)*3+1:j*3));
        [G(i,(j-1)*2+1),G(i,j*2)]=GaussianMapInverse(T(i,(j-1)*2+1),T(i,j*2),dms2rad(MeridianLongitude));
    end
end
for i=2:ImageSize(1)
    for j=2:ImageSize(2)
        if j<=ImageSize(2)/2
            I(i,(j-1)*3+2)=I(1,(j-1)*3+2);
            I(i,(j-1)*3+1)=I(i,1);
            I(i,j*3)=I(i,3);
            T(i,(j-1)*2+1)=T(i,1);
            [T(i,(j-1)*2+1),T(i,j*2)]=ImagePointMapping(CameraCenter,I(i,(j-1)*3+1:j*3));
            [G(i,(j-1)*2+1),G(i,j*2)]=GaussianMapInverse(T(i,(j-1)*2+1),T(i,j*2),dms2rad(MeridianLongitude));
        else
            T(i,(j-1)*2+1)=T(i,1);
            T(i,j*2)=2*CameraCenter(2)-T(i,(ImageSize(2)+1-j)*2);
            [G(i,(j-1)*2+1),G(i,j*2)]=GaussianMapInverse(T(i,(j-1)*2+1),T(i,j*2),dms2rad(MeridianLongitude));
        end
    end
end

toc

GaussianTransformation.m

%首先读取文件data1 .txt中的数据，计算其在相应六度带高斯投影带内的高斯平面直角坐标，并存贮在文件data2.txt 中，
%datal.txt格式为:经度( dd.mmss) 纬度( dd.mmss) 大地高
%data2.txt格式为:x(m) y(m) 中央子午线经度(dd.mmss)
clear all;
clc;
[filename,pathname]=uigetfile('*.*');%文件查找窗口
file=fullfile(pathname,filename);%合并路径文件名.
A=importdata(file);%将生成的文件导入工作空间，变量名为A
%RefEllipsoid为椭球参数
%RefEllipsoid=[a,b,c,f,e2,e2_];
a=6378137;%WGS84椭球参数:长半轴
f=1/298.257223563;%扁率
b=a*(1-f);%WGS84椭球参数:短半轴
e=(sqrt(a^2-b^2))/a;
% [a b]=size(A.data);
% A1=[];
% for i=1:a
%     data1=A.data(i,:);
%     data1=data1(find(isnan(data1)==0));
%     A1=[A1;data1];
% end
% A.data=A1;
X=latitude2meridian(dms2rad(A.data(:,2)),a,e);%X为子午线弧长，有纬度B算出
[x,y,L0]=GaussianMapDirect(dms2rad(A.data(:,2)),dms2degree(A.data(:,1)),X);
B=[x,y,L0];
%B为重组矩阵
[filename_out,pathname_out]=uiputfile('*.txt','请输入文件名');
%文件查找窗口
fileout=fullfile(pathname_out,filename_out);
%合并路径文件名
fid=fopen(fileout,'wt');
%新建打开txt文件
fprintf(fid,'x(m) y(m) 中央子午线经度(dd.mms)\n');
[a b]=size(B);
for i=1:a
    fprintf(fid,'%f %f %f\n',B(i,:));
end
fclose(fid);

InverseGaussianTransform.m

%然后根据文件data2.txt中的高斯平面直角坐标及其中央子午线经度，计算其经纬度，并将计算结果按照格式存贮在文件data3.txt 中，
%data3.txt格式为:经度(dd.mmss) 纬度(dd.mmss)
clear all;
clc;
format long
[filename,pathname]=uigetfile('*.*');%文件查找窗口
file=fullfile(pathname,filename);%合并路径文件名
A=importdata(file);%将生成的文件导入工作空间，变量名为A
A.data(:,3)=177*ones(10051632,1);
[L,B]=GaussianMapInverse(A.data(:,1),A.data(:,2),dms2rad(A.data(:,3)));
C=[L,B];%C为重组矩阵
[filename_out,pathname_out]=uiputfile('*.txt','请输入文件名');
%文件查找窗口
fileout=fullfile(pathname_out,filename_out);%合并路径文件名
fid=fopen(fileout,'wt');%新建打开txt文件
fprintf(fid,'经度(dd.mmss) 纬度(dd.mmss)\n');
[a b]=size(C);
for i=1:a
    fprintf(fid,'%.10f %.10f\n',C(i,:));
end
fclose(fid);

degree2dms.m

function dms=degree2dms(du)
%度一>度分秒(ddmmss)
degree=fix(du);
min=fix((du-degree)*60);
second=(((du-degree)*60-min)*60);
dms=degree+min/100+second/10000;
end

dms2degree.m

function degree=dms2degree(jiaodu)
%度分秒(dd.mmss)->度
degree=fix(jiaodu);
mimute=fix((jiaodu-degree)*100);
second=(jiaodu-degree-mimute/100)*10000;
degree=degree+mimute/60+second/3600;
end

dms2rad.m

function rad=dms2rad(n)
deg=fix(n);%度取所给数n的整数部分
min_tem=(n-deg)*100;%去掉整数部分后小数点后移两位
min=fix(min_tem);%分取整
sec=(min_tem-min)*100;%秒是小数点再向后移两位的数字
rad=(deg+min/60.00+sec/3600)*pi/180.0;
end

GaussianMapDirect.m

function [x,y,L0]=GaussianMapDirect(B,L,X)
%WGS84椭球参数:
a=6378137;%长半轴
f=1/298.257223563;%扁率
b=a*(1-f);%短半轴
e=(sqrt(a^2-b^2))/a;%第一偏心率
e_=(sqrt(a^2-b^2))/b;%第二偏心率
%当地中央子午线决定于当地的直角坐标系统，首先确定您的直角坐标系统是3度带还是6度带投影，然后再根据如下公式推算。
Q=input('请选择投影带:\n');
if Q==6
    %6度带:
    M=round((L+3)./6);
    %带号M=round[(L+3)/6]，即对(L+3)/6的值四舍五入取整数，L为当地经度;
    L0=6.*M-3 ;
    %则中央子午线经度L0=6 X M-3
else
    %3度带:
    M=round(L./3);%带号M=round([L/3)，即对(L/3)的值四舍五入取整数，L为当地经度;
    L0=3.*M;
    %则中央子午线经度L0=3 X M
end
l=(L-L0).*pi/180;
N=a./(sqrt(1-(e^2).*(sin(B).^2)));
t=tan(B);
p=e_.*cos(B);%p表示yita
%计算高斯平面坐标(x，y)
x=X+(N.*(sin(B)).*(cos(B)).*(l.^2))./2+(N.*(sin(B)).*((cos(B)).^3).*(5-((t).^2)+9.*(p.^2)+4.*(p.^4)).*(l.^4))./24+(N.*sin(B).*(cos(B)).^5.*(61-58.*(t.^2)+(t.^4)+270.*(p.^2)-330.*(p.^2).*(t.^2)).*(l.^6))./720;
y=N.*cos(B).*l+(N.*(cos(B)).^3.*(1-t.^2+p.^2).*(l.^3))./6+(N.*((cos(B)).^5).*(5-18.*(t.^2)+t.^4+14.*(p.^2)-58.*(p.^2).*(t.^2)).*(l.^5))./120;
L0=degree2dms(L0);
end

GaussianMapInverse.m

function [L,B] = GaussianMapInverse(x,y,L0)
%WGS84椭球参数:
a=6378137;%长半轴
f=1/298.257223563; %扁率
b=a*(1-f);%短半轴
e=(sqrt(a^2-b^2))/a;%第- -偏心率
e_=(sqrt(a^2-b^2))/b;%第二偏心率
%根据中央子午线弧长x反算底点纬度Bf
Bf=meridian2latitude(x,a,e);
Nf=a./sqrt(1-(e.^2).*(sin(Bf).^2));
Mf=a.*(1-e.^2)./sqrt((1-(e.^2).*(sin(Bf).^2)).^3);
pf=e_.*cos(Bf);
tf=tan(Bf);
%已知高斯平面坐标(x, y)及指定中央子午线经度L0，计算大地坐标(B,L)
B=Bf-tf.*(y.^2)./(2.*Mf.*Nf)+tf.*(5+3.*(tf.^2)+pf.^2-9.*(tf.^2).*(pf.^2)).*(y.^4)./(24.*Mf.*(Nf.^3))+tf.*(61+90.*(tf.^2)+45.*(tf.^4)).*(y.^6)./(720.*Mf.*(Nf.^5));
L=L0+y./(Nf.*cos(Bf))-(1+2.*(tf.^2)+pf.^2).*y.^3./(6.*(Nf.^3).*cos(Bf))+(5+28.*tf.^2+24.*tf.^4+6.*pf.^2+8.*(tf.^2).*pf.^2).*y.^5./(120.*Nf.^5.*cos(Bf));
B=rad2dms(B);
L=rad2dms(L);
end

ImagePointCoordinates.m

function PixelCoordinates=ImagePointCoordinates(L,H,m,n,PixelLength,PixelWidth,focalLength,CameraCenter)
format long g
HH=H/2;
LL=L/2;
ImageCenter(1)=CameraCenter(1)-focalLength*sin(pi/3);
ImageCenter(2)=CameraCenter(2);
ImageCenter(3)=CameraCenter(3)+focalLength*sin(pi/3);
if m<=HH&&n<=LL
    PixelCoordinates(1)=ImageCenter(1)+((HH-m)*PixelWidth+0.5*PixelWidth)*sin(pi/6);
    PixelCoordinates(2)=ImageCenter(2)+(LL-n)*PixelLength+0.5*PixelLength;
    PixelCoordinates(3)=ImageCenter(3)+((HH-m)*PixelWidth+0.5*PixelWidth)*cos(pi/6);
end
if m<=HH&&n>LL
    PixelCoordinates(1)=ImageCenter(1)+((HH-m)*PixelWidth+0.5*PixelWidth)*sin(pi/6);
    PixelCoordinates(2)=ImageCenter(2)+(LL-n)*PixelLength-0.5*PixelLength;
    PixelCoordinates(3)=ImageCenter(3)+((HH-m)*PixelWidth+0.5*PixelWidth)*cos(pi/6);
end
if m>HH&&n<=LL
    PixelCoordinates(1)=ImageCenter(1)+((HH-m)*PixelWidth-0.5*PixelWidth)*sin(pi/6);
    PixelCoordinates(2)=ImageCenter(2)+(LL-n)*PixelLength+0.5*PixelLength;
    PixelCoordinates(3)=ImageCenter(3)+((HH-m)*PixelWidth-0.5*PixelWidth)*cos(pi/6);
end
if m>HH&&n>LL
    PixelCoordinates(1)=ImageCenter(1)+((HH-m)*PixelWidth-0.5*PixelWidth)*sin(pi/6);
    PixelCoordinates(2)=ImageCenter(2)+(LL-n)*PixelLength-0.5*PixelLength;
    PixelCoordinates(3)=ImageCenter(3)+((HH-m)*PixelWidth-0.5*PixelWidth)*cos(pi/6);
end

ImagePointMapping.m

function [x,y]=ImagePointMapping(CameraCenter,Point)
format long
x=-CameraCenter(3)/(CameraCenter(3)-Point(3))*(CameraCenter(1)-Point(1))+CameraCenter(1);
y=-CameraCenter(3)/(CameraCenter(3)-Point(3))*(CameraCenter(2)-Point(2))+CameraCenter(2);
end

latitude2meridian.m

function x=latitude2meridian(B,a,e)
%由纬度B求对应的子午线弧长x，计算公式
m0=a*(1-e^2);
m2=(3*(e^2)*m0)/2;
m4=(5*(e^2)*m2)/4;
m6=(7*(e^2)*m4)/6;
m8=(9*(e^2)*m6)/8;
a0=m0+m2/2+3*m4/8+5*m6/16+35*m8/128;
a2=m2/2+m4/2+15*m6/32+7*m8/16;
a4=m4/8+3*m6/16+7*m8/32;
a6=m6/32+m8/16;
a8=m8/128;
x=a0*B-(a2*sin(2*B))/2+(a4*sin(4*B))/4-(a6*sin(6*B))/6+(a8*sin(8*B))/8;
end

meridian2latitude.m

function B=meridian2latitude(x,a,e)
m0=a*(1-e^2);
m2=(3*(e^2)*m0)/2;
m4=(5*(e^2)*m2)/4;
m6=(7*(e^2)*m4)/6;
m8=(9*(e^2)*m6)/8;
a0=m0+m2/2+3*m4/8+5*m6/16+35*m8/128;
a2=m2/2+m4/2+15*m6/32+7*m8/16;
a4=m4/8+3*m6/16+7*m8/32;
a6=m6/32+m8/16;
a8=m8/128;
%%纬度B的计算
B0=x./a0;%B的初始值
while 1
    F=-(a2.*sin(2.*B0))./2+(a4.*sin(4.*B0))./4-(a6.*sin(6.*B0))./6+(a8.*sin(8.*B0))./8;
    B=(x-F)./a0;
    if abs(B0-B)<10^(-6)
        break;
    end
    abs(B0-B);
    B0=B;
end
end

rad2dms.m

function dms=rad2dms(azimuth)%弧度转度分秒
dgree_tem=azimuth*180/pi;
dgree=fix(dgree_tem);
min_tem=((dgree_tem-dgree)*60);
min=fix(min_tem);
second=((min_tem-min)*60);
dms=dgree+min/100+second/10000;
end