【换根DP】小奇的仓库

题目背景

小奇采的矿实在太多了，它准备在喵星系建个矿石仓库。令它无语的是，喵星系的货运飞船引擎还停留在上元时代！

题目内容

喵星系有$n$个星球，星球以及星球间的航线形成一棵树。

从星球$a$到星球$b$要花费$[\text{dis}(a,b)\ \text{xor}\ M]$秒。（$\text{dis}(a,b)$表示ab间的航线长度，$\text{xor}$为位运算中的异或）

为了给仓库选址，小奇想知道，星球$i(1\leq i\leq n)$到其它所有星球花费的时间之和。

数据范围

$6\leq n\leq 100000,0\leq M\leq 15$

思路

出题人：

算法1：

不会写函数的小伙伴们，我们只需要写个floyd，就有10分啦！

算法2：

在算法1的基础上，我们对每条边处理一下xor，就有20分啦！

算法3：

简单的树形DP，或者你会nlogn的dij，处理完每个点到其它点的最短路后再加上xor，那么这样就有30分啦！

算法4：

第4、5个点无需xor，那么我们树形DP扫一个节点与其它所有节点的路径长度之和，可以合并信息，最终均摊O(1)，50分到手。

算法5：

第6个点xor 1，那么我们树形DP到一个点时记录有多少个0，多少个1，然后每当一条路径到2，那部分就再记录一个值，60分到手。

算法6：

如果你第6个点都过了，却没有满分，笨死啦！

一样的嘛，就是原来的“0”、“1”、大于等于2变成了0~16么~~

满了。

我：？

考场上直接打的$O(n^2)$枚举区间再加上求$\text{LCA}$的复杂度的暴力，结果一时脑瘫建边的时候就异或了$M$结果惨挂$10pts$，然后考后改成最后再异或就$30pts$了...（差点有比郭神高的机会呢qwq）

然后正解是换根$dp$，又是假期埋下的一个坑吗

先考虑没有异或的情况。设已经搜到了边$<u,v,w>$，且$u$是$v$的父亲，那么如何更新$ans[v]$呢？

\[ans[v]=ans[u]+(n-size[v])\times w-size[v]\times w
\]

当然你会选择合并同类项，不过先不合并比较好理解，对于$u$以上的节点，其个数为$n-size[v]$，对于原来的$ans[u]$距离多了一个$w$，所以加上$(n-size[v])\times w$，对于$v$的子树节点，对$v$的距离就是其到$u$的距离减去$w$，所以就能得到以上的柿子。

大概这个样子：

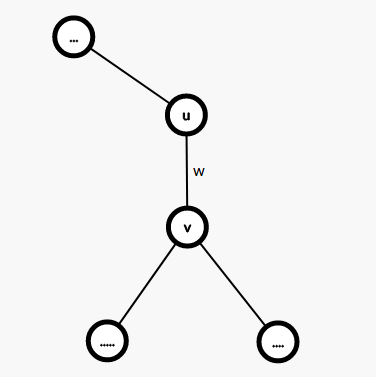
然而本题要求异或，由我惨挂10分的经历可以知道异或并不满足分配律，所以并不能边加边异或。然而可以看出$M\leq 15$，转换为二进制为$1111$，所以最后异或$M$的时候仅会对后四位有影响，所以只需要记录后四位的状态即可。

设$f[i][j]$表示到了$i$点，当前后四位的状态为$j$，能伸展出的路径条数。

对于初始：$f[u][0]=1$，表示自己到自己为一条路径。为了方便，你可以先加上自己然后最后减去。

然后就是$f[u][(j+w)\ \%\ 16]+=f[v][j]$，从子树转移过来。

然而除了子树以外还有别的点，如何转移呢？

\[f[v][(j+w)\ \%\ 16]+=(f[u][j]-f[v][(j-w)\ \%\ 16])
\]

很容易理解，对于$v$的父亲$u$，先刨去子树$v$的贡献，然后剩下的就是其他点到$u$的贡献，你再通过$<u,v,w>$边转移到$v$上，再加上原来就有的$v$的子树的，就是整棵树到$v$的贡献。

最后你再异或个$M$即可。

代码

#include <bits/stdc++.h>
using namespace std;
const int maxn=1e5+10;
int n,M;
long long f[maxn][20],ans[maxn],a[20];
struct Edge{
	int from,to,w,nxt;
}e[maxn<<1];
inline int read(){
	int x=0,fopt=1;
	char ch=getchar();
	while(!isdigit(ch)){
		if(ch=='-')fopt=-1;
		ch=getchar();
	}
	while(isdigit(ch)){
		x=(x<<3)+(x<<1)+ch-48;
		ch=getchar();
	}
	return x*fopt;
}
int head[maxn],cnt;
inline void add(int u,int v,int w){
	e[++cnt].from=u;
	e[cnt].to=v;
	e[cnt].w=w;
	e[cnt].nxt=head[u];
	head[u]=cnt;
}
void dfs1(int u,int fa){
	f[u][0]=1;
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to;
		if(v==fa)continue;
		dfs1(v,u);
		ans[u]+=ans[v];
		for(int j=0;j<=15;j++){
			int w=e[i].w;
			f[u][(j+w)%16]+=f[v][j];
			ans[u]+=f[v][j]*w;
		}
	}
}
void dfs2(int u,int fa){
	for(int i=head[u];i;i=e[i].nxt){
		int v=e[i].to,w=e[i].w;
		if(v==fa)continue;
		memset(a,0,sizeof(a));//临时先开个数组存一下，因为下面还要加siz，最好不要直接更新
		int siz=0;
		for(int j=0;j<=15;j++){
			a[(j+w)%16]+=f[u][j]-f[v][((j-w)%16+16)%16];//防止下标变负
			siz+=f[v][j];
		}
		ans[v]=ans[u]+(n-2*siz)*w;
		for(int j=0;j<=15;j++)
			f[v][j]+=a[j];
		dfs2(v,u);
	}
}
int main(){
	freopen("B.in","r",stdin);
	freopen("B.out","w",stdout);
	n=read();M=read();
	for(int i=1;i<n;i++){
		int u=read(),v=read(),w=read();
		add(u,v,w);
		add(v,u,w);
	}
	dfs1(1,0);
	dfs2(1,0);
	for(int i=1;i<=n;i++){
		f[i][0]--;//刨去到自己的路径
		for(int j=0;j<=15;j++)
			ans[i]+=((j^M)-j)*f[i][j];//加上异或后相差的值，另外还是老问题异或的优先级
		printf("%lld\n",ans[i]);
	}
	return 0;
}