LG2052 [NOI2011]道路修建

题意

在 W 星球上有 n 个国家。为了各自国家的经济发展，他们决定在各个国家 之间建设双向道路使得国家之间连通。但是每个国家的国王都很吝啬，他们只愿 意修建恰好 n – 1 条双向道路。 每条道路的修建都要付出一定的费用，这个费用等于道路长度乘以道路两端 的国家个数之差的绝对值。例如，在下图中，虚线所示道路两端分别有 2 个、4 个国家，如果该道路长度为 1，则费用为 1×|2 – 4|=2。图中圆圈里的数字表示国 家的编号。



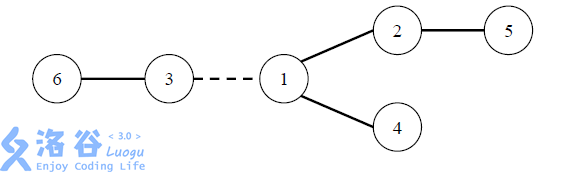
由于国家的数量十分庞大，道路的建造方案有很多种，同时每种方案的修建 费用难以用人工计算，国王们决定找人设计一个软件，对于给定的建造方案，计 算出所需要的费用。请你帮助国王们设计一个这样的软件。

\(n \leq 10^6\)

分析

照题目模拟就行了。

时间复杂度\(O(n)\)

#include<cstdlib>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<iostream>
#include<string>
#include<vector>
#include<list>
#include<deque>
#include<stack>
#include<queue>
#include<map>
#include<set>
#include<bitset>
#include<algorithm>
#include<complex>
#define rg register
#define il inline
#define co const
#pragma GCC optimize ("O0")
using namespace std;
template<class T> il T read(T&x)
{
    T data=0;
	int w=1;
    char ch=getchar();
    while(!isdigit(ch))
    {
		if(ch=='-')
			w=-1;
		ch=getchar();
	}
    while(isdigit(ch))
        data=10*data+ch-'0',ch=getchar();
    return x=data*w;
}
typedef long long ll;
const int INF=0x7fffffff;
const int MAXN=1e6+7;
int n;
struct Edge
{
	int nx,to,w;
}E[MAXN<<1];
int head[MAXN],ecnt;
void addedge(int x,int y,int w)
{
	E[++ecnt].to=y,E[ecnt].w=w;
	E[ecnt].nx=head[x],head[x]=ecnt;
}
ll ans;
int siz[MAXN];
void dfs(int x,int f)
{
	siz[x]=1;
	for(int i=head[x];i;i=E[i].nx)
	{
		int y=E[i].to,w=E[i].w;
		if(y==f)
			continue;
		dfs(y,x);
		siz[x]+=siz[y];
		ans += (ll) abs(n-2*siz[y]) * w;
	}
}
int main()
{
//  freopen(".in","r",stdin);
//  freopen(".out","w",stdout);
	read(n);
	for(int i=1;i<n;++i)
	{
		int x,y,w;
		read(x);read(y);read(w);
		addedge(x,y,w);
		addedge(y,x,w);
	}
	dfs(1,0);
	printf("%lld\n",ans);
//  fclose(stdin);
//  fclose(stdout);
    return 0;
}