【BZOJ2589】[SPOJ10707]Count on a tree II

【BZOJ2589】[SPOJ10707]Count on a tree II

题面

bzoj

题解

这题如果不强制在线就是一个很\(sb\)的莫队了，但是它强制在线啊\(qaq\)

所以我们就用到了另一个东西：树分块

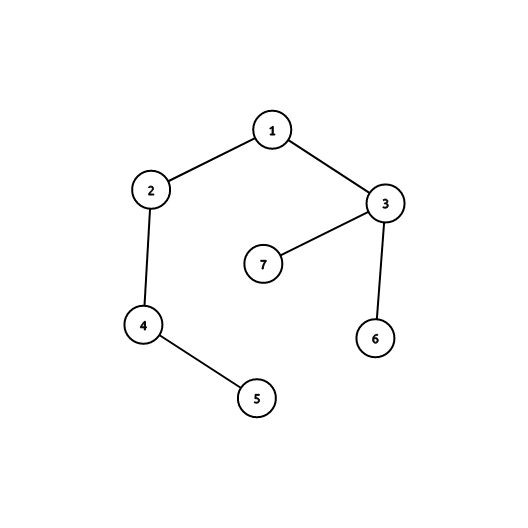
具体是怎么分块的呢：根据深度，从最深的叶子节点往上分，同一子树内的节点在一个块

比如说上面那张图，

有\(7\)个点，那么我们每隔\(2\)的深度就分一块

但是我们又要保证同一子树内的在一块，且要从最深的叶子节点一直往下

所以最后分块的结果：\((1,2)(7,6,3)(4,5)\)。

知道怎么分块了，我们在来考虑怎么做。

现在给了你两个将询问的点\(u,v(dep[u]>dep[v])\)，我们分类讨论一下现在的情况：

\((1):\)这两个点在同一个块内:

直接暴力统计即可

\((2):\)这两个点不在同一个块内：

这种情况比较复杂，记一个块的根为\(rt[i]\)，则它到另外所有点的答案我们可以很轻松地

统计出来，只需要对于每个\(rt[i]\)暴力统计一遍就可以了。

那么现在我们要考虑的只有\(u\)到它的块的根\(x\)路径上是否会对答案产生贡献：

对于这个，我们可以将这个分块可持久化，维护这个点的颜色在它的祖先中出现最深的位置

的深度，那么一个块只需继承上面的块，并将在这个块中颜色的答案更新，因为那个颜色如

果出现在这个位置，那么答案肯定更优。

有了上面的铺垫，那我们只需对\(u\rightarrow x\)上的点暴力算它的深度是否超过\(lca_{u,v}\)即可

代码

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <algorithm>
using namespace std;
inline int gi() {
    register int data = 0, w = 1;
    register char ch = 0;
    while (!isdigit(ch) && ch != '-') ch = getchar();
    if (ch == '-') w = -1, ch = getchar();
    while (isdigit(ch)) data = 10 * data + ch - '0', ch = getchar();
    return w * data;
}
const int MAX_N = 4e4 + 5;
struct Graph { int to, next; } e[MAX_N << 1]; int fir[MAX_N], e_cnt;
void clearGraph() { memset(fir, -1, sizeof(fir)); e_cnt = 0; }
void Add_Edge(int u, int v) { e[e_cnt] = (Graph){v, fir[u]}; fir[u] = e_cnt++; }
int N, M, LEN;
int X[MAX_N], a[MAX_N], b[MAX_N], r[MAX_N];
int P[MAX_N][205], A[205][MAX_N];
int fa[MAX_N], dep[MAX_N], q[MAX_N], belong[MAX_N], cur, sz;
int rt[205], tot;
int c[MAX_N], Res;
struct Block {
    int a[205];
    int &operator [] (int x) { return P[a[b[x]]][r[x]]; }
    void insert(Block rhs, int x, int d) {
        int blk = b[x], t = r[x];
        memcpy(a, rhs.a, sizeof(a));
        memcpy(P[++sz], P[a[blk]], sizeof(P[0]));
        P[sz][t] = d, a[blk] = sz;
    }
} s[MAX_N]; 
namespace Tree {
    int top[MAX_N], son[MAX_N], size[MAX_N];
    void dfs(int x, int tp) {
        top[x] = tp;
        if (son[x]) dfs(son[x], tp);
        for (int i = fir[x]; ~i; i = e[i].next) {
            int v = e[i].to; if (v == fa[x] || v == son[x]) continue;
            dfs(v, v);
        }
    }
    int LCA(int x, int y) {
        while (top[x] != top[y]) {
            if (dep[top[x]] < dep[top[y]]) swap(x, y);
            x = fa[top[x]];
        }
        return dep[x] < dep[y] ? x : y;
    }
}
int dfs(int x, int f) {
    fa[x] = f;
    s[x].insert(s[f], a[x], dep[x] = dep[f] + 1);
    Tree::size[x] = 1;
    q[++cur] = x; int md = dep[x], p = cur;
    for (int i = fir[x]; ~i; i = e[i].next) {
        int v = e[i].to; if (v == f) continue;
        md = max(md, dfs(v, x)); Tree::size[x] += Tree::size[v];
        if (Tree::size[Tree::son[x]] < Tree::size[v]) Tree::son[x] = v;
    }
    if (md - dep[x] >= LEN || p == 1) {
        rt[++tot] = x;
        for (int i = p; i <= cur; i++) belong[q[i]] = tot;
        cur = p - 1;
        return dep[x] - 1;
    }
    return md;
}
void Prepare(int x, int f, int *s) {
    if (!c[a[x]]++) ++Res; s[x] = Res;
    for (int i = fir[x]; ~i; i = e[i].next) if (e[i].to != f) Prepare(e[i].to, x, s);
    if (!--c[a[x]]) --Res;
}
int Solve1(int u, int v) {
    for (cur = Res = 0; u != v; u = fa[u]) {
        if (dep[u] < dep[v]) swap(u, v);
        if (!c[q[++cur] = a[u]]) c[a[u]] = 1, ++Res;
    }
    for (Res += !c[a[u]]; cur; ) c[q[cur--]] = 0;
    return Res;
}
int Solve2(int u, int v) {
    if (dep[rt[belong[u]]] < dep[rt[belong[v]]]) swap(u, v);
    int x = rt[belong[u]], d = dep[Tree::LCA(u, v)]; Res = A[belong[u]][v];
    for (cur = 0; u != x; u = fa[u]) {
        if (!c[a[u]] && s[x][a[u]] < d && s[v][a[u]] < d)
            c[q[++cur] = a[u]] = 1, ++Res;
    }
    for (; cur; ) c[q[cur--]] = 0;
    return Res;
}
int main () {
    clearGraph();
    N = gi(), M = gi(); LEN = sqrt(N) - 1;
    for (int i = 1; i <= N; i++) b[i] = (i - 1) / LEN + 1, r[i] = i % LEN;
    for (int i = 1; i <= N; i++) a[i] = X[i] = gi();
    sort(&X[1], &X[N + 1]); int cnt = unique(&X[1], &X[N + 1]) - X - 1;
    for (int i = 1; i <= N; i++) a[i] = lower_bound(&X[1], &X[cnt + 1], a[i]) - X;
    for (int i = 1; i < N; i++) {
        int u = gi(), v = gi();
        Add_Edge(u, v);
        Add_Edge(v, u);
    }
    cur = 0;
    dfs(1, 0); Tree::dfs(1, 1);
    for (int i = 1; i <= tot; i++) Prepare(rt[i], 0, A[i]); 
    for (int ans = 0; M--; ) {
        int u = ans ^ gi(), v = gi();
        printf("%d\n", ans = belong[u] == belong[v] ? Solve1(u, v) : Solve2(u, v));
    }
    return 0;
}