第十五章——自编码器（Autoencoders）

自编码器是一种能够通过无监督学习，学到输入数据高效表示的人工神经网络。输入数据的这一高效表示称为编码（codings），其维度一般远小于输入数据，使得自编码器可用于降维（查看第八章）。更重要的是，自编码器可作为强大的特征检测器（feature detectors），应用于深度神经网络的预训练（查看第十一章）。此外，自编码器还可以随机生成与训练数据类似的数据，这被称作生成模型（generative model）。比如，可以用人脸图片训练一个自编码器，它可以生成新的图片。

自编码器通过简单地学习将输入复制到输出来工作。这一任务（就是输入训练数据，再输出训练数据的任务）听起来似乎微不足道，但通过不同方式对神经网络增加约束，可以使这一任务变得极其困难。比如，可以限制内部表示的尺寸（这就实现降维了），或者对训练数据增加噪声并训练自编码器使其能恢复原有。这些限制条件防止自编码器机械地将输入复制到输出，并强制它学习数据的高效表示。简而言之，编码（就是输入数据的高效表示）是自编码器在一些限制条件下学习恒等函数（identity function）的副产品。（这句话有点抽象，不过看完15.1就明白了）

15.1 高效的数据表示

下面有两组数字，哪组更容易记忆呢？

40, 27, 25, 36, 81, 57, 10, 73, 19, 68
50, 25, 76, 38, 19, 58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20

乍一看可能觉得第一行数字更容易记忆，毕竟更短。但仔细观察就会发现，第二组数字是有规律的：偶数后面是其二分之一，奇数后面是其三倍加一（这就是著名的hailstone sequence）。如果识别出了这一模式，第二组数据只需要记住这两个规则、第一个数字、以及序列长度。如果你的记忆能力超强，可以记住很长的随机数字序列，那你可能就不会去关心一组数字是否存在规律了。所以我们要对自编码器增加约束来强制它去探索数据中的模式。

记忆（memory）、感知（perception）、和模式匹配（pattern matching）的关系在1970s早期就被William Chase和Herbert Simon研究过。他们发现国际象棋大师观察棋盘5秒，就能记住所有棋子的位置，而常人是无法办到的。但棋子的摆放必须是实战中的棋局（也就是棋子存在规则，就像第二组数字），棋子随机摆放可不行（就像第一组数字）。象棋大师并不是记忆力优于我们，而是经验丰富，很擅于识别象棋模式，从而高效地记忆棋局。

和棋手的记忆模式类似，一个自编码器接收输入，将其转换成高效的内部表示，然后再输出输入数据的类似物。自编码器通常包括两部分：encoder（也称为识别网络）将输入转换成内部表示，decoder（也称为生成网络）将内部表示转换成输出。（如图15-1）

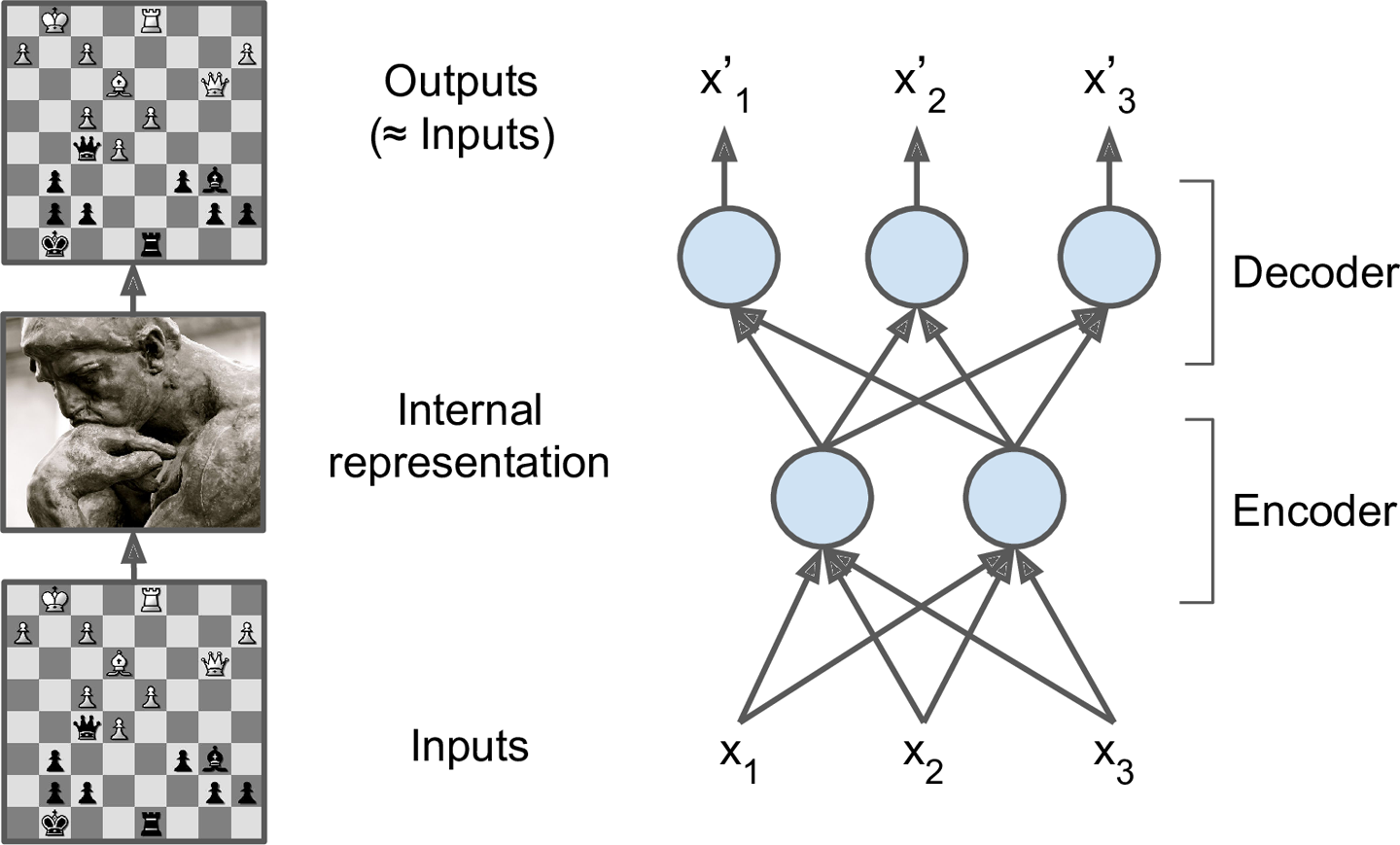
图15-1 象棋大师的记忆模式（左）和一个简单的自编码器

正如上图所示，自编码器的结构和多层感知机（查看第十章）类似，除了输入神经元和输出神经元的个数相等。在上图的例子中，自编码器只有一个包含两个神经元的隐层（encoder），以及包含3个神经元的输出层（decoder）。输出是在设法重建输入，损失函数是重建损失（reconstruction loss）。

由于内部表示（也就是隐层的输出）的维度小于输入数据（用2D取代了原来的3D），这称为不完备自编码器（undercomplete autoencoder）。

undercomplete应该是个数学概率，不用深究了，毕竟在Wikipedia上面的解释只有一句话：Describing a frame (in linear algebra) having a set of functions less than a basis。

15.2 不完备线性自编码器实现PCA（Performing PCA with an Undercomplete Linear Autoencoder）

如果自编码器使用线性激活函数并且损失函数是均方差（Mean Squared Error，MSE），那它就可以用来实现主成分分析（查看第八章）。

下面的代码实现了一个简单的线性自编码器，将3D数据投影为2D：

import tensorflow as tf

from tensorflow.contrib.layers import fully_connected

n_inputs = 3 # 3D inputs

n_hidden = 2 # 2D codings

n_outputs = n_inputs

learning_rate = 0.01

X = tf.placeholder(tf.float32, shape=[None, n_inputs])

hidden = fully_connected(X, n_hidden, activation_fn=None)

outputs = fully_connected(hidden, n_outputs, activation_fn=None)

reconstruction_loss = tf.reduce_mean(tf.square(outputs - X)) # MSE

optimizer = tf.train.AdamOptimizer(learning_rate)

training_op = optimizer.minimize(reconstruction_loss)

init = tf.global_variables_initializer()

然后载入数据集，在训练集上训练模型，并对测试集进行编码（也就是投影为2D）：

X_train, X_test = [...] # load the dataset

n_iterations = 1000

codings = hidden # the output of the hidden layer provides the codings

with tf.Session() as sess:

    init.run()

    for iteration in range(n_iterations):

        training_op.run(feed_dict={X: X_train}) # no labels (unsupervised)

    codings_val = codings.eval(feed_dict={X: X_test})

15.3 栈式自编码器（Stacked Autoencoders）

和其他的神经网络一样，自编码器可以有多个隐层，这被称作栈式自编码器（或者深度自编码器）。增加隐层可以学到更复杂的编码，但千万不能使自编码器过于强大。想象一下，一个encoder过于强大，它仅仅是学习将输入映射为任意数（然后decoder学习其逆映射）。很明显这一自编码器可以很好的重建数据，但它并没有在这一过程中学到有用的数据表示。（而且也不能推广到新的实例）

栈式自编码器的架构一般是关于中间隐层对称的，如图15-3所示。

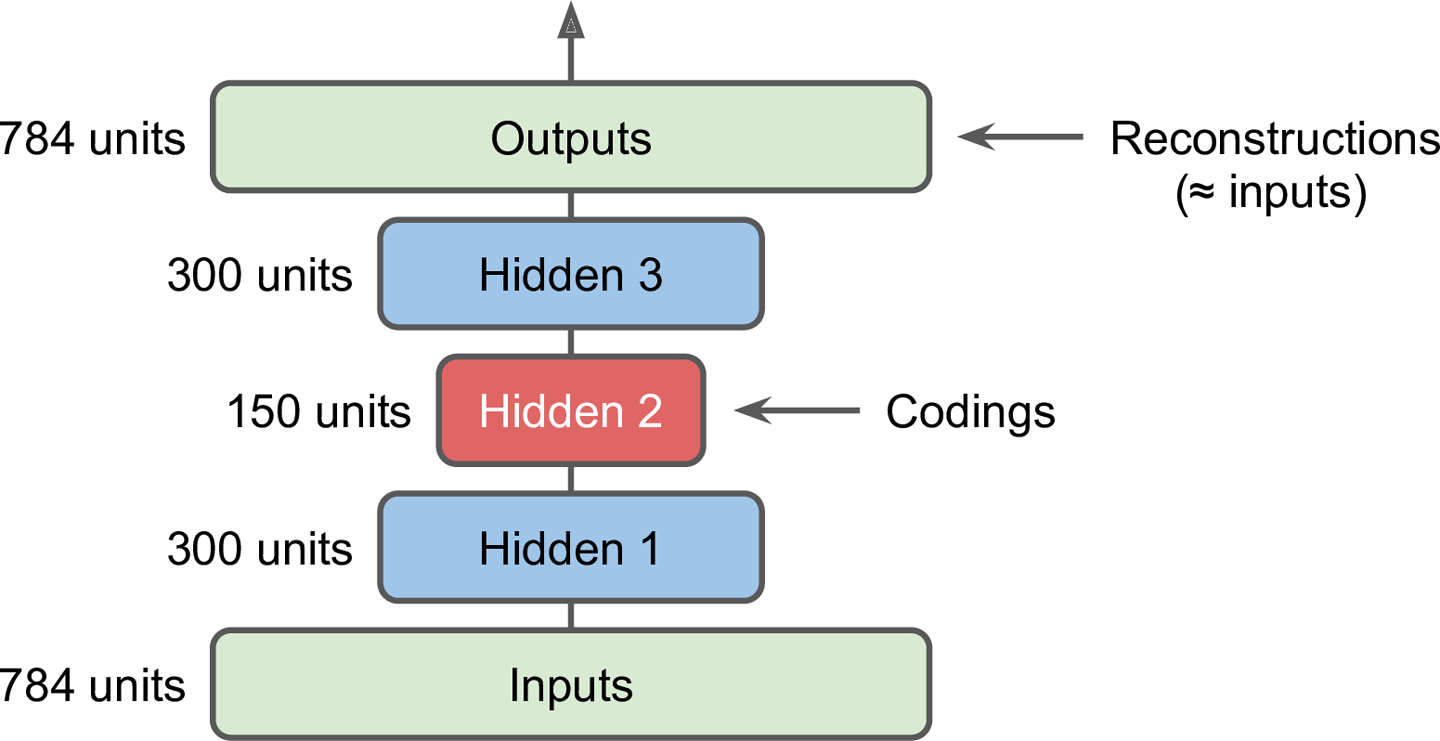
图15-3 栈式自编码器

15.3.1 TensorFlow 实现

参考：本书代码

15.3.2 捆绑权重

如果一个自编码器的层次是严格轴对称的（如图15-3），一个常用的技术是将decoder层的权重捆绑到encoder层。这使得模型参数减半，加快了训练速度并降低了过拟合风险。具体的，假设自编码器一共有$N$层（不算输入层），$W_L$表示第$L$层的权重（例如，第一层是第一个隐层，第$\frac{2}{N}$层是编码层，第$N$层是输出层），那么decoder层的权重可以表示为$W_{N-L+1} = W_L^T \ , L = 1,2,\cdots ,\frac{N}{2}$。

不过偏置项不会捆绑。

15.3.3 一次训练一个自编码器

与之前训练整个栈式自编码器不同，可以训练多个浅层的自编码器，然后再将它们合并为一体，这样要快得多。如图15-4

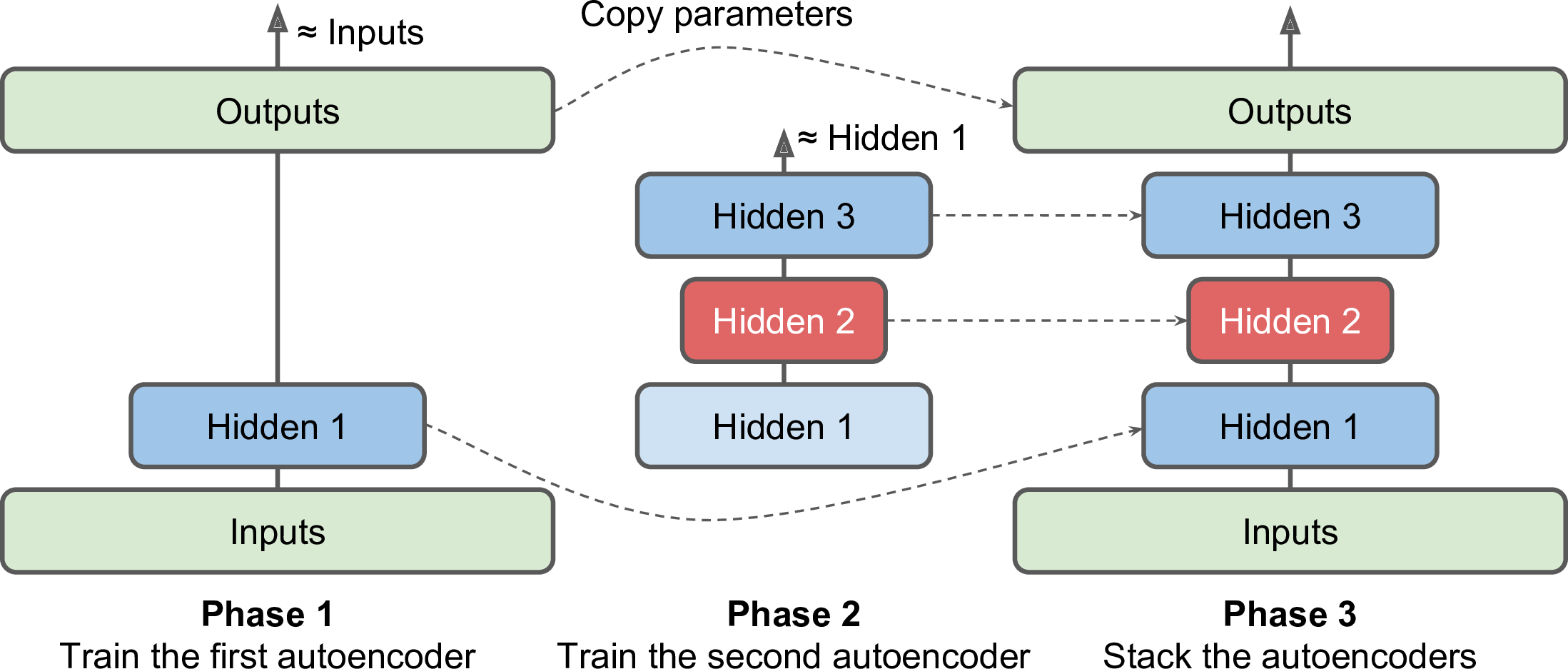
图15-4 一次训练一个浅层自编码器

首先，第一个自编码器学习去重建输入。然后，第二个自编码器学习去重建第一个自编码器隐层的输出。最后，这两个自编码器被整合到一起，如图15-4。可以使用这种方式，创建一个很深的栈式自编码器。

另一个实现方法首先创建一个包含完整栈式编码器的图，然后再每一个训练时期增加额外的操作，如图15-5：

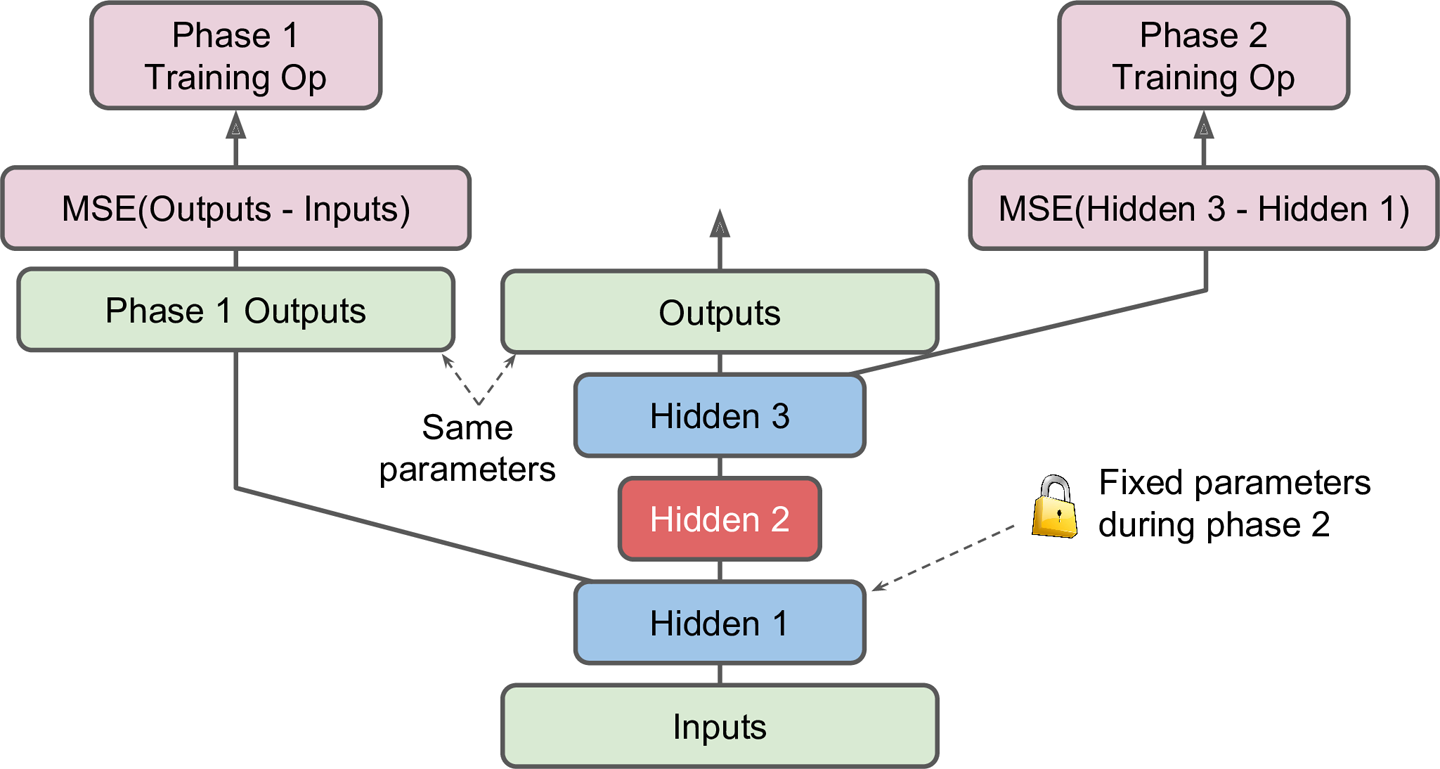
图15-5

其中，

中间的一列是完整的栈式编码器，这部分在训练完成之后可以使用。
左侧一列是最先需要训练的，它跳过第二和第三个隐层，直接创建一个输出层。这个输出层与栈式自编码器的输出层共享同样的权重和偏置。
随后是右侧一列的训练。它使得第三个隐层的输出与第一个隐层的输出尽可能的接近。

15.4 使用栈式自编码器进行无监督预训练

正如第十一章所讨论的，如果我们要处理一个复杂的有监督学习问题又没有足够的标注数据，一个解决方案是找到一个解决类似任务的训练好的模型，复用低层。类似的，如果有一个很大的数据集但绝大部分是未标注数据，可以使用所有的数据先训练一个栈式自编码器，然后复用低层来完成真正的任务。如图15-8所示：

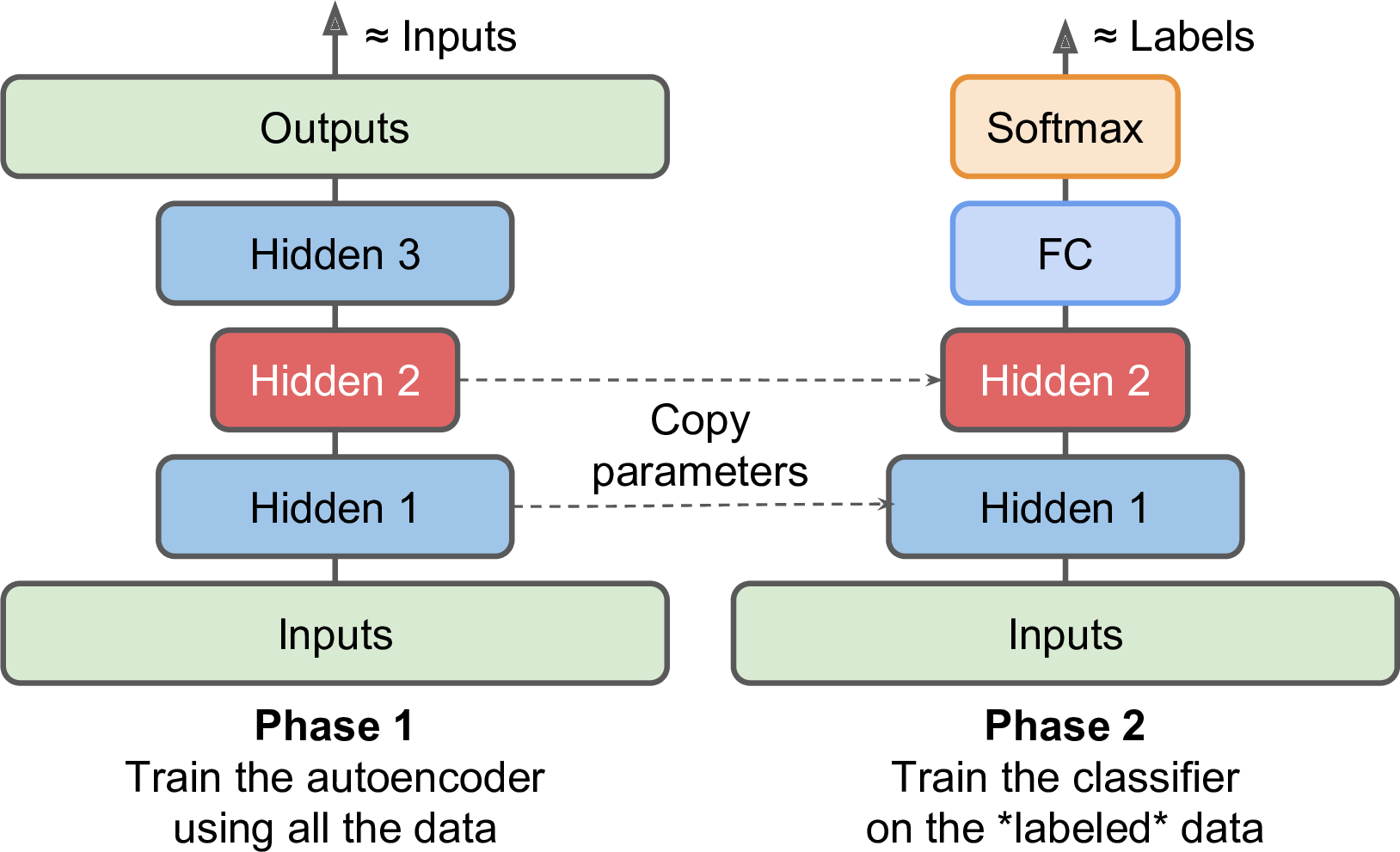
图15-8 使用自编码器进行无监督预训练

15.5 去噪自编码器

另一种强制自编码器学习有用特征的方式是最输入增加噪声，通过训练之后得到无噪声的输出。这防止了自编码器简单的将输入复制到输出，从而提取出数据中有用的模式。如图15-9左侧所示。

使用自编码器去燥的思想在1980s提出（比如，在1987年Yann LeCun的硕士论文中有所提及）。在一篇2008年的论文中，Pascal Vincent等人表明自编码器可用于特征提取。在一篇2010年的论文中，Vincent等人提出栈式去燥自编码器（stacked denoising autoencoders）。

噪声可以是添加到输入的纯高斯噪声，也可以是随机丢弃输入层的某个特征，类似于dropout。如图15-9右侧所示。

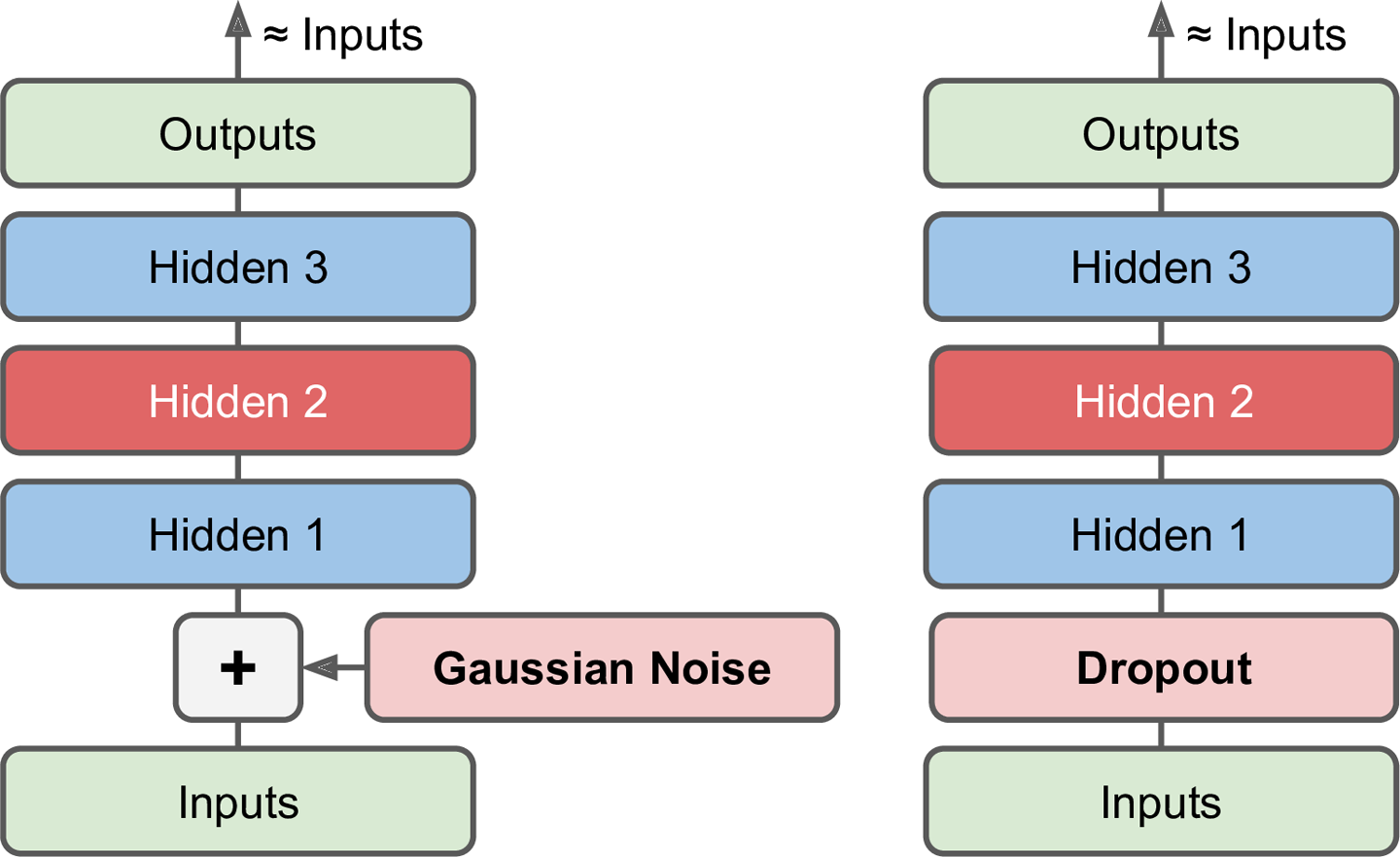
图15-9 图中自编码器，通过高斯噪声（左）或者Dropout（右）