CH Round #55 - Streaming #6 (NOIP模拟赛day2)解题报告

T1九九归一

描述

萌蛋在练习模n意义下的乘法时发现，总有一些数，在自乘若干次以后，会变成1。例如n=7，那么5×5 mod 7=4,4×5 mod 7=6,6×5 mod 7=2,2×5 mod 7=3,3×5 mod 7=1。如果继续乘下去，就会陷入循环当中。
萌蛋还发现，这个循环的长度经常会是φ(n)，即小于n且与n互质的正整数的个数。例如，φ(7)=6，而上述循环的长度也是6，因为5,4,6,2,3,1共有6个数。
再如n=6，那么5×5 mod 6=1。这个循环的长度很短，只有2，而恰好φ(6)=2。
然而，对于某些情况，虽然循环的长度可以是φ(n)，但存在比φ(n)更小的长度：例如n=7，而2×2 mod 7=4,4×2 mod 7=1，循环的长度只有3。当然，6也可以是一个循环的长度。
假设已知了n，我们称数a神奇的，当且仅当关于数a的循环长度可以是φ(n)，而且不存在比φ(n)更小长度的循环。例如对于n=7，5是神奇的，而2不是神奇的。
现在给出n和q次询问，每次询问给出a，问a是否是神奇的。

输入格式

第一行两个整数n q。n≤10,000,000,q≤100,000,0≤a<n。
第二行有q个整数，每个表示一个a。

输出格式

输出q个字符，1表示这个数是神奇的，0表示这个数不是神奇的。

样例输入

7 3
5 2 0

样例输出

100
首先我们用O(sqrt(n))的时间求出fai(n)，然后对于每一个数a，进行一次快速幂算出afai(n)Mod n是否为1，不为1则直接输出0即可。
题目中已经告知循环的长度必定为fai(n)的因数，那么我们事先用sqrt(n)的时间求出fai(n)的所有因数，那么一个数的因数是log(n)级别的，于是对于每一个因数进行快速幂判断是否神奇，总复杂度loglogn

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <cstdlib>
 #include <cmath>
 #include <algorithm>
 #include <queue>
 #include <stack>
 #include <map>
 #include <set>
 #include <list>
 #include <vector>
 #include <ctime>
 #include <iterator>
 #include <functional>
 #define pritnf printf
 #define scafn scanf
 #define For(i,j,k) for(int i=(j);i<=(k);(i)++)
 using namespace std;
 typedef long long LL;
 typedef unsigned int Uint;
 const int INF=0x7ffffff;
 //==============struct declaration==============
 
 //==============var declaration=================
 LL bound;
 vector <LL> fact;
 int siz;
 //==============function declaration============
 int fai(LL x);
 int gcd(LL a,LL b){return a%b==?b:gcd(b,a%b);}
 bool loop(LL x,LL Mod);
 void divide(LL x);
 LL quickpow(int x,int Exp,LL Mod);
 //==============main code=======================
 int main()
 {
   LL Mod,q;
   scanf("%lld%lld",&Mod,&q);
   bound=fai(Mod);divide(bound);
   while (q--){
     LL query;
     scanf("%lld",&query);
     if (gcd(query,Mod)!=)//可以证明如果不互质是不可能循环的
                                      //此处用quickpow亦可，时间复杂度均为log(n)
       putchar('');
     else if (loop(query,Mod))
       putchar('');
     else
       putchar('');
   }
   return ;
 }
 //================fuction code====================
 int fai(LL x)//欧拉函数
 {
    LL res=x;
    LL m=sqrt(x+0.5);
    for(LL i=;i<=m;i++){
      if (x%i==){
        res=res/i*(i-);
        while (x%i==)
          x/=i;
      }
    }
    if (x!=)
      res=res/x*(x-);
    return res;
 }
 bool loop(LL x,LL Mod)//判断是否神奇
 {
   for(int i=;i<=siz;i++)
     if (quickpow(x,fact[i],Mod)==)
       return false;
   return true;
 }
 void divide(LL x)//分解因数
 {
   int m=sqrt(x+0.5);
   For(i,,m)
     if (x%i==){
       fact.push_back(i);
       fact.push_back(x/i);
     }
   sort(fact.begin(),fact.end());
   siz=fact.size()-;
 }
 LL quickpow(int x,int Exp,LL Mod)//快速幂
 {
   if (Exp==)
     return ;
   if (Exp==)
     return x;
   LL t=quickpow(x,Exp/,Mod);
   t=(t*t)%Mod;
   if (Exp&)
     t=(t*x)%Mod;
   return t;
 }

T1代码

T2 LCA的统计

描述

萌蛋有一棵n个节点的有根树，其根节点为1。除此之外，节点i的父节点为p_i。每个点上都有一个权值，节点i的权值是w_i。
萌蛋知道你一定知道什么叫做祖先（从根到某个点的路径上的每个点都是这个点的祖先，包括它本身），也一定知道什么叫做最近公共祖先（两个点的最近公共祖先是某个点，这个点同时是两个点的祖先，且离根最远）。
现在给出这棵树，你需要求出：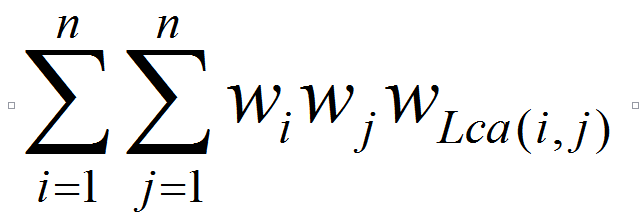

其中LCA(i,j)表示点i与点j的最近公共祖先。
由于答案可能很大，你只需要输出它对1,000,000,007取模的结果。

输入格式

第一行为两个整数n w_1。1≤n≤100,000,0≤w_i≤1,000,000,000,1≤p_i<i
第二行到第n行，第i行有两个整数p_i  w_i。

输出格式

输出只有一行，为一个整数，表示所求答案对1,000,000,007取模的结果。

样例输入

2 2
1 1

样例输出

17

怎么说呢。这道题我其实考试的时候想了很久，没有想到什么好的算法，我的算法是O(n*deg²)其中deg表示这个树的度。那么针对这个复杂度应该是很容易TLE的。但是由于题目数据淼，还是AC了。

然后我发现标程也是用的这个办法。。。虽然不严谨，但是还是给出思路（记S_i为以i为祖先点的所有点的W和（包括i节点本身））

对于每一个节点k，统计以它为LCA的节点，分为三部分：

一、i=j=k  ans+=w_k*w_k*w_k

二、i=k,j是i的孩子  ans+=2*(w_k*w_k*(S_k-W_k))

应该没有问题吧由于i,j可以互换，所以*2

三、i,j分别位于k的两个不同的子树中

我们先来看只有两个子节点的情况（圈圈内数字是节点编号）

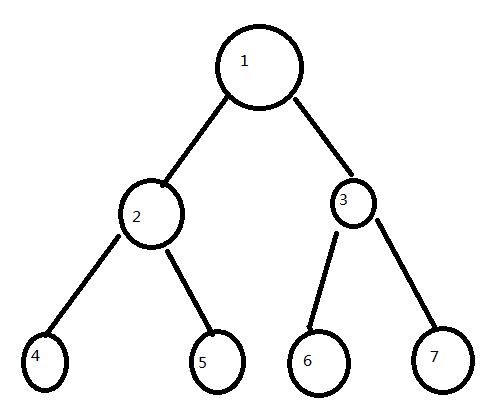
对于1号节点进行统计i,j分别在左右子树的情况

w1*w2w3  w1*w2w6 w1*w2w7

w1*w4w3  w1*w4w6 w1*w4w7

w1*w5w3  w1*w5w7 w1*w5w7

以上加起来就是：

w1*(w2+w4+w5)(w3+w6+w7)=w1*S₂*S₃

最后*2，因为i,j可以调换

三叉、四叉直到n叉数都可以对每两个子树进行分别统计。

然后。。做完了吧。。记得对1,000,000,007取模就行

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <cstdlib>
 #include <cmath>
 #include <algorithm>
 #include <queue>
 #include <stack>
 #include <map>
 #include <set>
 #include <list>
 #include <vector>
 #include <ctime>
 #include <iterator>
 #include <functional>
 #define pritnf printf
 #define scafn scanf
 #define For(i,j,k) for(int i=(j);i<=(k);(i)++)
 using namespace std;
 typedef long long LL;
 typedef unsigned int Uint;
 const int INF=0x7ffffff;
 //==============struct declaration==============
 
 //==============var declaration=================
 const int MAXN=;
 const int MOD=;
 vector <int> Edge[MAXN];
 LL w[MAXN],S[MAXN],res=;
 int n;
 //==============function declaration============
 void Count(int x);//计算以x为LCA的答案
 //==============main code=======================
 int main()
 {
   scanf("%d%lld",&n,&w[]);
   For(i,,n){
     int pa;
     scanf("%d%lld",&pa,&w[i]);
     Edge[pa].push_back(i);
   }
   Count();
   printf("%lld\n",res%MOD);
   return ;
 }
 //================fuction code====================
 void Count(int x)
 {
   res=(res+(((w[x]*w[x])%MOD)*w[x])%MOD)%MOD;//情况1
   S[x]=w[x];
   int siz=Edge[x].size()-;
   For(i,,siz){
     Count(Edge[x][i]);//对子节点递归处理
     res=(res+((w[x]*w[x])%MOD*(S[Edge[x][i]]*)%MOD)%MOD)%MOD;//情况2
     S[x]=(S[x]+S[Edge[x][i]])%MOD;//累加S值
   }
   For(i,,siz)
     For(j,i+,siz)
       res=(res+((((w[x]*S[Edge[x][i]])%MOD*S[Edge[x][j]])%MOD)*)%MOD)%MOD;//情况3
   return;
 }

T2代码

T3 四驱兄弟

描述

如果你和萌蛋一样，也看过《四驱兄弟》，你或许会记得，有一局比赛十分特别，只按照5个人中的第4名计算成绩。
现在我们将问题扩展一下：一共有n个队员，只按照其中的第k名计算成绩。而赛车的规则也有所不同：一共有m个赛车，每个赛车装配着2个GP晶片的终端，且第i个赛车预期到达终点的时间为a_i。（注：不同赛车上的终端可以对应着相同的GP晶片，但不会2个都相同；任何赛车上的2个终端对应的GP晶片都是不同的）
比赛开始时，n个队员依次选择自己的赛车。对于每个队员，他可以选择开启GP晶片功能或不开启。如果开启，那么2个终端对应的GP晶片就会建立连接，且这个赛车的比赛用时就是预期时间a_i；如果不开启，那么GP晶片不会建立连接，但是这个赛车的比赛用时将会非常长（可以认为是无穷）。甚至，他可以放弃比赛，这样他不会占用任何赛车，但是当然比赛用时也会被认为是无穷。
任何时候，一旦存在若干个（至少3个）晶片A,B,C,…,X满足：A与B建立了连接，B与C建立了连接，……，X与A建立了连接（即形成了循环连接的情况），那么处理系统就会崩溃。这是非常可怕的，我们宁可让比赛用时变为无穷也不能让系统崩溃。
现在给出队员和赛车的信息，请输出最优情况下的成绩（即第k小的比赛时间的最小值）。为了增大难度，k并不是给出的，而是你需要对于1≤k≤n的所有的k输出答案。

输入格式

第一行为两个整数n m。
接下来m行，每行描述了一个赛车，格式为空格隔开的一个整数和两个字符串，分别是a_i和它的两个终端对应的GP晶片名。

输出格式

n行，每行一个整数，第i行表示i=k时的答案。特别地，如果答案是无穷，输出INF。

样例输入

3 3
95 GP_1 GP_2
100 GP_1 gp@3
100 gp@3 GP_2

样例输出

95
100
INF

数据范围与约定

对于20%的数据，n,m≤3，GP晶片名称的长度均为1。
对于40%的数据，n,m≤6，GP晶片名称的长度均为1。
对于60%的数据，n,m≤1,000，GP晶片的长度不会超过3。
对于100%的数据，0<n,m≤100,000，0<a_i≤1,000,000,000，GP晶片的名称只包含大小写字母、数字、“@” 、“_”共64种字符且长度不会超过5且非空。

样例解释

以下是一种最优方案（方案可能不唯一）：
首先，3人各自选择了1辆赛车。（都没有放弃参赛）
如果k=1，那么让赛车1开启GP晶片，其余不开启，此时3个赛车的比赛时间分别为95，INF，INF，第1名的成绩是95。
如果k=2，那么让赛车2和3开启GP晶片，而赛车1不开启，此时3个赛车的比赛时间分别为100，100，INF，第2名的成绩是100。
如果k=3，那么由于3辆赛车不可能都开启GP晶片（因为假设都开启，那么3个GP晶片会出现循环连接的情况，这是不允许的），所以总有赛车没有开启GP晶片，那么第3名的成绩一定是INF。

iostream害人啊！！本来可以AK的就是因为cin超时了。。。最后一题只有80分。我还写了ios::sync_with_stdio(false)都超时。。等等测试一下不开有多少分。

很简单的一个模型。将一辆赛车看成一条边，连接两个不同的芯片，边长为速度，那么这一题就改成了选n条边，使得图中不出现环，且对于k∈[1,n]来说，第k大的边最小。

那么。。最小生成树。。

证明自行搜索克鲁斯卡尔算法的证明，基本类似。

 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <cstdlib>
 #include <cmath>
 #include <algorithm>
 #include <queue>
 #include <stack>
 #include <map>
 #include <set>
 #include <list>
 #include <vector>
 #include <ctime>
 #include <iterator>
 #include <functional>
 #define pritnf printf
 #define scafn scanf
 #define For(i,j,k) for(int i=(j);i<=(k);(i)++)
 using namespace std;
 typedef long long LL;
 typedef unsigned int Uint;
 const int INF=0x7ffffff;
 //==============struct declaration==============
 struct adj{
   int s,e,len;
   bool operator <(const adj &rhs)const {
     return len<rhs.len;
   }
 };
 //==============var declaration=================
 map <string,int> id;
 const int MAXN=;
 adj Edge[MAXN];
 int n,m,tot=;
 int root[MAXN*];
 //==============function declaration============
 int findr(int x){return root[x]==x?x:root[x]=findr(root[x]);}
 //==============main code=======================
 int main()
 {
   id.clear();
   scanf("%d%d",&n,&m);
   For(i,,m){
     char str1[],str2[];
     string str;
     scanf("%d%s%s",&Edge[i].len,str1,str2);
     str=string(str1);
     if (id[str]==)
       id[str]=++tot;
     Edge[i].s=id[str];
     str=string(str2);
     if (id[str]==)
       id[str]=++tot;
     Edge[i].e=id[str];
   }
   sort(Edge+,Edge++m);
   For(i,,tot)
     root[i]=i;
   for(int i=;i<=m&&n>;i++){
     adj &e=Edge[i];
     if (findr(e.s)!=findr(e.e)){
       printf("%d\n",e.len);
       n--;
       root[findr(e.s)]=findr(e.e);
     }
   }
   while (n--)
     printf("INF\n");
   return ;
 }
 //================fuction code====================

T3代码

比赛网址：http://ch.ezoj.tk/contest/CH%20Round%20%2355%20-%20Streaming%20%236%20(NOIP%E6%A8%A1%E6%8B%9F%E8%B5%9Bday2)