Codeforces Round #329 (Div. 2) D. Happy Tree Party LCA/树链剖分

D. Happy Tree Party

 

 

Bogdan has a birthday today and mom gave him a tree consisting of n vertecies. For every edge of the tree i, some number xi was written on it. In case you forget, a tree is a connected non-directed graph without cycles. After the present was granted, m guests consecutively come to Bogdan's party. When the i-th guest comes, he performs exactly one of the two possible operations:

1. Chooses some number yi, and two vertecies ai and bi. After that, he moves along the edges of the tree from vertex ai to vertex biusing the shortest path (of course, such a path is unique in the tree). Every time he moves along some edge j, he replaces his current number yi by 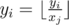, that is, by the result of integer division yi div xj.
2. Chooses some edge pi and replaces the value written in it xpi by some positive integer ci < xpi.

As Bogdan cares about his guests, he decided to ease the process. Write a program that performs all the operations requested by guests and outputs the resulting value yi for each i of the first type.

Input

 

The first line of the input contains integers, n and m (2 ≤ n ≤ 200 000, 1 ≤ m ≤ 200 000) — the number of vertecies in the tree granted to Bogdan by his mom and the number of guests that came to the party respectively.

Next n - 1 lines contain the description of the edges. The i-th of these lines contains three integers ui, vi and xi (1 ≤ ui, vi ≤ n, ui ≠ vi,1 ≤ xi ≤ 1018), denoting an edge that connects vertecies ui and vi, with the number xi initially written on it.

The following m lines describe operations, requested by Bogdan's guests. Each description contains three or four integers and has one of the two possible forms:

• 1 ai bi yi corresponds to a guest, who chooses the operation of the first type.
• 2 pi ci corresponds to a guests, who chooses the operation of the second type.

It is guaranteed that all the queries are correct, namely 1 ≤ ai, bi ≤ n, 1 ≤ pi ≤ n - 1, 1 ≤ yi ≤ 1018 and 1 ≤ ci < xpi, where xpirepresents a number written on edge pi at this particular moment of time that is not necessarily equal to the initial value xpi, as some decreases may have already been applied to it. The edges are numbered from 1 to n - 1 in the order they appear in the input.

 

Output

 

For each guest who chooses the operation of the first type, print the result of processing the value yi through the path from ai to bi.

Examples

input

 

6 6
1 2 1
1 3 7
1 4 4
2 5 5
2 6 2
1 4 6 17
2 3 2
1 4 6 17
1 5 5 20
2 4 1
1 5 1 3

output

 

2
4
20
3

题意 ：

　　给你 一棵树

　　m次询问

　　每次询问有两种 1：a,b,z

　　在a到b这条路径是上 求出 所有边权为x1,x2,x3...... 那么求出 [[[z/x1]/x2]/x3]

　　2 x y，把第x条边的边权改为y

题解：

　　我们把边权为1的 边 全部缩掉

　　那么 z最多 除 60几次 

　　用并查集就可以缩了，两个点靠近的时候 和LCA向上走 姿势差不多

 

　　或者树链剖分 对于一条链的边权修改 及 乘积我们用线段树维护也是比较裸

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

#pragma comment(linker, "/STACK:102400000,102400000")
#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define pii pair<int,int>
#define MP make_pair

typedef long long LL;
const long long INF = 1e18;
const double Pi = acos(-1.0);
const int N = 2e5+, M = 5e5+, inf = 2e9, mod = ;

LL c[N];
int head[N],t = , fv[N], f[N], deep[N], n, m, pa[N];
struct edge{int to,next,id;}e[N * ];
struct Line {
    int x,y;
    LL z;
    Line(int x = , int y = , int z = ) : x (x), y (y), z (z) {}
}L[N];
void add(int u,int v,int id) {e[t].next = head[u];e[t].to = v;e[t].id = id; head[u] = t++; }

int finds(int x) {return x == pa[x]? pa[x]:pa[x] = finds(pa[x]);}

void update(int u,int to) {
    fv[to] = fv[u];
    f[to] = f[u];
}
void dfs(int u,int fa) {
        deep[u] = deep[fa] + ;
        for(int i = head[u]; i; i = e[i].next) {
                int to = e[i].to;
                if(to == fa) continue;
                fv[to] = e[i].id;
                f[to] = u;
                if(c[e[i].id] == ) {
                    pa[to] = finds(u);
                    update(u,to);
                }
                dfs(to,u);
        }
}

LL Lca(int u,int v,LL res) {
         u = finds(u);
         v = finds(v);
        while(u != v) {
            if(deep[u] < deep[v]) swap(u,v);
           // cout<<deep[u]<<" "<<deep[v]<<" "<<fv[u]<<" "<<c[fv[u]]<<endl;
            res /= c[fv[u]];
            if(res == ) return res;
            u = finds(f[u]);
        }
        return res;
}
int main() {
        scanf("%d%d",&n,&m);
        for(int i = ; i <= n; ++i) pa[i] = i;
        for(int i = ; i < n; ++i) {
            int a,b;
            scanf("%d%d%I64d",&a,&b,&c[i]);
            add(a,b,i);add(b,a,i);
            L[i] = Line(a,b,c[i]);
        }

        c[] = ;
        fv[] = ;
        f[] = ;

        dfs(,);
        while(m --) {
            int op, x;
            LL z,y;
            scanf("%d%d%I64d",&op,&x,&y);
            if(op == ) {
                scanf("%I64d",&z);
                LL res = Lca(x,y,z);
                printf("%I64d\n",res);
            }
            else {
                c[x] = y;
                int u = L[x].x;
                int v = L[x].y;
                if(deep[u] < deep[v]) swap(u,v);
                if(c[x] == ) {
                    pa[u] = finds(v);
                    update(v,u);
                }
            }
        }
}

树链剖分

#include<iostream>
#include<cstring>
#include<cstdio>
#include<cmath>
#include<algorithm>
using namespace std;

#pragma comment(linker, "/STACK:102400000,102400000")

#define ls i<<1
#define rs ls | 1
#define mid ((ll+rr)>>1)
#define root 1,2,n
#define lson ls , ll , mid
#define rson rs , mid + 1 , rr

#define pii pair<int,int>
#define MP make_pair
typedef long long LL;
const long long INF = 1e18+200LL;
const double Pi = acos(-1.0);
const int N = 2e5+, M = 5e5+, inf = 2e9, mod = ;

LL sum[N << ],val[N << ];
int head[N], t = , tot, deep[N], top[N], f[N], siz[N], son[N], pos[N << ];
int n,m;
struct edge{int to,next;LL value;}e[N * ];
struct Line{
    int x,y;LL z;
    Line(int x = , int y = , LL z = ) : x(x), y(y), z(z) {}
}L[N];
void add(int u,int v) {e[t].next=head[u];e[t].to=v;head[u]=t++;}
void dfs1(int u,int fa) {
        siz[u] = ;son[u] = ;
        deep[u] = deep[fa] + ;
        f[u] = fa;
        for(int i = head[u]; i; i = e[i].next) {
            int to = e[i].to;
            if(to == fa) continue;
            dfs1(to,u);
            siz[u] += siz[to];
            if(siz[to] > siz[son[u]]) son[u] = to;
        }
}
void dfs2(int u,int chan) {
        top[u] = son[chan] == u? top[chan] : u;
        pos[u] = ++tot;
        if(son[u]) dfs2(son[u],u);
        for(int i = head[u]; i; i = e[i].next) {
            int to = e[i].to;
            if(to == son[u] || to == chan) continue;
            dfs2(to,u);
        }
}
void push_up(int i) {
    if(log(sum[ls]*1.0) + log(sum[rs] * 1.0) > log(INF * 1.0))
        sum[i] = INF;
    else sum[i] = sum[ls] * sum[rs];
}
void build(int i,int ll,int rr) {
    if(ll == rr) {
        sum[i] = val[ll];
        return ;
    }
    build(lson), build(rson);
    push_up(i);
}
void update(int i,int ll,int rr,int x,LL c)
{
    if(ll == x && rr == x) {
        sum[i] = c;
        return ;
    }
    if(x <= mid) update(lson,x,c);
    else update(rson,x,c);
    push_up(i);
}

LL query(int i,int ll,int rr,int x,int y) {
    if(ll == x && rr == y) return sum[i];
    if(y <= mid) return query(lson,x,y);
    else if(x > mid) return query(rson,x,y);
    else {
        LL fi = query(lson,x,mid);
        LL se = query(rson,mid+,y);
        if(log(fi*1.0) + log(se * 1.0) > log(INF * 1.0)) {
            return INF;
        }
        else return fi*se;
    }
}

LL sub_query(int x,int y,LL res) {
    while(top[x] != top[y]) {
        if(deep[top[x]] < deep[top[y]]) swap(x,y);
       // cout<<pos[top[x]]<<" "<<pos[x]<<endl;
        res /= query(root,pos[top[x]],pos[x]);
        if(res == ) return ;
        x = f[top[x]];
    }
    if(x == y) return res;
    if(deep[x] < deep[y]) swap(x,y);
    // cout<<query(root,pos[y]+1,pos[x])<<endl;
    return res / query(root,pos[y]+,pos[x]);
}

int main () {
        scanf("%d%d",&n,&m);
        for(int i = ; i <= n-; ++i) {
            int a,b;
            LL c;
            scanf("%d%d%I64d",&a,&b,&c);
            add(a,b);
            add(b,a);
            L[i] = Line(a,b,c);
        }
        dfs1(,);
        dfs2(,);
        for(int i = ; i < n; ++i) {
            if(deep[L[i].x] < deep[L[i].y]) swap(L[i].x,L[i].y);
            val[pos[L[i].x]] = L[i].z;
        }
        build(root);
        while(m--) {
                int op,x;
                LL y,z;
                scanf("%d%d%I64d",&op,&x,&y);
                if(op == ) {
                    scanf("%I64d",&z);
                    printf("%I64d\n",sub_query(x,y,z));
                }else {
                    update(root,pos[L[x].x],y);
                }
        }
}