JLOI2016 方

bzoj4558

真是一道非常excited的题目啊…JLOI有毒

题目大意：给一个(N+1)*(M+1)的网格图，格点坐标为(0~N,0~M)，现在挖去了K个点，求剩下多少个正方形（需要注意的是正方形可以是斜着的，多斜都可以）

N,M<=10^6，K<=2*10^3。

首先我们发现有一个非常感人的K=0部分分…

我们考虑K=0怎么做。

对于一个形如这样的正方形，我们叫它(a,b)正方形好了。

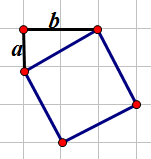
我们可以很容易地发现一个(a,b)正方形实际上要占下(a+b)*(a+b)这么大一块网格。

然后我们考虑a+b的大小，这样a就是[0,a+b]这么大，这样就可以得到一个答案。

代码如下：

现在我们发现，有了这些障碍物，我们只要能求出总共的正方形个数、经过一个障碍点的正方形个数、经过两个障碍点的正方形个数、经过三个点的、经过四个点的即可。

经过三个和经过四个直接二分查找一下显然是trivial的，经过两个点的要考虑是作为边往两侧延伸和作为对角线的情况，也比较trivial。

总共的正方形个数我们已经求出来了，现在我们就要考虑经过某一个障碍点的正方形个数。

对于一个点和它相关的只有四个属性，u,d,l,r对吧。

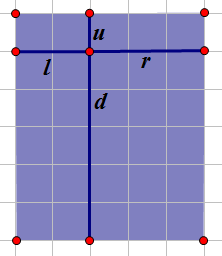
首先我们考虑直的正方形，即(0,x)或(x,0)正方形，因为这类正方形容易被重复统计。

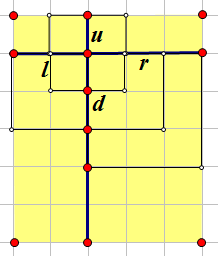
容易发现这类正方形个数为min(u,l)+min(u,r)+min(l,d)+min(d,r)。

其它的正方形显然都是在四个象限中某两个相邻象限的。

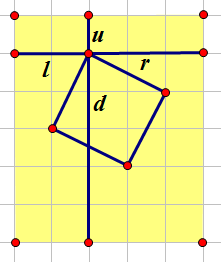
为了简化起见，我们先考虑l,r,d这一象限的。

还是一样，设正方形为(a,b)正方形，我们枚举a+b，假设a+b=c。

因为正方形不是直的，所以a,b≠0。

现在我们考虑求出a的取值范围。

容易发现a<=r，a<=c-1，a>=1，a>=c-l（由于b<=l）。

那么我们可以列出一个形如这样的式子来计算：

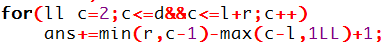
这样显然不够优秀，我们可以人工分类讨论一下…

额其实注意到当r=c-1时c=r+1，当c-l=1时c=l+1，那么min和max的两个“分界点”是l+1和r+1，在分界点中间显然都是一些一次函数，那么就都是等差数列，于是我们就可以避免人工分类讨论了。

有了这个函数calc(l,r,d)，那么calc(u,d,l,r)显然就等于

一些奇怪的细节详见代码…

#include <iostream>
#include <stdio.h>
#include <stdlib.h>
#include <algorithm>
#include <math.h>
using namespace std;
typedef long long ll;
#define MOD 100000007
ll calc(ll l,ll r,ll d)
{
    if(!l||!r||!d) return 0;
    ll ans=0;
    ll upp=min(l+r,d);
    ll ps[3]={l+1,r+1,upp};
    sort(ps,ps+3);
    ll cl=1;
    for(int i=0;i<3;i++)
    {
        ll cr=ps[i];
        if(cr>upp) break;
        if(cr<2||cl==cr) continue;
        ++cl;
        ll vl=min(r,cl-1)-max(cl-l,1LL)+1;
        ll vr=min(r,cr-1)-max(cr-l,1LL)+1;
        ans+=(vl+vr)*(cr-cl+1)/2;
        ans%=MOD;
        cl=cr;
    }
    return ans;
}
ll calc(ll u,ll d,ll l,ll r)
{
    return calc(u,d,l)+calc(u,d,r)+calc(l,r,u)+calc(l,r,d)
          +min(u,r)+min(u,l)+min(d,l)+min(d,r);
}
typedef pair<ll,ll> pll;
pll ps[233333];
#define X first
#define Y second
ll n,m,k,ans=0;
bool ok(pll a)
{
    return a.X>=0&&a.X<n&&a.Y>=0&&a.Y<m;
}
ll tointt(double x)
{
    if(fabs(x-ll(x+0.5))<1e-5) return x+0.5;
    return -1;
}
double chk(double x,double y)
{
    ll xx=tointt(x),yy=tointt(y);
    if(xx>=0&&xx<n&&yy>=0&&yy<m) return 1;
    return 0;
}
int main()
{
    cin>>n>>m>>k; ++n; ++m;
    ll cnt3=0,cnt4=0;
    for(ll g=1;g<=n&&g<=m;g++) ans+=(n-g)%MOD*(m-g)%MOD*g%MOD, ans%=MOD;
    for(int i=1;i<=k;i++)
    {
        ll x,y;
        scanf("%lld%lld",&x,&y);
        ans-=calc(x,n-1-x,y,m-1-y);
        ans%=MOD;
        ps[i]=pll(x,y);
    }
    sort(ps+1,ps+1+k);
    for(int i=1;i<=k;i++)
    {
        for(int j=i+1;j<=k;j++)
        {
            do{
                double mx=(ps[i].X+ps[j].X)/2.0,my=(ps[i].Y+ps[j].Y)/2.0;
                double dx=ps[i].X-mx,dy=ps[i].Y-my;
                if(chk(mx-dy,my+dx)&&chk(mx+dy,my-dx)) ans++;
            }while(0);
            for(int p=-1;p<=1;p+=2)
            {
                ll dx=ps[j].X-ps[i].X,dy=ps[j].Y-ps[i].Y;
                pll n1=pll(ps[j].X-dy*p,ps[j].Y+dx*p);
                pll n2=pll(ps[i].X-dy*p,ps[i].Y+dx*p);
                if(ok(n1)&&ok(n2));else continue;
                ans++;
                int cp=0;
                if(binary_search(ps+1,ps+1+k,n1)) ++cp;
                if(binary_search(ps+1,ps+1+k,n2)) ++cp;
                if(cp==1) cnt3++;
                else if(cp==2) cnt3++, cnt4++;
            }
        }
    }
    ans-=cnt3/2; ans-=cnt4/4;
    printf("%d\n",int(((ans%MOD)+MOD)%MOD));
}