C语言复习---输出魔方阵

一：奇魔方阵

算法：

1.第一个元素放在第一行中间一列

.下一个元素存放在当前元素的上一行、下一列。

.如果上一行、下一列已经有内容，则下一个元素的存放位置为当前列的下一行。

在找上一行、下一行或者下一列的时候，必须把这个矩阵看成是回绕的。

算法实现：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
 
#define MAXSIZE 100
 
int main()
{
    //输出魔方阵
    int n,i,j;
    int row, col;
    int lrow, lcol;    //保存上一步数据，用于还原
    int a[MAXSIZE][MAXSIZE] = {  };
 
    while ()
    {
        printf("print a odd number:(3-99)");
        scanf("%d", &n);
        if (n % )
            break;
    }
 
    row = ;
    col = (n - 1) / 2;  
    a[row][col] = ;
 
    for (i = ; i <= n*n; i++)
    {
        row--;
        col++;
        if (row < )
            row = n - ;
        if (col >= n)
            col = ;
        if (a[row][col])    //若是上一行下一列处有数据了，我们就要将下标还原，行数加一
        {
            row = lrow + ;
            col = lcol;
            if (row >= n)
                row = ;
        }
 
        lcol = col;
        lrow = row;
        a[row][col] = i;
    }
 
    for (i = ; i < n; i++)
    {
        for (j = ; j < n; j++)
            printf("%5d", a[i][j]);
        printf("\n");
    }
 
    system("pause");
    return ;
}

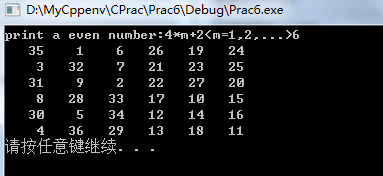
二：阶数n = 4 * m（m =1，2，3……）的偶魔方的规律如下：

按数字从小到大，即1，，……n2顺序对魔方阵从左到右，从上到下进行填充；
将魔方阵分成若干个4×4子方阵，将子方阵对角线上的元素取出；
将取出的元素按从大到小的顺序依次填充到n×n方阵的空缺处。

算法实现：

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
 
#define MAXSIZE 100
 
int main()
{
    //输出魔方阵
    int n,i,j;
    int row, col;
    int a[MAXSIZE][MAXSIZE] = {  };
    int tempArray[MAXSIZE*MAXSIZE / 2] = {  };    //用于存放各个子方阵的主对角线
 
    while ()
    {
        printf("print a even number:(4-100)");
        scanf("%d", &n);
        if (n % ==)
            break;
    }
 
    //步骤一：将数据按顺序填充
    i = ;
    for (row = ; row < n; row++)
        for (col = ; col < n; col++)
            a[row][col] = i++;
 
    //步骤二：将数据全部分为4X4子方阵，取出其中的主对角线，按照大小排序。注意：这里获取的数据已经是从小到大了
    i = ;
    for (row = ; row < n; row++)
    {
        for (col = ; col < n; col++)
        {
            if ((col %  == row % ) || ((col %  + row % ) == ))
            {
                tempArray[i] = a[row][col];
                i++;
            }
        }
    }
 
    //步骤三：将数据从大到小放入之前的子方阵对角线上
    i--;
    for (row = ; row < n; row++)
    {
        for (col = ; col < n; col++)
        {
            if ((col %  == row % ) || ((col %  + row % ) == ))
            {
                a[row][col] = tempArray[i];
                i--;
            }
        }
    }
 
    //步骤四：输出魔方阵
    for (i = ; i < n; i++)
    {
        for (j = ; j < n; j++)
            printf("%5d", a[i][j]);
        printf("\n");
    }
 
    system("pause");
    return ;
}

三：阶数n = 4 * m + 2（m =1，2，3……）的魔方（单偶魔方）

将魔方分成A、B、C、D四个k阶方阵，这四个方阵都为奇方阵，利用上面讲到的方法依次将A、D、B、C填充为奇魔方。
交换A、C魔方元素，对魔方的中间行，交换从中间列向右的m列各对应元素；对其他行，交换从左向右m列各对应元素。
交换B、D魔方元素，交换从中间列向左m – 1列各对应元素。

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
#include <stdlib.h>
#include <math.h>
 
#define MAXSIZE 6
 
int main()
{
    //输出魔方阵
    int n, i, j, k,temp;
    int row, col;
    int lrow, lcol;
    int a[MAXSIZE][MAXSIZE] = {  };
 
    while ()
    {
        printf("print a even number:4*m+2<m=1,2,...>");
        scanf("%d", &n);
        if (n %  == )
            break;
    }
 
    //步骤一：构建四个子方阵ADBC
    //先构建A，然后对A进行每个元素加即可得到所有的子方阵
    k = n / ;
    row = ;
    col = (k - ) / ;
    a[row][col] = ;
    for (i = ; i <= k*k;i++)
    {
        row--;
        col++;
        if (row < )
            row = k - ;
        if (col >= k)
            col = ;
        if (a[row][col])
        {
            row = lrow + ;
            col = lcol;
            if (row >= k)
                row = ;
        }
 
        lcol = col;
        lrow = row;
        a[row][col] = i;
    }
 
    //按照顺序构建DBC方阵
    for (row = ; row < k;row++)
    {
        for (col = ; col < k;col++)
        {
            a[row + k][col + k] = a[row][col] + k*k;    //D子方阵
            a[row][col + k] = a[row][col] + *k*k;    //B子方阵
            a[row + k][col] = a[row][col] + *k*k;    //C子方阵
        }
    }
 
    //步骤二：交换AC子方阵的数据
    //1.先交换中间行的右半部分的m列，N=2*(2*m+1),k=2*m+1,m=(k-1)/2,所以这里的m是不包含最后一列的，包含中间列
    //2.对于其他行，将会每行的前半部分
    for (row = ; row < k;row++)
    {
        if (row == k / )    //中间行
        {
            for (col = k / ; col < k - ; col++)
            {
                temp = a[row][col];
                a[row][col] = a[row + k][col];
                a[row + k][col] = temp;
            }
        }
        else   //其他行，交换前m列，不包含中间列
        {
            for (col = ; col < k / ;col++)
            {
                temp = a[row][col];
                a[row][col] = a[row + k][col];
                a[row + k][col] = temp;
            }
        }
    }
 
    //步骤三：交换BD子方阵，交换中间列向左m-1列
    for (row = ; row < k;row++)
    {
        for (i = ; i < (k - ) /  - ; i++)
        {
            temp = a[row][k + k /  - i];
            a[row][k + k /  - i] = a[row + k][k + k /  - i];
            a[row + k][k + k /  - i] = temp;
        }
    }
 
    //步骤四：输出魔方阵
    for (i = ; i < n; i++)
    {
        for (j = ; j < n; j++)
            printf("%5d", a[i][j]);
        printf("\n");
    }
 
    system("pause");
    return ;
}