L3-021 神坛 （30 分) 计算几何

　　

在古老的迈瑞城，巍然屹立着 n 块神石。长老们商议，选取 3 块神石围成一个神坛。因为神坛的能量强度与它的面积成反比，因此神坛的面积越小越好。特殊地，如果有两块神石坐标相同，或者三块神石共线，神坛的面积为 0.000。

长老们发现这个问题没有那么简单，于是委托你编程解决这个难题。

输入格式：

输入在第一行给出一个正整数 n（3 ≤ n ≤ 5000）。随后 n 行，每行有两个整数，分别表示神石的横坐标、纵坐标（− 横坐标、纵坐标 <）。

输出格式：

在一行中输出神坛的最小面积，四舍五入保留 3 位小数。

输入样例：

8
3 4
2 4
1 1
4 1
0 3
3 0
1 3
4 2

输出样例：

0.500

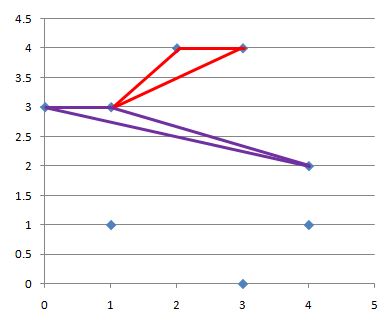
样例解释

输出的数值等于图中红色或紫色框线的三角形的面积。

第一次接触计算几何的题目

先算出两两边的向量  再把向量按照极角来排序    然后用叉乘法一一求面积 更新最小值

#include<bits/stdc++.h>
using namespace std;
//input by bxd
#define rep(i,a,b) for(int i=(a);i<=(b);i++)
#define repp(i,a,b) for(int i=(a);i>=(b);i--)
#define RI(n) scanf("%d",&(n))
#define RII(n,m) scanf("%d%d",&n,&m)
#define RIII(n,m,k) scanf("%d%d%d",&n,&m,&k)
#define RS(s) scanf("%s",s);
#define LL long long
#define pb push_back
#define fi first
#define REP(i,N)  for(int i=0;i<(N);i++)
#define CLR(A,v)  memset(A,v,sizeof A)
///////////////////////////////////
#define inf 0x3f3f3f3f
#define N 50010
int n;

struct node{
    long long x,y;
}p[N],temp[N];
bool cmp(node a,node b) {
    return b.y*a.x>a.y*b.x;
}
int main() {
    scanf("%d",&n);
    for(int i=;i<=n;i++) {
        scanf("%lld %lld",&p[i].x,&p[i].y);
    }
    double ans=pow(,)/;
    for(int i=;i<=n;i++) {
        int t=;
        for(int j=;j<=n;j++) {
            if(i==j) continue;
            temp[t].x=p[j].x-p[i].x;
            temp[t].y=p[j].y-p[i].y;
            t++;
        }
        sort(temp+,temp+t,cmp);
        for(int j=;j<t-;j++){
        ans=min(ans,(temp[j].x*temp[j+].y-temp[j+].x*temp[j].y)*0.5);
        }
    }
    printf("%.3f",ans);
    return ;
}