李宏毅机器学习笔记4：Brief Introduction of Deep Learning、Backpropagation(后向传播算法)

李宏毅老师的机器学习课程和吴恩达老师的机器学习课程都是都是ML和DL非常好的入门资料，在YouTube、网易云课堂、B站都能观看到相应的课程视频，接下来这一系列的博客我都将记录老师上课的笔记以及自己对这些知识内容的理解与补充。(本笔记配合李宏毅老师的视频一起使用效果更佳！）

---

Lecture 6: Brief Introduction of Deep Learning

本节课主要围绕Deep Learing三步骤：

（1）function set

（2）goodness of function

（3）pick the best function

1.function set

Neuron之间采用不同的连接方式，就会得到不同的网络结构。

给定了网络结构，就定义了一个function set。

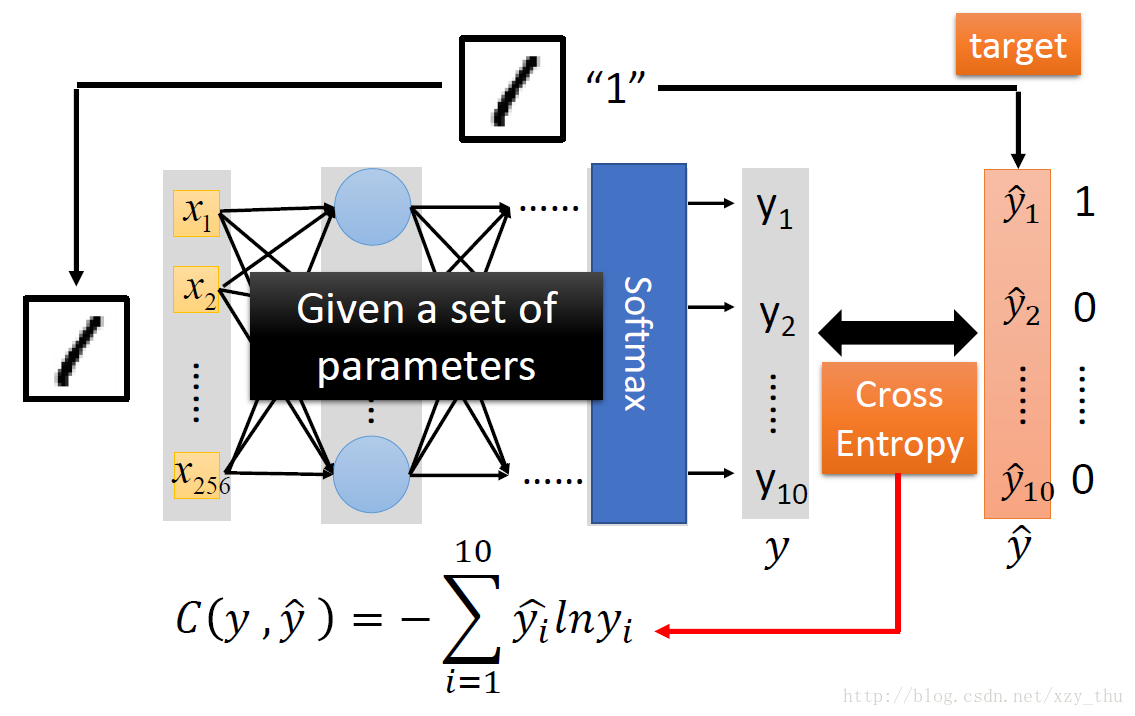
给定了网络结构并给定了参数，网络就是一个函数：而输入输出的形式都是向量。如下图所示：

在output layer之前的部分，可以看做特征提取(上一节描述的概念)。output layer是Multi-class Classifier.

但是问题来了，Deep learning中的隐层到底要订多少层合适呢？

2.goodness of function

损失函数表达式以及优化过程如下所示：

3.pick the best function

显而易见，优化损失函数采用的依旧是Gradient Descent。

但是现在市面上有很多软件可以帮我们进行GD的大部分计算：

Backpropagation:后向传播算法，在下一节内容我们将会详细讨论。

Lecture 7: Backpropagation

在神经网络的计算中，神经网络通常含有非常深的隐藏层，换句话说就是可能拥有百万量级的参数，为了在梯度下降时更加有效地计算梯度，所以本节课引入一个概念：反向传播算法(Backpropagation)

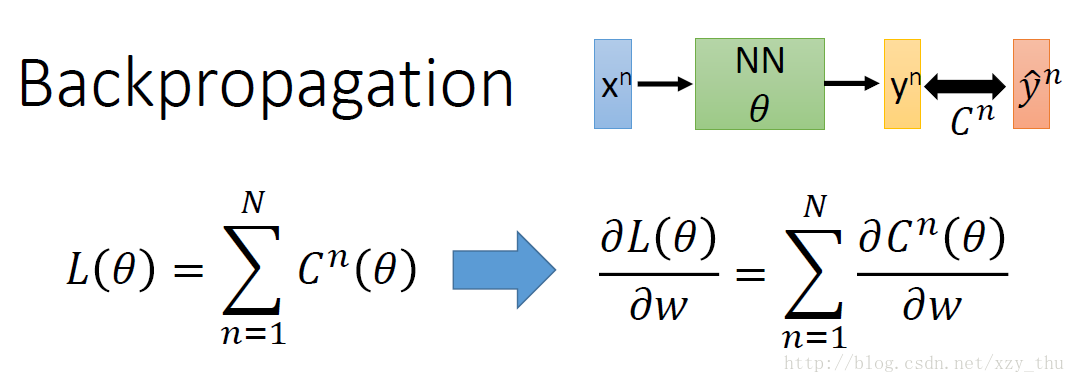
先让我们考虑只有一组data的时候对参数的偏微分，如下图：

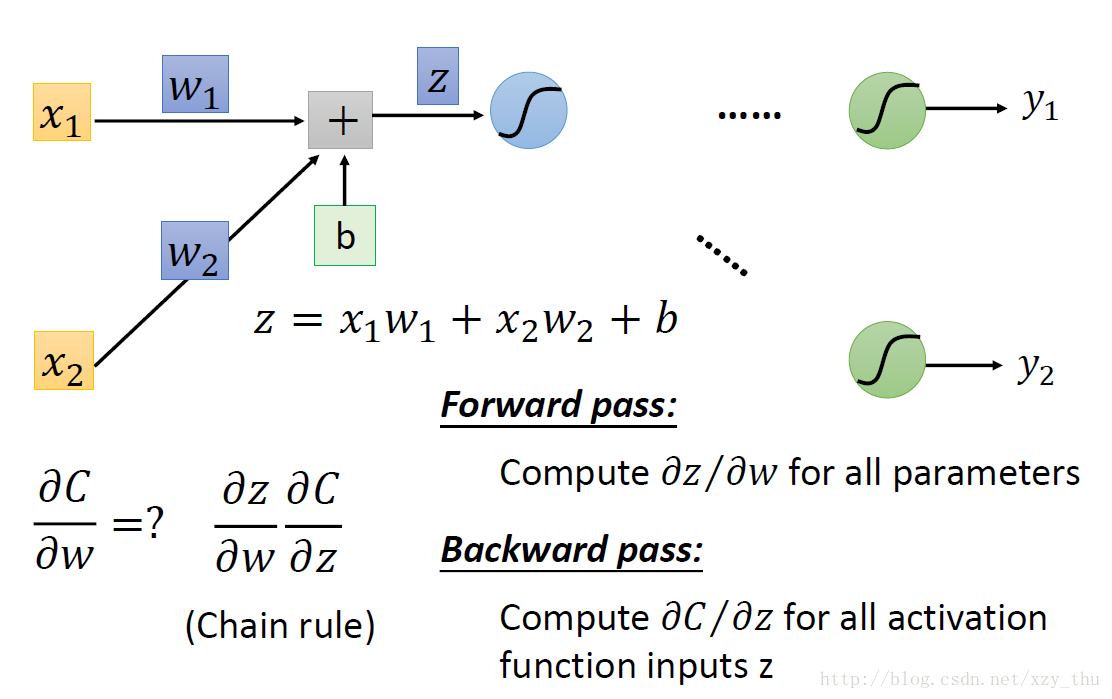
根据链式法则， ∂C/∂w = ∂z/∂w * ∂C/∂z，计算∂z/∂w我们称为前向过程，计算∂C/∂z我们称为后向过程

前向过程：从上图中，我们能明显看出前向过程∂z/∂w的值。∂z / ∂wi = the value connected by the weight wi。

有关后向过程，让我们一起看下图：

后向过程：根据链式法则， ∂C / ∂z = ∂a / ∂z * ∂C / ∂a，其中∂a / ∂z = σ′(z)。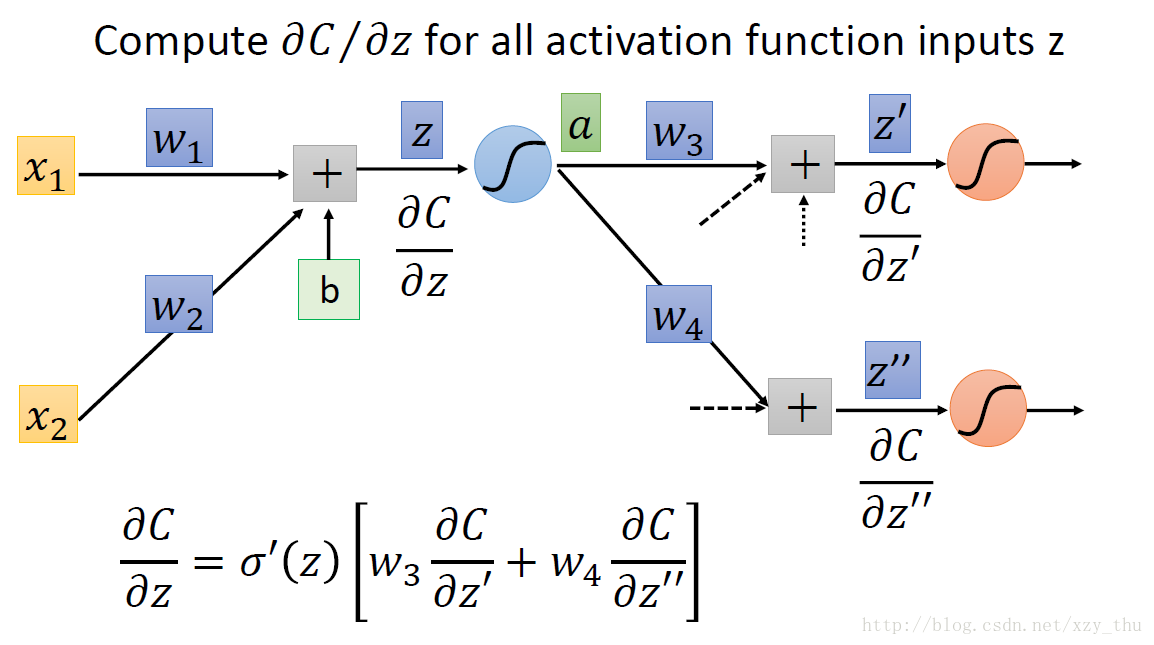

如下图所示倘若我们从另外一个观点看待上面的式子：有另外一个neuron（下图中的三角形，表示乘法/放大器），input是∂C / ∂z′与∂C / ∂z′′，权重分别是w3,w4w3,w4，求和经过neuron(乘以σ′(z)),得到∂C / ∂z。

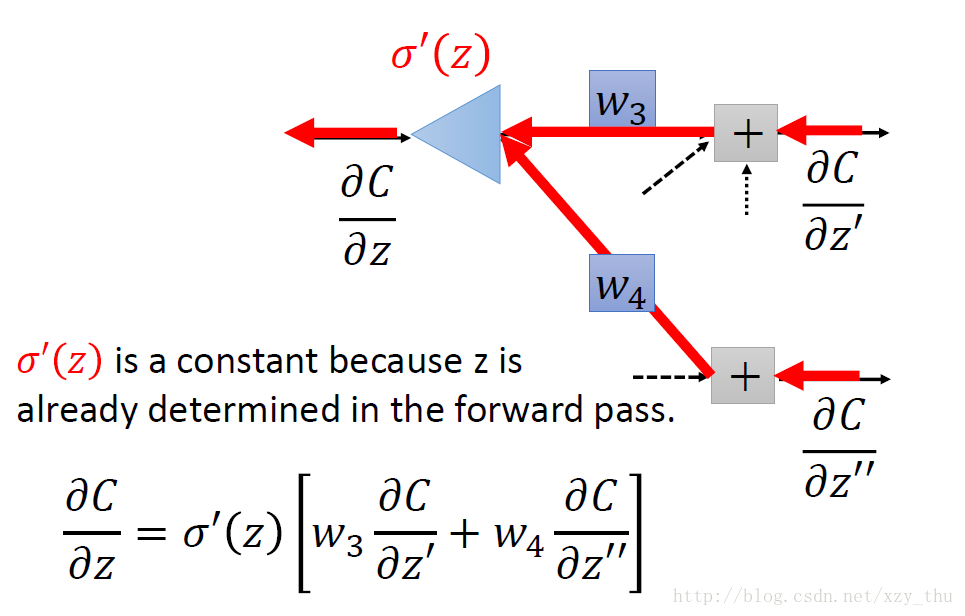
那么现在问题又来了，我们该如何计算∂C / ∂z′与∂C / ∂z′′呢？分两种情况

（1）z′,z″ 所接的neuron是output layer的neuron

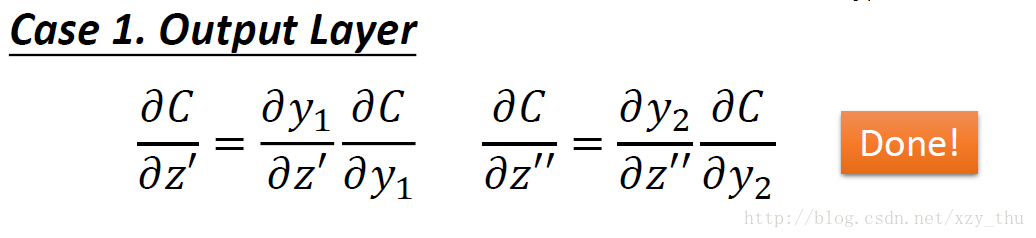
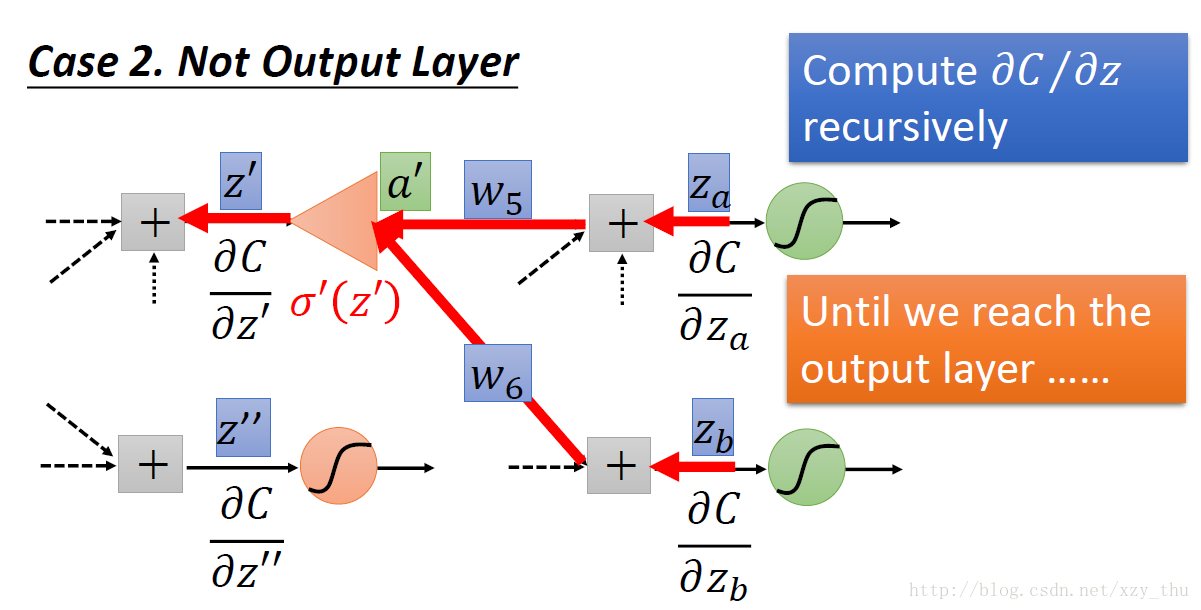
（2）z′,z″ 所接的neuron不是output layer的neuron

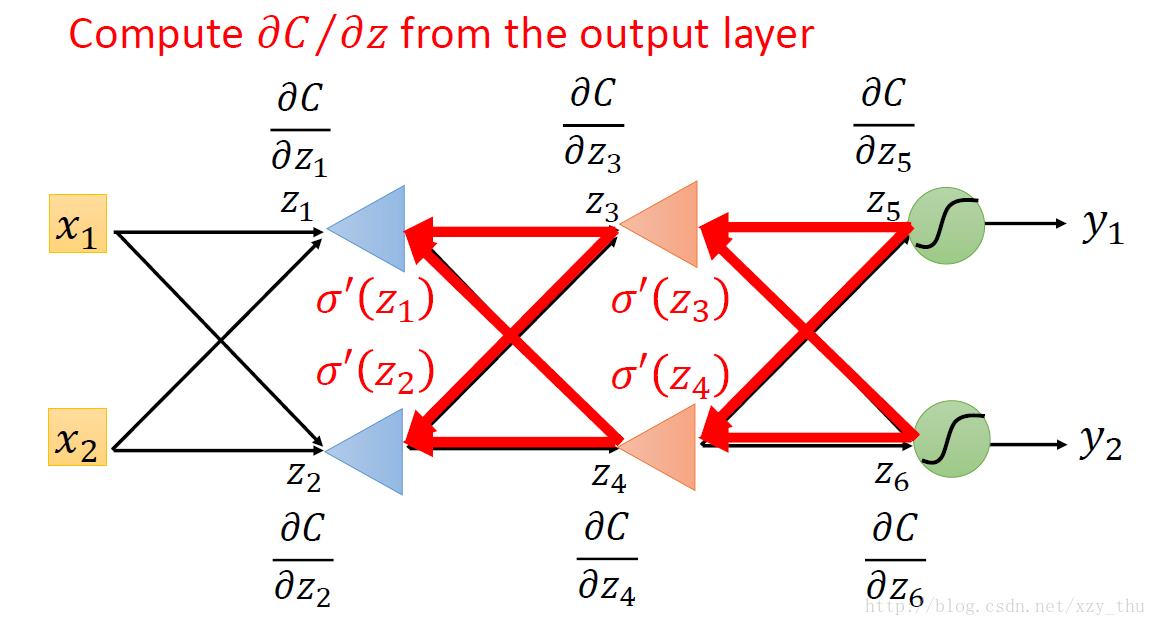
总结：实际上在做Backword Pass的时候，就是建立一个反向的neural network的过程，对损失函数求导 = 前向传播 * 后向传播：

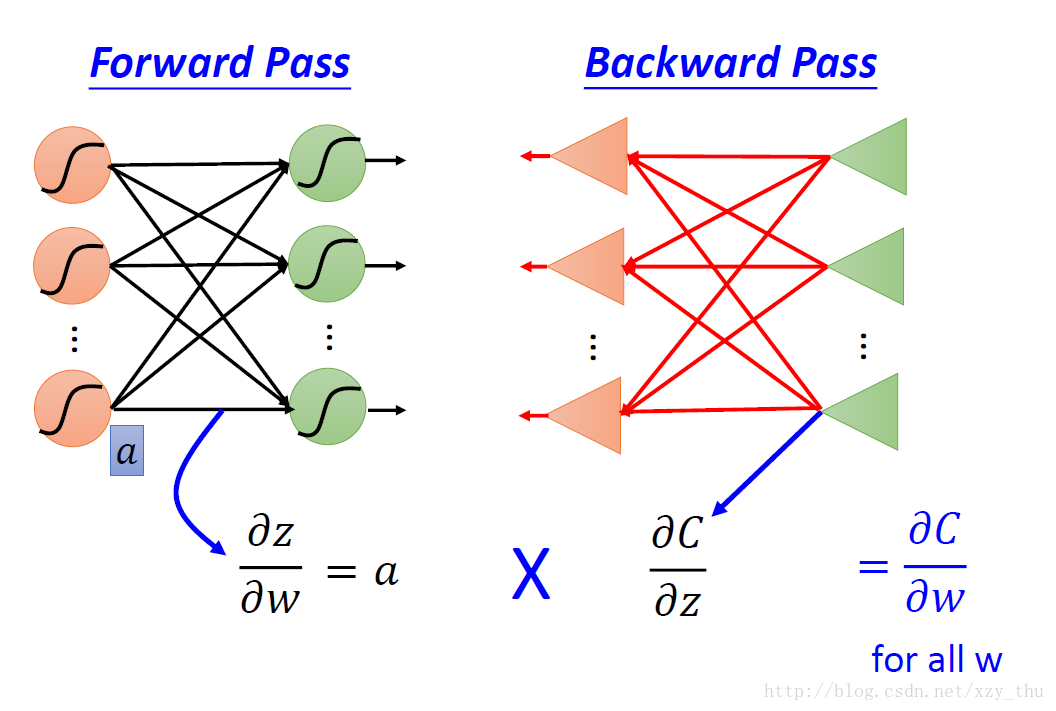
划重点：

链式法则将计算∂C / ∂w 拆成前向过程与后向过程。

前向过程计算的是∂z / ∂w ，这里z是w所指neuron的input，计算结果是与w相连的值。

后向过程计算的是∂C / ∂z，这里z仍是w所指neuron的input，计算结果通过从后至前递归得到