BZOJ3512 DZY Loves Math IV

解：这又是什么神仙毒瘤题......

我直接把后面那个phi用phi * I = id反演一波，得到个式子，然后推不动了......

实际上第一步我就大错特错了。考虑到n很小，我们有

然后计算S，我们根据欧拉函数的性质有：

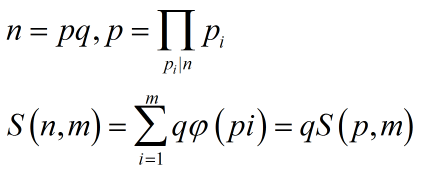
于是只考虑n sqr free的情况。

到这里有两种解法，一种是暴力递归。

考虑n的一个因子p，我们先提取出前面那一项，但是这还不够。因为当p|i的时候应该提出来p = phi[p] + 1。

于是我们在后面补上。令i = pt，就有了递归式。

 #include <cstdio>
 #include <map>

 typedef long long LL;
 const int N = , T = ;
 const LL MO = 1e9 + , INF = 0x7f7f7f7f7f7f7f7fll;

 int phi[N], p[N], top, last[N];
 LL Phi[N], inv2;
 bool vis[N];

 namespace Hash {
     struct Node {
         LL val, ans;
         int nex;
         Node(LL x = , LL y = , int z = ) {
             val = x;
             ans = y;
             nex = z;
         }
     }node[]; int top;
     const int mod = ;
     int e[mod];
     inline void insert(LL p, LL v) {
         int x = p % mod;
         node[++top] = Node(p, v, e[x]);
         e[x] = top;
         return;
     }
     inline LL find(LL p) {
         int x = p % mod;
         for(int i = e[x]; i; i = node[i].nex) {
             if(node[i].val == p) return node[i].ans;
         }
         return -INF;
     }
 }

 inline void getp(int n) {
     phi[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             phi[i] = i - ;
             last[i] = i;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             last[i * p[j]] = p[j];
             if(i % p[j] == ) {
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
         }
     }
     for(int i = ; i <= n; i++) {
         Phi[i] = (Phi[i - ] + phi[i]) % MO;
     }
     return;
 }

 LL getPhi(LL x) {
     if(x <= ) return ;
     if(x <= T) return Phi[x];
     LL temp = Hash::find(x);
     if(temp != -INF) return temp;
     //printf("getPhi %lld T = %d\n", x, T);
     LL ans = (x % MO) * ((x + ) % MO) % MO * inv2 % MO;
     for(LL i = , j; i <= x; i = j + ) {
         j = x / (x / i);
         ans -= ((j - i + ) % MO) * getPhi(x / i) % MO;
         ans = (ans % MO + MO) % MO;
     }
     Hash::insert(x, ans);
     return ans;
 }

 LL S(LL n, LL m) {
     //printf("S : %lld %lld \n", n, m);
     if(n == ) return getPhi(m);
     if(m == ) return ;
     if(m == ) return phi[n];
     LL p = last[n];
     LL ans = (phi[p] * S(n / p, m) % MO + S(n, m / p)) % MO;
     return ans;
 }

 int main() {
     inv2 = (MO + ) / ;
     getp(T);
     LL nn, m;
     scanf("%lld%lld", &nn, &m);
     LL ans = ;
     for(int i = ; i <= nn; i++) {
         LL p = , q = , n = i;
         while(n > ) {
             LL temp = last[n];
             p *= temp;
             n /= temp;
             while(n % temp == ) {
                 n /= temp;
                 q *= temp;
             }
         }
         ans = (ans + q * S(p, m) % MO) % MO;
     }
     printf("%lld\n", ans);
     return ;
 }

TLE

还有一种继续推：

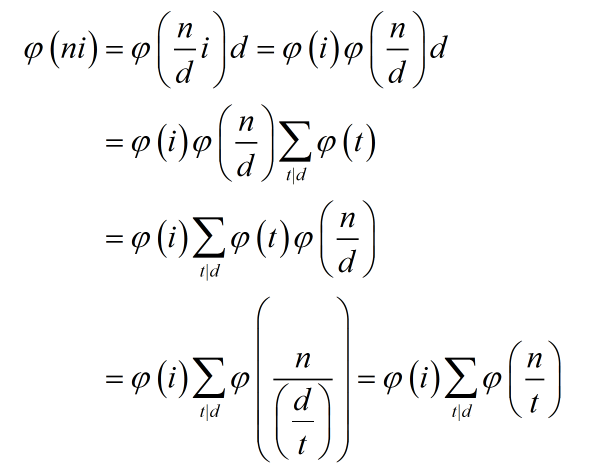
其中d = gcd(i,n)

有个关键点是n是sqr free...否则一直想不明白。

接下来把这个式子带入S的定义式中。

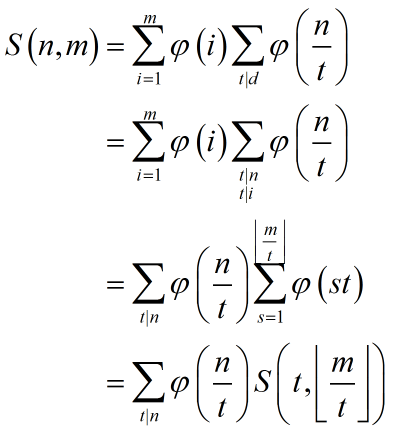
这样就可以递归了。

注意......这个S也可以记忆化的，否则死活过不去。用map。

 #include <cstdio>
 #include <map>

 typedef long long LL;
 const int N = , T = ;
 const LL MO = 1e9 + , INF = 0x7f7f7f7f7f7f7f7fll;

 int p[N], last[N], top, phi[N];
 LL Phi[N], inv2;
 bool vis[N];

 std::map<LL, LL> mp[], Hash;

 inline void getp(int n) {
     phi[] = ;
     for(int i = ; i <= n; i++) {
         if(!vis[i]) {
             p[++top] = i;
             phi[i] = i - ;
             last[i] = i;
         }
         for(int j = ; j <= top && i * p[j] <= n; j++) {
             vis[i * p[j]] = ;
             last[i * p[j]] = p[j];
             if(i % p[j] == ) {
                 phi[i * p[j]] = phi[i] * p[j];
                 break;
             }
             phi[i * p[j]] = phi[i] * (p[j] - );
         }
     }
     for(int i = ; i <= n; i++) {
         Phi[i] = (Phi[i - ] + phi[i]) % MO;
     }
     return;
 }

 LL getPhi(LL x) {
     if(x <= ) return ;
     if(x <= T) return Phi[x];
     if(Hash.count(x)) return Hash[x];
     //printf("Phi %lld \n", x);
     LL ans = (x % MO) * ((x + ) % MO) % MO * inv2 % MO;
     for(LL i = , j; i <= x; i = j + ) {
         j = x / (x / i);
         ans -= ((j - i + ) % MO) * getPhi(x / i) % MO;
         ans = (ans % MO + MO) % MO;
     }
     return Hash[x] = ans;
 }

 LL S(int n, LL m) {
     //printf("S %d %lld \n", n, m);
     if(n == ) return getPhi(m);
     if(m == ) return phi[n];
     if(m == ) return ;
     if(mp[n][m]) return mp[n][m];
     LL ans = ;
     for(int i = ; i * i <= n; i++) {
         if(n % i) continue;
         ans += phi[n / i] * S(i, m / i) % MO;
         if(i * i < n) {
             ans += phi[i] * S(n / i, m / (n / i)) % MO;
         }
         ans = (ans % MO + MO) % MO;
     }
     return mp[n][m] = ans;
 }

 int main() {
     inv2 = (MO + ) / ;
     int nn; LL m;
     getp(T);
     scanf("%d%lld", &nn, &m);
     LL ans = ;
     for(int i = ; i <= nn; i++) {
         int n = i, p = , q = ;
         //printf("i = %d \n", i);
         while(n > ) {
             int temp = last[n];
             n /= temp;
             p *= temp;
             while(n % temp == ) {
                 n /= temp;
                 q *= temp;
             }
         }
         ans += q * S(p, m) % MO;
         ans = (ans % MO + MO) % MO;
     }
     printf("%lld\n", ans);
     return ;
 }

AC代码

这个时间到底是怎么算的啊......玄学。