空间点绕轴旋转公式&程序(C++)

关键词：空间旋转、旋转轴

用途：相机位姿估计、无人机位姿估计、3D游戏、3D建模

文章类型：概念、公式总结（本文不带推导过程，若想了解公式是如何推出来的请搜索文献），C++函数展示

@Author：VShawn(singlex@foxmail.com)

@Date:2016-11-04

@Lab: CvLab202@CSU

写在前面的一些概念

右手系

关于这个概念，搞3D的人应该都懂，而像我这样做图像处理的可能就对这个知道的比较少了。右手系这个概念其实很简单，看图就懂了。在坐标系中，右手摆成下图的样子，当拇指指向X轴食指指向Y轴时，中指指向了Z轴，满足这个条件的坐标系就是右手系。本文所有概念都在右手系下进行讨论。

右手系

旋转90°到底是怎么转

当我要让一个点，绕Y轴转动了90°，并且用程序计算出了旋转结果，为了验证这个点是否旋转正确，我们需要知道这个90°是怎么转的。在网上搜索了挺多文章，都没有对这个东西进行明确的定义，那么这里给出我的总结。从原点（0,0,0）往Y轴方向看，此时视野中的坐标系降维到二维坐标系XOZ，那么让点绕O点顺时针转90°，即为正确的旋转结果。

[图待补]

问题一：XYZ空间内某点绕X、Y、Z轴旋转一次

这个问题比较简单，网上已经有较多总结：

设旋转前坐标为，旋转后坐标为。

1.绕Z轴旋转γ角

首先给出向量表示：

\[\left[ x',y',z',1 \right]=\left[ x,y,z,1 \right]\left[ \begin{matrix} \cos \gamma & \sin \gamma & 0 & 0 \\ -\sin \gamma & \cos \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\\end{matrix} \right]\]

然后是公式表示：

\[\begin{align} & x'=cos\gamma \cdot x-sin\gamma \cdot y \\ & y'=\sin \gamma \cdot x+co\gamma \cdot y \\ & z'=z \\ \end{align}\]

最后是代码表示

//将空间点绕Z轴旋转
//输入参数 x y为空间点原始x y坐标
//thetaz为空间点绕Z轴旋转多少度，角度制范围在-180到180
//outx outy为旋转后的结果坐标
void codeRotateByZ(double x, double y, double thetaz, double& outx, double& outy)
{
    double x1 = x;//将变量拷贝一次，保证&x == &outx这种情况下也能计算正确
    double y1 = y;
    double rz = thetaz * CV_PI / 180;
    outx = cos(rz) * x1 - sin(rz) * y1;
    outy = sin(rz) * x1 + cos(rz) * y1;

}

2.绕Y轴旋转β角

首先给出向量表示：

\[\left[ x',y',z',1 \right]=\left[ x,y,z,1 \right]\left[ \begin{matrix} \cos \beta & 0 & -\sin \beta & 0 \\ 0 & 1 & 0 & 0 \\ \sin \beta & 0 & \cos \beta & 0 \\ 0 & 0 & 0 & 1 \\\end{matrix} \right]\]

然后是公式表示：

\[\begin{align} & x'=cos\beta \cdot x+sin\beta \cdot z \\ & y'=y \\ & z'=-\sin \beta \cdot x+\cos \beta \cdot z \\ \end{align}\]

最后是代码表示

//将空间点绕Y轴旋转
//输入参数 x z为空间点原始x z坐标
//thetay为空间点绕Y轴旋转多少度，角度制范围在-180到180
//outx outz为旋转后的结果坐标
void codeRotateByY(double x, double z, double thetay, double& outx, double& outz)
{
    double x1 = x;
    double z1 = z;
    double ry = thetay * CV_PI / 180;
    outx = cos(ry) * x1 + sin(ry) * z1;
    outz = cos(ry) * z1 - sin(ry) * x1;
}

　　

3.绕X轴旋转α角

首先给出向量表示：

\[\left[ x',y',z',1 \right]=\left[ x,y,z,1 \right]\left[ \begin{matrix} 1 & 0 & 0 & 0 \\ 0 & \cos \alpha & \sin \alpha & 0 \\ 0 & -\sin \alpha & \cos \alpha & 0 \\ 0 & 0 & 0 & 1 \\\end{matrix} \right]\]

然后是公式表示：

\[\begin{align} & x'=x \\ & y'=\cos \alpha \cdot y-\sin \alpha \cdot z \\ & z'=\sin \alpha \cdot y+\sin \alpha \cdot z \\ \end{align}\]

最后是代码表示

//将空间点绕X轴旋转
//输入参数 y z为空间点原始y z坐标
//thetax为空间点绕X轴旋转多少度，角度制范围在-180到180
//outy outz为旋转后的结果坐标
void codeRotateByX(double y, double z, double thetax, double& outy, double& outz)
{
	double y1 = y;//将变量拷贝一次，保证&y == &y这种情况下也能计算正确
	double z1 = z;
	double rx = thetax * CV_PI / 180;
	outy = cos(rx) * y1 - sin(rx) * z1;
	outz = cos(rx) * z1 + sin(rx) * y1;
}

　　

问题二：空间点绕任意轴旋转

首先，需要定义"任意轴"的单位向量，例如X轴可以用向量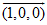来表示。

那么假设旋转轴的单位向量为，旋转前坐标为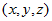，旋转后坐标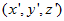为，旋转角为，于是有：

\[\begin{align} & x'=(vx\cdot vx\cdot (1-cos\theta )+cos\theta )\cdot x+(vx\cdot vy\cdot (1-cos\theta )-vz\cdot sin\theta )\cdot y+(vx\cdot vz\cdot (1-cos\theta )+vy\cdot sin\theta )\cdot z \\ & y'=(vx\cdot vy\cdot (1-cos\theta )+vz\cdot sin\theta )\cdot x+(vy\cdot vy\cdot (1-cos\theta )+cos\theta )\cdot y+(vy\cdot vz\cdot (1-cos\theta )-vx\cdot sin\theta )\cdot z \\ & z'=(vx\cdot vz\cdot (1-\cos \theta )-vy\cdot \sin \theta )\cdot x+(vy\cdot vz\cdot (1-\cos \theta )+vx\cdot \sin \theta )\cdot y+(vz\cdot vz\cdot (1-\cos \theta )+\cos \theta )\cdot z \\ \end{align}\]

计算时照着公式代入即可。

最后给出代码实现：

//定义返回结构体
struct Point3f
{
	Point3f(double _x, double _y, double _z)
	{
		x = _x;
		y = _y;
		z = _z;
	}
	double x;
	double y;
	double z;
};

//点绕任意向量旋转，右手系
//输入参数old_x，old_y，old_z为旋转前空间点的坐标
//vx，vy，vz为旋转轴向量
//theta为旋转角度角度制，范围在-180到180
//返回值为旋转后坐标点
Point3f RotateByVector(double old_x, double old_y, double old_z, double vx, double vy, double vz, double theta)
{
	double r = theta * CV_PI / 180;
	double c = cos(r);
	double s = sin(r);
	double new_x = (vx*vx*(1 - c) + c) * old_x + (vx*vy*(1 - c) - vz*s) * old_y + (vx*vz*(1 - c) + vy*s) * old_z;
	double new_y = (vy*vx*(1 - c) + vz*s) * old_x + (vy*vy*(1 - c) + c) * old_y + (vy*vz*(1 - c) - vx*s) * old_z;
	double new_z = (vx*vz*(1 - c) - vy*s) * old_x + (vy*vz*(1 - c) + vx*s) * old_y + (vz*vz*(1 - c) + c) * old_z;
	return Point3f(new_x, new_y, new_z);
}

　

问题三：空间点绕xyz轴连续旋转

前面的问题比较基础，到这个问题就需要一点空间想象力了。

首先我假设一个点绕x、y、z轴旋转90°，最终它会落在哪里？这个答案不是唯一的，因为旋转的顺序将会影响到最终的结果。

以点(1,2,3)为例

A 我让它首先绕x轴转90°，再绕y轴转90°，再绕z轴转90°。

double x = 1, y = 2, z = 3;
codeRotateByX(y, z, 90, y, z);
codeRotateByY(x, z, -90, x, z);
codeRotateByZ(x, y, -90, x, y);
cout << endl << "   (1,2,3) -> (" << x << ',' << y << ',' << z << ")" << endl << endl;

旋转结果是：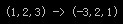

B 这一次我让它首先绕z轴转90°，再绕y轴转90°，最后绕z轴转90°。

double x = 1, y = 2, z = 3;
codeRotateByZ(x, y, -90, x, y);
codeRotateByY(x, z, -90, x, z);
codeRotateByX(y, z, 90, y, z);
cout << endl << "   (1,2,3) -> (" << x << ',' << y << ',' << z << ")" << endl << endl;

这次的结果是：

显然，不同的旋转顺序导致了结果的不同，因此在处理空间内绕轴旋转的问题时，我们需要严格定义每次旋转的顺序，否则会导致错误的答案。