1.为什么要有平衡二叉树?

　　上一节我们讲了一般的二叉查找树, 其期望深度为O(log2n), 其各操作的时间复杂度O(log2n)同时也是由此决定的.但是在某些情况下(如在插入的序列是有序的时候), 二叉查找树就会退化成近似链或链.如下图(b). 此时, 其操作的时间复杂度退化成线性的,即O(n).我们可以通过随机化建立二叉搜索树来尽量的避免这种情况，但是在进行了多次的操作之后，由于在删除时，我们总是选择将待删除节点的后继代替它本身，这样就会造成总是右边的节点数目减少，以至于树向左偏沉。这同时也会造成树的平衡性受到破坏，降低它的操作的时间复杂度。

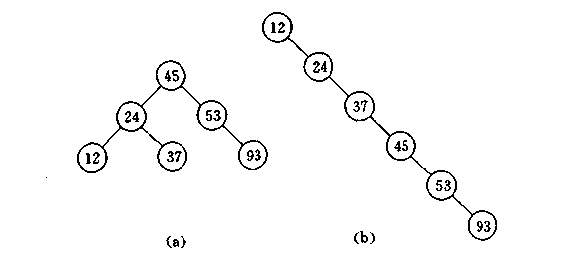
　　因此, 阿德尔森-维尔斯和兰迪斯(Adelson-Velskii and Landis)于1962年首先提出平衡二叉树.平衡二叉树具有如下性质:

平衡二叉树或为空树,或为如下性质的二叉查找树:

（1）左右子树深度之差的绝对值不超过1;

（2）左右子树仍然为平衡二叉树.

　　在平衡二叉树中，其高度一般都良好地维持在O（log2n），大大降低了操作的时间复杂度。

2.平衡二叉树旋转操作

3.AVL树

(4) 二叉平衡树, AVL树的更多相关文章

  1. Algorithms: 二叉平衡树(AVL)

    二叉平衡树(AVL):   这个数据结构我在三月份学数据结构结构的时候遇到过.但当时没调通.也就没写下来.前几天要用的时候给调好了!详细AVL是什么,我就不介绍了,维基百科都有.  后面两月又要忙了. ...

  2. 树-二叉搜索树-AVL树

    树-二叉搜索树-AVL树 树 树的基本概念 节点的度:节点的儿子数 树的度:Max{节点的度} 节点的高度:节点到各叶节点的最大路径长度 树的高度:根节点的高度 节点的深度(层数):根节点到该节点的路 ...

  3. 二叉平衡树AVL的插入与删除(java实现)

    二叉平衡树 全图基础解释参考链接:http://btechsmartclass.com/data_structures/avl-trees.html 二叉平衡树:https://www.cnblogs ...

  4. 树-二叉平衡树AVL

    基本概念 AVL树:树中任何节点的两个子树的高度最大差别为1. AVL树的查找.插入和删除在平均和最坏情况下都是O(logn). AVL实现 AVL树的节点包括的几个组成对象: (01) key -- ...

  5. 高度平衡的二叉搜索树(AVL树)

    AVL树的基本概念 AVL树是一种高度平衡的(height balanced)二叉搜索树:对每一个结点x,x的左子树与右子树的高度差(平衡因子)至多为1. 有人也许要问:为什么要有AVL树呢?它有什么 ...

  6. 各种查找算法的选用分析（顺序查找、二分查找、二叉平衡树、B树、红黑树、B+树）

    目录 顺序查找 二分查找 二叉平衡树 B树 红黑树 B+树 参考文档 顺序查找 给你一组数,最自然的效率最低的查找算法是顺序查找--从头到尾挨个挨个遍历查找,它的时间复杂度为O(n). 二分查找 而另 ...

  7. java项目---用java实现二叉平衡树（AVL树）并打印结果（详）(3星)

    package Demo; public class AVLtree { private Node root; //首先定义根节点 private static class Node{ //定义Nod ...

  8. AVL树(二叉平衡树)详解与实现

    AVL树概念 前面学习二叉查找树和二叉树的各种遍历,但是其查找效率不稳定(斜树),而二叉平衡树的用途更多.查找相比稳定很多.(欢迎关注数据结构专栏) AVL树是带有平衡条件的二叉查找树.这个平衡条件必 ...

  9. 从零开始学算法---二叉平衡树（AVL树）

    先来了解一些基本概念: 1)什么是二叉平衡树? 之前我们了解过二叉查找树,我们说通常来讲, 对于一棵有n个节点的二叉查找树,查询一个节点的时间复杂度为log以2为底的N的对数. 通常来讲是这样的, 但 ...

随机推荐

  1. Ant 学习及常用任务

    安装与配置 下载地址:http://ant.apache.org/bindownload.cgi,解压. 添加系统环境变量: ANT_HOME,该变量指向Ant解压后的根目录. PATH,追加path ...

  2. fullpage 插件学习心得

    fullpage.js 是一个基于jquery 的插件,它能够轻松的制作出高大上的全屏网站,主要功能有; 1．支持鼠标滚动 2．支持前进后退和键盘控制 3．多个回调函数 4．支持 CSS3 动画 5． ...

  3. CSS元素居中的常用方法

    只有普通流和绝对定位的元素可以设置居中,浮动元素是不存在居中的. 1.块级元素居中 1) 普通流元素(position : static 或 position : relative) 水平居中:{ m ...

  4. error: RPC failed; result=22, HTTP code = 411

    git config http.postBuffer 524288000orgit config --system http.postBuffer 524288000  

  5. Java 多线程之单例设计模式

    转载:https://segmentfault.com/a/1190000007504892 概念: Java中单例模式是一种常见的设计模式,单例模式的写法有好几种,这里主要介绍两种:懒汉式单例.饿汉 ...

  6. 谁也无法挡住我访问Google---使用Nginx反向代理攻略

    展示最终成果: 浏览器打开​ http://www.manda13.com/(慢搭搜索)这个是自己搭建的百度网盘搜索,欢迎测试 点击右上角“原版Google”,就可以访问Google. 是不是很方便. ...

  7. STL—Vector简介

    有关C++ STL 中的vector向量的用法(代码示例) 一. 简介 Vector是一个称为向量的顺序容器(不明白顺序容器与关联容器的可以Google). 二. 特点 1. 动态(相当于一个动态数组 ...

  8. 9款一键快速搭建PHP运行环境的好工具

    9款一键快速搭建PHP运行环境的好工具 胡倡萌 2011/02/19 网络资源 77,063 1     内容提要: 建立一个PHP网站,首先需要搭建PHP的开发和运行环境,对于PHP初学者也是一个难 ...

  9. JS的window.onload与JQuery的$(document).ready(function(){})的区别

    前段时间去面试被问及JS的加载(onload)与jQuery中加载(ready)方法的区别,瞬时懵逼了,关于这个知识点平时还真没怎么注意. 最近先来无事便查了一下资料, onload 事件(W3c上给 ...

  10. switch 与 python字典

    python 中并没有switch语句,但是有一个数据类型与switch语句特别相似,它就是 dict{ key: value, ...} 下面用 dict{ key:value,..} 来简单的实现 ...