EM算法（2）：GMM训练算法

目录

EM算法（1）：K-means 算法

EM算法（2）：GMM训练算法

EM算法（3）：EM算法运用

EM算法（4）：EM算法证明

　　　　　　　　　　　　　　　　EM算法（2）：GMM训练算法

1. 简介

　　GMM模型全称为Gaussian Mixture Model，即高斯混合模型。其主要是针对普通的单个高斯模型提出来的。我们知道，普通高斯模型对实际数据拟合效果还不错，但是其有一个致命的缺陷，就是其为单峰函数，如果数据的真实分布为复杂的多峰分布，那么单峰高斯的拟合效果就不够好了。

　　与单峰高斯模型不同，GMM模型是多个高斯模型的加权和，具体一点就是：

　　　　　　　　　　　　$p(\mathbf{x})\ =\ \sum_k\pi_k\mathcal{N}(\mathbf{x}|\mu_k,\Sigma_k)$　　

　　这是一个多峰分布，理论上，只要k足够大，GMM模型能拟合任何分布。

2. 困难

　　GMM模型比普通高斯模型拟合能力更强了，但是对其训练的难度也增加了。回忆一下，在训练普通高斯模型时，我们是对其分布函数去ln进行求导，具体一点就是：

　　　　　　　　　　　　$\frac{\partial lnp(\mathbf{x})}{\partial \mathbf{\theta}}\ =\ 0$

　　那么对于普通高斯函数来说，$lnp(\mathbf{x}) = C - \frac{1}{2}(\mathbf{x}-\mu)^T\Sigma^{-1}(\mathbf{x}-\mu)$，可以看到，ln将分布函数中的指数形式消除了，那么对其求导很容易得到闭式解。但是对于GMM模型来说就不是这么简单了。我们可以计算一下，其概率函数取ln形式为：

　　　　　　　　　　　　$lnp(\mathbf{x}) = ln\{ \sum_k\pi_k\mathcal{N}(\mathbf{x}|\mu_k,\Sigma_k)\}$

　　我们可以看到，因为在ln里面还有加法，所以其无法消除其中的指数形式，导致其最优化问题没有闭式解。所以想要用calculus的方式来解决GMM模型训练的问题是不行的。

3. Inspiration from k-means algorithm

　　没有什么事情是一步解决不了的，如果有，那就用两步。

　　　　　　　　　　　　　　　　　　　　　　　　--沃 · 兹基硕德

　　我们重新来看看GMM模型的表达式，其由多个高斯函数相加而成，你可以想想一个空间中有很多高斯函数，它们分别在各自中心点所在的位置。一个一维的三个高斯混合的模型示意如下：

　　　　　　　　　　

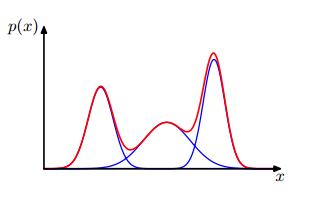
　　那么对于任何一个点，都有其最靠近的一个峰。比如在中间峰处的点，其概率几乎全是来自于第二个高斯分布。那么我们就可以这样想，是不是每个点都有其更加偏向的高斯峰呢？等等，这个想法好像在哪里见过？k-means算法中的第一步不就是干的这事吗？将每个点都分配给最近的一个类。但是，我们这里怎么去度量距离呢？继续使用点到中心的距离？这样好像把每个高斯的方差忽略掉了。那么既然是概率模型，最好的方法就是用概率来比较。对于一个点$\mathbf{x}$，第k个高斯对其的贡献为$\pi_k\mathcal{N}(\mathbf{x}|\mu_k,\Sigma_k)$，那么把$\mathbf{x}$分配给贡献最大的一个，这样看起来把各个因素考虑进去，似乎很合理了。

　　但是，我们发现，如果一个点处于两个峰之间呢，这样把其归为任何一个峰都不太好吧？当然，k-means也没有解决这个问题，但是我们这里是概率模型，我们有更好的描述方法，我们可以计算一个点$\mathbf{x}$属于每个高斯的概率。这样的考虑就比较全面了。那么点$\mathbf{x}$属于每个高斯的概率自然就取这个高斯对其的贡献$\pi_k\mathcal{N}(\mathbf{x}|\mu_k,\Sigma_k)$。为了使其成为一个概率，我们还需要对其归一化，所以得到第n个数据点属于第k个高斯的概率：

　　　　　　　　　　　　$\gamma_{nk}=\frac{\pi_k\mathcal{N}(\mathbf{x}_n|\mu_k,\Sigma_k)}{\sum_j\pi_j\mathcal{N}(\mathbf{x}_n|\mu_j,\Sigma_j)}$

　　按照k-means算法，第二步就是把$\gamma_{nk}$当做已知去做最优化。这里既然是要拟合分布，那么就使用最大似然的方法，最大化$lnp(\mathbf{X})$。那么这里就有一个问题了:在k-means算法中，目标函数是有$r_{nk}$这一项的，然而$lnp(\mathbf{X})$中并没有$\gamma_{nk}$这一项呀，我怎么把其当做已知的呢？这里我们不急，暂时不去管这个，我们先计算$\frac{\partial lnp(\mathbf{X})}{\partial \mu_k}$:

　　　　　　　　　　　　$\frac{\partial lnp(\mathbf{X})}{\partial \mu_k}\ =\ -\ \sum_n\frac{\pi_k\mathcal{N}(\mathbf{x}_n|\mu_k,\Sigma_k)}{\sum_j\pi_j\mathcal{N}(\mathbf{x}_n|\mu_j,\Sigma_k)}\Sigma_k(\mathbf{x}_n\ -\ \mu_k) $　　　　　　（1）

　　我们的$\gamma_{nk}$是不是已经出现了，那么上式可以简写为：

　　　　　　　　　　　　$\ -\ \sum_n\gamma_{nk}\Sigma_k(\mathbf{x}_n\ -\ \mu_k)$

　　令其等于0，可以得到：

　　　　　　　　　　　　$\mu_k\ =\ \frac{\sum_n\gamma_{nk}\mathbf{x}_n}{\sum_n\gamma_{nk}}$　　　　　　　　　　　　　　（2）

　　可以看到，其与k-means算法第二步中心点的计算方法$\mu_k=\frac{\sum_nr_{nk}\mathbf{x}_n}{\sum_nr_{nk}}$非常相似。

　　类似的，对$\Sigma_k$求导，可以得到：

　　　　　　　　　　　　$\Sigma_k\ =\ \frac{\sum_n\gamma_{nk}(\mathbf{x}_n-\mu_k)(\mathbf{x}_n-\mu_k)^T}{\sum_n\gamma_{nk}}$　　　　　　　　（3）

　　对$\pi_k$求导，可以得到：

　　　　　　　　　　　　$\pi_k\ =\ \frac{\sum_n\gamma_{nk}}{\sum_k\sum_n\gamma_{nk}}$ 　　　　　　　　　　　　　　（4）

　　自此，GMM训练方法就得到了，第一步，使用式（1）计算所有点的属于各个高斯的概率；第二步，利用式（2），（3），（4）更新均值、方差和权值。重复这两步直到收敛。

4. 与EM算法的关系

　　这里我们是从k-means算法出发得到的GMM训练算法，那么其与EM算法的关系与k-means算法和EM算法的关系类似。同样，我们后面可以看到，利用EM算法可以推导出GMM训练算法。