NOIP2024模拟12：孤帆远影

NOIP2024模拟12：孤帆远影

听了机房同学的讨论，于是T1死磕冒泡和逆序对做法。最后只得了40pts。

思想对了，但不是自己的做法。

还是要坚持自己想，坚持自己可以想出来，不要被任何人带偏。

T1

• 一句话题意：将一个已知序列通过不断“交换相邻位置”的操作调整成不严格单峰状态，问最小的操作次数。

• 有一种猜想是只要钦定了峰顶的位置，那么左右两边是不会交叉的。

  • 但这个猜想是错误的，它的证伪可以通过正解来理解

• 正解：假设题目要求我们调成升序，那么答案就是逆序对的数量。

• 现在是什么呢？要求前半段升序后半段降序。

• 那就分开逆序对！

• 具体来说，对于第 \(i\) 个数，想要待在左区间, 就必须穿过左边比它大的每个数,即在它左边的逆序对数量,待在右区间同理.

• 由于峰顶的位置不做限制,所以我们只需要看每个数放左边移动步数少一点,还是放右边少一点,就行了.

• 用树状数组求逆序对即可,只不过是正着倒着各扫一遍.

• 所以此题我很早就陷入了一个误区:枚举峰顶的位置,想来这其实不是题目所求.把自己限制住了!

  • 下次考试应该先在草稿本上写出这个想法.尝试一段时间返回去检查自己的思想是不是除了问题的时候,就方便大胆地走出误区.

  时间复杂度 \(O(N log N)\)

  #include<bits/stdc++.h>
  #define F(i,l,r) for(int i(l);i<=r;++i)
  #define G(i,r,l) for(int i(r);i>=l;--i)
  #define int long long
  #define lowbit(x) (-x&x)
  using namespace std;
  using ll = long long;
  const int N=2e5+5;
  int n,pos=0,mx=0;
  ll L[N],R[N],ans=0;
  ll a[N],tr[N];
  void add(int x){
  	for(;x<=mx;x+=lowbit(x)) tr[x]++;
  }
  int ask(int x){
  	int res=0;
  	for(;x>=1;x-=lowbit(x)) res+=tr[x];
  	return res;
  }
  signed main(){
  	//freopen("inde.in","r",stdin);
  	//freopen("inde.out","w",stdout);
  	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
  	cin>>n;
  	F(i,1,n) cin>>a[i],mx=max(mx,a[i]);
  	F(i,1,n){
  		add(a[i]);
  		L[i]=i-ask(a[i]);
  	}memset(tr,0,sizeof(tr));
  	G(i,n,1){
  		add(a[i]);
  		R[i]=n-i+1-ask(a[i]);
  	}
  	F(i,1,n){//the fjx
  		ans+=min(L[i],R[i]);
  	}
  	cout<<ans;
  	return 0;
  }
  

T2

• 一句话题意：给定一个起点,你现在需要依次抵达 \(n\) 个目标区间,既可以亲自去,也可以请别人代劳,但花费都是起终点之间的距离(允许亲自走一半再代劳一半).问最少的花费.

• 有点儿抽象,还没有完全理解,尝试着解释一下:

• 记 \(f[i][j]\) 表示第 \(i\) 次游历最终到达 \(j\) 的最小花费.

  • 首先从 \(f[i-1]\) 继承dp值
  • 对于操作1: \(j\) 离 \([l_i,r_i]\) 的最近距离即为此部分贡献.
  • 对于操作2:用 \(f[i][j]+1\) 更新 \(f[i][j-1]\) 和 \(f[i][j+1]\)

• 最关键的一步:根据操作2,对于每个 \(i\), 将 \(f[i][j]\) 看成关于 \(j\) 的函数,则一定长这个样子:

  

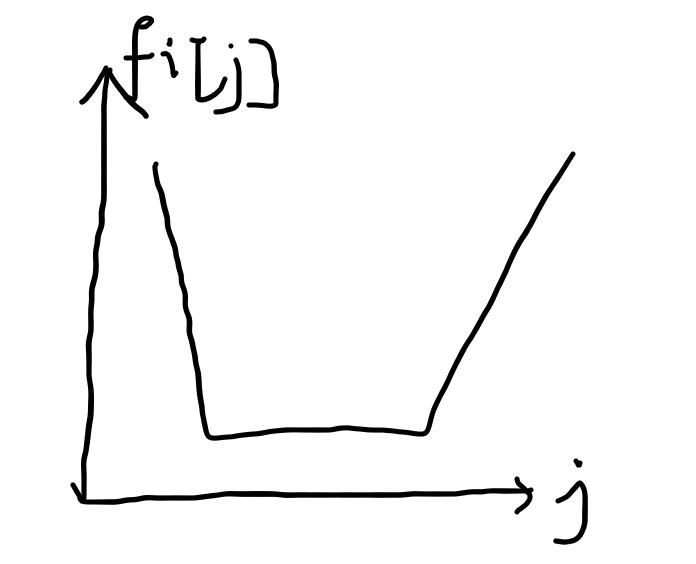
• 转移时,维护中间平的那一段,最后得到的贡献一定就是最优的.(感性理解一下)

• 时间复杂度 \(O(N)\)

  #include<bits/stdc++.h>
  #define F(i,l,r) for(int i(l);i<=r;++i)
  #define G(i,r,l) for(int i(r);i>=l;--i)
  #define int long long
  using namespace std;
  using ll = long long;
  const int N=5e5+105;
  int n,x;
  signed main(){
  //	freopen("festival.in","r",stdin);
  //	freopen("festival.out","w",stdout);
  	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
  	cin>>n>>x; int l=x,r=x,L,R;
  	ll ans=0;
  	while(n--){
  		cin>>L>>R;
  		if(l<=R && L<=r){
  			if(L>l) l=L;
  			if(R<r) r=R;
  		}
  		if(R<l) ans+=l-R,r=l,l=R;
  		if(L>r) ans+=L-r,l=r,r=L;
  	}
  	cout<<ans;
  	return 0;
  }
  

T3

• \(O(NlogN)\) 求\(LIS\) 的板题,只不过带了个系数而已.

• 理解:\(C_i\)的系数只影响后续 \(C_{i+1}\) 的判断,而不影响当前判断.

• 唯一的细节就是带系数之后的数不一定比原来小,要取 min.

  #include<bits/stdc++.h>
  #define F(i,l,r) for(int i(l);i<=r;++i)
  #define G(i,r,l) for(int i(r);i>=l;--i)
  #define lowbit(x) (-x&x)
  #define int long long
  using namespace std;
  using ll = long long;
  const int N=1e6+5;
  int f[N],a[N],b[N];
  int n;
  signed main(){
  	//freopen("geranium.in","r",stdin);
  	//freopen("geranium.out","w",stdout);
  	ios::sync_with_stdio(0); cin.tie(0); cout.tie(0);
  	cin>>n;
  	F(i,1,n) cin>>a[i];
  	F(i,1,n) cin>>b[i];
  	int ans=0;
  	F(i,1,n) f[i]=2e18;
  	F(i,1,n){
  		int pos=lower_bound(f+1,f+ans+1,a[i])-f;
  		f[pos]=min(f[pos],a[i]*b[pos]);
  		ans=max(ans,pos);
  	}
  	cout<<ans<<"\n";
  	return 0;
  }