hiho41 : 骨牌覆盖问题·一

原问题：骨牌覆盖问题

时间限制:10000ms

单点时限:1000ms

内存限制:256MB

描述

骨牌，一种古老的玩具。今天我们要研究的是骨牌的覆盖问题：
我们有一个2xN的长条形棋盘，然后用1x2的骨牌去覆盖整个棋盘。对于这个棋盘，一共有多少种不同的覆盖方法呢？
举个例子，对于长度为1到3的棋盘，我们有下面几种覆盖方式：

提示：骨牌覆盖

提示：如何快速计算结果

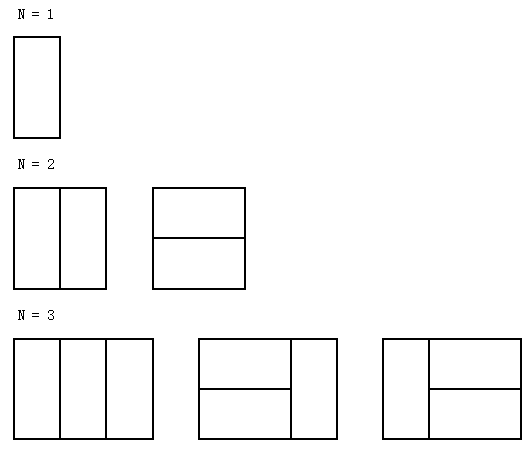
输入

第1行：1个整数N。表示棋盘长度。1≤N≤100,000,000

输出

第1行：1个整数，表示覆盖方案数 MOD 19999997

样例输入

62247088

样例输出

17748018

提示：骨牌覆盖

我们考虑在已经放置了部分骨牌(灰色)的情况下，下一步可以如何放置新的骨牌(蓝色)：

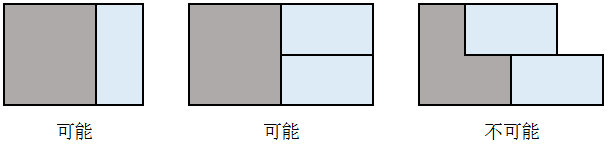
最右边的一种情况是不可能发生的，否则会始终多一个格子没有办法放置骨牌。或者说灰色部分的格子数为奇数，不可能通过1x2个骨牌放置出来。
那么通过对上面的观察，我们可以发现：
在任何一个放置方案最后，一定满足前面两种情况。而灰色的部分又正好对应了长度为N-1和N-2时的放置方案。由此，我们可以得到递推公式:
f[n] = f[n-1] + f[n-2];
这个公式是不是看上去很眼熟？没错，这正是我们的费波拉契数列。
f[0]=1,f[1]=1,f[2]=2,...

提示：如何快速计算结果

当N很小的时候，我们直接通过递推公式便可以计算。当N很大的时候，只要我们的电脑足够好，我们仍然可以直接通过递推公式来计算。
但是我们学算法的，总是这样直接枚举不是显得很Low么，所以我们要用一个好的算法来加速(装X)。
事实上，对于这种线性递推式，我们可以用矩阵乘法来求第n项。对于本题Fibonacci数列，我们希望找到一个2x2的矩阵M，使得(a, b) x M = (b, a+b)，其中(a, b)和(b, a+b)都是1x2的矩阵。
显然，只需要取M = [0, 1; 1, 1]就可以了：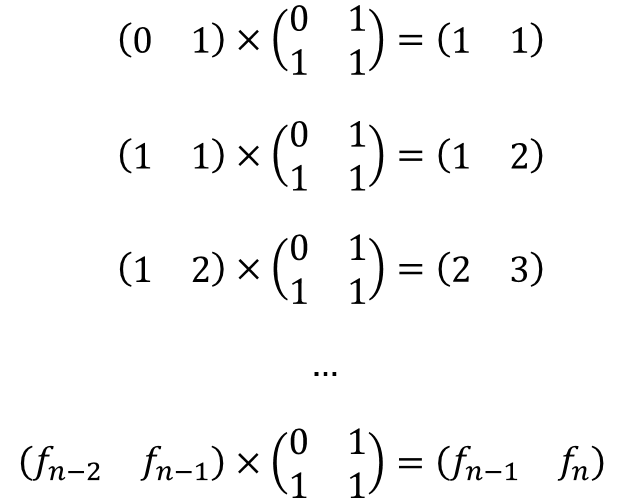

进一步得到：

那么接下来的问题是，能不能快速的计算出M^n？我们先来分析一下幂运算。由于乘法是满足结合律的，所以我们有：

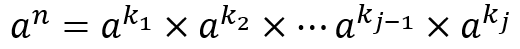
不妨将k[1]..k[j]划分的更好一点？

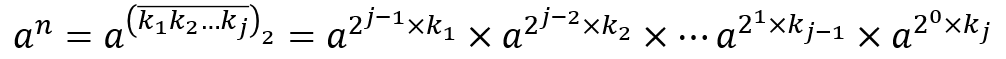
其中(k[1],k[2]...k[j])2表示将n表示成二进制数后每一位的数字。上面这个公式同时满足这样一个性质：

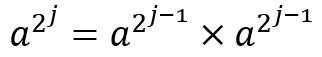
结合这两者我们可以得到一个算法：
1. 先计算出所有的{a^1, a^2, a^4 ... a^(2^j)}，因为该数列满足递推公式，时间复杂度为O(logN)
2. 将指数n二进制化，再利用公式将对应的a^j相乘计算出a^n，时间复杂度仍然为O(logN)
则总的时间复杂度为O(logN)
这种算法因为能够在很短时间内求出幂，我们称之为“快速幂”算法。

 #include <iostream>

 using namespace std;

 typedef long long ll;

 const int M = ;
 struct Matrix
 {
     int m[][];
     Matrix operator*(Matrix& a)
     {
         Matrix res;
         res.m[][] = ((ll)m[][]*a.m[][]+(ll)m[][]*a.m[][])%M;  // (ll)防止数据溢出
         res.m[][] = ((ll)m[][]*a.m[][]+(ll)m[][]*a.m[][])%M;
         res.m[][] = ((ll)m[][]*a.m[][]+(ll)m[][]*a.m[][])%M;
         res.m[][] = ((ll)m[][]*a.m[][]+(ll)m[][]*a.m[][])%M;
         return res;
     }
 };

 Matrix pow(Matrix m, int n)
 {
     Matrix res;
     if(==n)
         return m;
     res = pow(m, n/);
     if(n%==)
         res = res*res*m;
     else
         res = res*res;
     return res;
 }

 int main()
 {
     int N;
     cin>>N;

     Matrix mat;
     mat.m[][]=;
     mat.m[][]=;
     mat.m[][]=;
     mat.m[][]=;
     mat = pow(mat, N);

     cout<<mat.m[][];

     return ;
 }