HDU 5714

Problem Description

小明在旅游的路上看到了一条美丽的河，河上有许多船只，有的船只向左航行，有的船只向右航行。小明希望拍下这一美丽的风景，并且把尽可能多的船只都完整地拍到一张照片中。

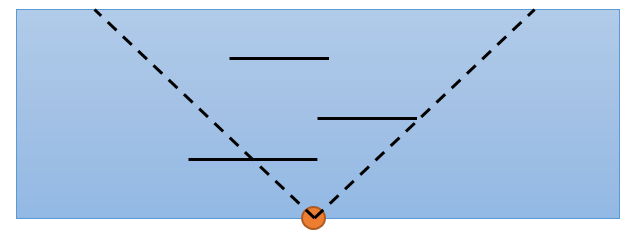
小明位于河的边上，并且可以在河边的任意位置进行拍照，照相机的视野恰好为90度角，只能以垂直于河边的方向进行拍照。河上的船只全都可看作是平行 于河边的一条线段，跟河边的距离各不相同，有的正在向左移动，有的正在向右移动，但移动速度恰好都是一样的。小明可以等待恰当的时间让尽量多的船只都走进 照相机的视野里，你不需要考虑船只之间会互相遮挡视野的情况。

Input

第一行为TTT，表示输入数据组数。

下面TTT组数据，对于每组数据：

第一行是一个数n(1≤n≤104)n(1\leq n\leq 10^{4})n(1≤n≤10​4​​)，表示船只的数量。

接下来nnn行，每行四个整数 x,y,z,d(−106≤x<y≤106,1≤z≤104)x,y,z,d(-10^{6}\leq x < y \leq 10^{6},1\leq z\leq 10^{4})x,y,z,d(−10​6​​≤x<y≤10​6​​,1≤z≤10​4​​)，表示船只的左端点位置、右端点位置、距离河边的距离，以及航行的方向。ddd为−1-1−1表示向左航行，111表示向右航行。

Output

对第iii组数据，输出

Case #i:

然后输出一行，仅包含一个整数，表示最多可以拍到多少完整的船只。

Sample Input

3
2
1 3 1 1
2 4 1 -1
2
1 3 1 -1
2 4 1 1
1
1 4 1 1

Sample Output

Case #1:
2
Case #2:
1
Case #3:
0

Solution:
考虑一条静止的船，容易求出在河岸上能完整拍到这条船的位置范围[L, R]，当这条船运动时，区间[L, R]也随之以相同的速度在河岸上移动。
考虑所有向左运动的船，它们对应的区间[L, R]是相对静止的,将这些区间的并看成一个整体，称为左点集；同理，所有向右运动的船对应的区间[L, R]的并也可看成一个整体，称为右点集，这两个点集（中的点）分别向左和向右运动。
我们假设相机固定在左点集中的某个点p,初始时刻右点集中在p左边(包括和p重合）的点，都必定会和p相遇。这样在p点所能（完整）拍到的最大船数就是，p点所能拍到的左行
的船数加上右点集中p左边(包括和p重合）的点上所能拍到的右行的船数的最大值。
实际上，我们没必要枚举左点集中的每一个点，只要枚举其中左行船对应的区间[L, R]的端点即可，换言之，可把左点集重定义成左行船对应的区间[L, R]的端点的集合。
右点集亦可做同样处理。

Implementation:
区间端点离散化，　差分序列

#include <cstdio>
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <algorithm>
using namespace std;
const int N(1e4+), M();
int a[*N], b[*N];

inline int id(int x){
    return x+M;
}

vector<int> c;
int x[N], y[N], z[N], d[N];

int main(){
    int T, n, m;
    int cs=;
    for(scanf("%d", &T); T--; ){
        scanf("%d", &n);
        printf("Case #%d:\n", ++cs);
        memset(a, , sizeof(a));
        memset(b, , sizeof(b));
        c.clear();
        for(int i=; i<n; i++){
            scanf("%d%d%d%d", x+i, y+i, z+i, d+i);
            int R=x[i]+z[i], L=y[i]-z[i];
            if(L>R) continue;
            c.push_back(R), c.push_back(L);
        }

        sort(c.begin(), c.end());
        int e=unique(c.begin(), c.end())-c.begin();

        for(int i=; i<n; i++){
            int R=x[i]+z[i], L=y[i]-z[i];
            if(L>R) continue;
            int id1=lower_bound(c.begin(), c.begin()+e, L)-c.begin();
            int id2=upper_bound(c.begin(), c.begin()+e, R)-c.begin();
            if(d[i]==-){
                a[id1]++;
                a[id2]--;
            }
            else{
                b[id1]++;
                b[id2]--;
            }
        }
        int ans=;
        for(int i=; i<e; i++)
            a[i]+=a[i-], b[i]+=b[i-];
        for(int i=; i<e; i++){
            b[i]=max(b[i], b[i-]);
        }
        for(int i=; i<e; i++)
            ans=max(ans, a[i]+b[i]);
        cout<<ans<<endl;
    }
    return ;
}