python 排序和查找算法

一、搜索

---

1.顺序查找

数据存储在具有线性或顺序关系的结构中时，可顺序访问查找

def sequential_search(ilist, item):
    pos = 0

    while pos < len(ilist):
        if ilist[pos] == item:
            return pos
        else:
            pos = pos + 1

    return -1

2.二分查找

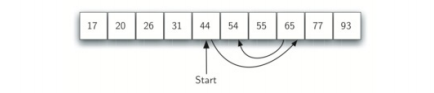
对于有序顺序表可使用二分查找，每次从中间项开始，故每次可以排除剩余项的一半

def binary_search(ilist, item):
    first = 0
    last = len(ilist)
    while first <= last:
        mid_point = (first + last) // 2
        if ilist[mid_point] == item:
            return mid_point
        else:
            if item < ilist[mid_point]:
                last = mid_point - 1
            else:
                first = mid_point + 1
    return -1

递归版本

def binary_search(ilist, item):
    if len(ilist) == 0:
        return -1
    else:
        midpoint = len(ilist) // 2
        if ilist[midpoint] == item:
            return midpoint
        else:
            if item < ilist[midpoint]:
                return binary_search(ilist[:midpoint-1], item)
            else:
                return binary_search(ilist[midpoint+1:], item)

3.Hash查找

数据存储在哈希表，哈希表每一个位置通常称为一个槽，槽一般可以从1开始依次编号，数据与槽之间的映射叫做hash 函数。负载因子

λ=占用的槽/表大小，如下表λ=6/11。搜索一个数只需要使用哈希函数计算数据的槽编号就可以查找到。

一些普通的hash函数：余数法（只需要将数据除以表大小）、分组求和法（将数据分成相等的大小的块，然后将块加在一起求出散列值）、平方取中法（先对数据平方，然后提取一部分数据结果）

由于槽数有限，所以会有冲突发生，解决冲突的方式：开放寻址（循环查看hash表，直到找到一个空槽），线性探测（顺序查找空槽，例如：1，2，3，4，5，缺点是容易产生聚集），重新散列（跳过槽，均匀分布冲突的槽，例如：1，3，5，7，9），二次探测（使用常量跳过值，如1，4，9，16），链表（如下图）

具体实现可以使用Python的字典

二、排序

---

1.冒泡排序

顾名思义，像泡沫一样浮起来，或者像重物一样沉底，每趟排序都会有一个极值到达最终位置。

def bubble_sort(nlist):
    for pass_num in range(len(nlist)-1, 0, -1):
        exchanges = False
        for i in range(pass_num):
            if nlist[i] > nlist[i+1]:
                exchanges = True
                nlist[i], nlist[i+1] = nlist[i+1], nlist[i]
        if not exchanges:
            return

2.选择排序

每一次选择一个极值放在最终位置。相比冒泡排序，减少了交换次数。

def selection_sort(nlist):
    for fill_slot in range(len(nlist)-1, 0, -1):
        position_of_max = 0
        for location in range(1, fill_slot+1):
            if nlist[location] > nlist[position_of_max]:
                position_of_max = location

        nlist[fill_slot], nlist[position_of_max] = nlist[position_of_max], nlist[fill_slot]

3.插入排序

类似于打牌抽牌时的插牌，逐次增加有序列表的个数。

def insertion_sort(nlist):
    for index in range(1, len(nlist)):
        current_value = nlist[index]
        position = index
        while position > 0 and nlist[position-1] > current_value:
            nlist[position] = nlist[position-1]
            position = position - 1
        nlist[position] = current_value

4.希尔排序

希尔排序通过将原始列表分解为多个较小的子列表来改进插入排序，每个子列表使用插入排序进行排序。

def shell_sort(nlist):
    sub_list_count = len(nlist) // 2
    while sub_list_count > 0:
        for start_position in range(sub_list_count):
            gap_insertion_sort(nlist, start_position, sub_list_count)
        sub_list_count = sub_list_count // 2

def gap_insertion_sort(nlist, start, gap):
    for i in range(start + gap, len(nlist), gap):
        current_value = nlist[i]
        position = i
        while position >= gap and nlist[position - gap] > current_value:
            nlist[position] = nlist[position - gap]
            position = position - gap

        nlist[position] = current_value

5.归并排序

一种递归算法，不断将列表分成一半，然后排序子列表，再合并。分而治之策略。

def merge_sort(nlist):
    if len(nlist) > 1:
        mid = len(nlist) // 2
        left_half = nlist[:mid]
        right_half = nlist[mid:]
        merge_sort(left_half)
        merge_sort(right_half)
        i, j, k = 0, 0, 0
        while i < len(left_half) and j < len(right_half):
            if left_half[i] < right_half[j]:
                nlist[k] = left_half[i]
                i += 1
            else:
                nlist[k] = right_half[j]
                j += 1
            k += 1
        while i < len(left_half):
            nlist[k] = left_half[i]
            i += 1
            k += 1
        while j < len(right_half):
            nlist[k] = right_half[j]
            j += 1
            k += 1

6.快速排序

选择一个值作为枢轴值，然后作为基准，序列变为一边比值大一边比值小的两部分，每趟排序确定枢轴值的位置。

def quick_sort(nlist):
    quick_sort_helper(nlist, 0, len(nlist) - 1)

def quick_sort_helper(nlist, first, last):
    if first < last:
        split_point = partition(nlist, first, last)
        quick_sort_helper(nlist, first, split_point - 1)
        quick_sort_helper(nlist, split_point + 1, last)

def partition(nlist, first, last):
    pivot_value = nlist[first]
    left_mark = first + 1
    right_mark = last
    while True:
        while left_mark <= right_mark and nlist[left_mark] <= pivot_value:
            left_mark = left_mark + 1
        while right_mark >= left_mark and nlist[right_mark] >= pivot_value:
            right_mark = right_mark - 1
        if right_mark < left_mark:
            break
        else:
            nlist[left_mark], nlist[right_mark] = nlist[right_mark], nlist[left_mark]
    nlist[first], nlist[right_mark] = nlist[right_mark], nlist[first]

    return right_mark

最后：