【题解】长度为素数的路径个数-C++

Description

对于正整数n (3≤n<20)，可以画出n阶的回形矩阵。下面画出的分别是3阶的，4阶的和7阶的回形矩阵：



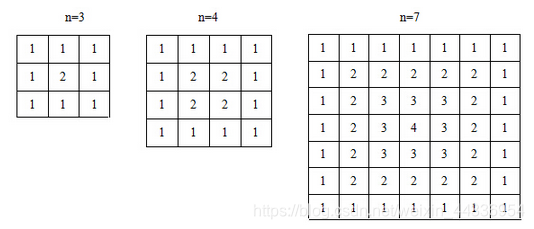
对于n阶回形矩阵，从左上角出发，每步可以向右或向下走一格，走2* n－2步，可以到达右下角。我们把这样的路

径上所有格子中的数值之和，叫做该路径的长度。本题要求，对于给出n值，求出n阶回形矩阵有多少路径的长度为

素数?如n=3时，路径及长度有：



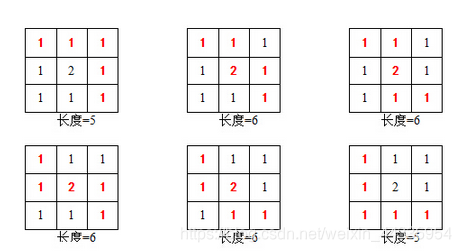
因此说，3阶回形矩阵有2条路径的长度为素数。

Input

一个自然数n (3≤n<20，不必判错)。

Output

一个正整数，即n阶回形矩阵中长度为素数的路径的个数。

Sample Input

3

Sample Output

2

这道题目第一个难点在于构造回形矩阵。

说是回形矩阵，我们可以想象成一个nn的矩阵叠加(n-1)(n-1)的矩阵…然后就可以叠加成为一个回形矩阵，但是需要判断n的奇偶性。。。build函数如下：

void build(int s1,int n1)
{
	if(s1==n1)
	{
		mp[s1][n1]=s1;
		return;
	}
	else if(s1>n1)return;
	for(int i=s1;i<=n1;i++)
	{
		for(int j=s1;j<=n1;j++)
		{
			mp[i][j]=s1;
		}
	}
	build(s1+1,n1-1);
	return;
}

顺便写出判断路径长度是否是质数的函数。。。

bool IsPrime/*这绝逼是我自己打的*/(int num)
{
	 if(num==1)
		return 0;
     if(num==2||num==3)
        return 1;
     if(num%6!=1&&num%6!=5)
        return 0;
     int tmp=sqrt(num);
     for(int i=5;i<=tmp;i+=6)
        if(num%i==0||num%(i+2)==0)
           return 0;
     return 1;
}

不懂的去翻我博客，有一篇专门讲这个的。

然后主要是搜索过程。

每个状态最多有两个拓展可能：

往右或往下，只要不出界，矩阵随便跑

然后注意判断是否出界就可以了，总体还不算难

#include<bits/stdc++.h>
using namespace std;
int n,mp[220][220],ans;
bool IsPrime/*这绝逼是我自己打的*/(int num)
{
	 if(num==1)
		return 0;
     if(num==2||num==3)
        return 1;
     if(num%6!=1&&num%6!=5)
        return 0;
     int tmp=sqrt(num);
     for(int i=5;i<=tmp;i+=6)
        if(num%i==0||num%(i+2)==0)
           return 0;
     return 1;
}
void build(int s1,int n1)
{
	if(s1==n1)
	{
		mp[s1][n1]=s1;
		return;
	}
	else if(s1>n1)return;
	for(int i=s1;i<=n1;i++)
	{
		for(int j=s1;j<=n1;j++)
		{
			mp[i][j]=s1;
		}
	}
	build(s1+1,n1-1);
	return;
}
void dfs(int x,int y,int cnt)
{
	if(x==n&&y==n)
	{
		if(IsPrime(cnt))
		{
			ans++;
		}
		return;
	}
	if(x<n)
	{
		cnt+=mp[x+1][y];
		dfs(x+1,y,cnt);
		cnt-=mp[x+1][y];
	}
	if(y<n)
	{
		cnt+=mp[x][y+1];
		dfs(x,y+1,cnt);
		cnt-=mp[x][y+1];
	}
	return;
}
int main()
{
	cin>>n;
	build(1,n);
	dfs(1,1,1);
	cout<<ans<<endl;
}

ov.